2022-10-09:我们给出了一个(轴对齐的)二维矩形列表 rectangles 。 对于 rectangle[i] = [x1, y1, x2, y2],其中(x1,y1)是矩形 i 左下角的坐
Posted 福大大架构师每日一题
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2022-10-09:我们给出了一个(轴对齐的)二维矩形列表 rectangles 。 对于 rectangle[i] = [x1, y1, x2, y2],其中(x1,y1)是矩形 i 左下角的坐相关的知识,希望对你有一定的参考价值。
2022-10-09:我们给出了一个(轴对齐的)二维矩形列表 rectangles 。
对于 rectangle[i] = [x1, y1, x2, y2],其中(x1,y1)是矩形 i 左下角的坐标
(xi1, yi1) 是该矩形 左下角 的坐标, (xi2, yi2) 是该矩形 右上角 的坐标。
计算平面中所有 rectangles 所覆盖的 总面积 。
任何被两个或多个矩形覆盖的区域应只计算 一次 。
返回 总面积 。因为答案可能太大,返回 10^9 + 7 的 模 。
输入:rectangles = [[0,0,2,2],[1,0,2,3],[1,0,3,1]]。
输出:6。
答案2022-10-09:
线段树模板题。一个矩形两个事件。这道题用了树结构,对于rust有点复杂,用了Rc<RefCell>的数据类型。
力扣850上测试,rust语言占用内存最低,go语言占用内存略高于rust,但运行速度最快。
不管怎么说,rust和go都是要优于java的。用java的人们,你们赶紧换语言,java过时了。
java,go,rust运行情况见截图。
代码用rust编写。代码如下:
use std::cell::RefCell;
use std::iter::repeat;
use std::rc::Rc;
impl Solution
pub fn rectangle_area(rectangles: Vec<Vec<i32>>) -> i32
let n = rectangles.len() as i32;
let mut arr: Vec<Vec<i64>> = repeat(repeat(0).take(4).collect())
.take((n << 1) as usize)
.collect();
let mut max: i64 = 0;
for i in 0..n
// x1 y1 左下角点的坐标
// x2 y2 右上角点的坐标
// 解释一下y1为啥要+1
// 比如y1 = 3, y2 = 7
// 实际的处理的时候,真实的线段认为是闭区间[4,7]的
// 如果不这么处理会有问题
// 比如先在y1 = 3, y2 = 7上,都+1
// 那么此时:
// value: 0 0 1 1 1 1 1 0
// index: 1 2 3 4 5 6 7 8
// 这是不对的!
// 因为线段[3,7]长度是4啊!而在线段树里,是5个1!
// 所以,y1 = 3, y2 = 7
// 我们就是认为是4~7,都+1
// 那么此时:
// value: 0 0 0 1 1 1 1 0
// index: 1 2 3 4 5 6 7 8
// 线段树上,正好4个1,和我们想要的距离是一致的
let x1 = rectangles[i as usize][0];
let y1 = rectangles[i as usize][1] + 1;
let x2 = rectangles[i as usize][2];
let y2 = rectangles[i as usize][3];
arr[i as usize][0] = x1 as i64;
arr[i as usize][1] = y1 as i64;
arr[i as usize][2] = y2 as i64;
arr[i as usize][3] = 1;
arr[(i + n) as usize][0] = x2 as i64;
arr[(i + n) as usize][1] = y1 as i64;
arr[(i + n) as usize][2] = y2 as i64;
arr[(i + n) as usize][3] = -1;
max = get_max(max, y2 as i64);
return cover_area(&mut arr, n << 1, max);
fn get_max<T: Clone + Copy + std::cmp::PartialOrd>(a: T, b: T) -> T
if a > b
a
else
b
fn cover_area(arr: &mut Vec<Vec<i64>>, n: i32, max: i64) -> i32
// 所有的事件,都在arr里
// [x, y1, y2, +1/-1]
// 早 -> 晚
//Arrays.sort(arr, 0, n, (a, b) -> a[0] <= b[0] ? -1 : 1);
arr[0..n as usize].sort_by(|a, b|
if a[0] < b[0]
std::cmp::Ordering::Less
else
std::cmp::Ordering::Greater
);
// max y的值,可能的最大值,非常大也支持!
let mut dst = DynamicSegmentTree::new(max);
let mut pre_x: i64 = 0;
let mut ans: i64 = 0;
for i in 0..n
// dst.query() : 开点线段树告诉你!y方向真实的长度!
ans += dst.query() * (arr[i as usize][0] - pre_x);
ans %= 1000000007;
pre_x = arr[i as usize][0];
dst.add(arr[i as usize][1], arr[i as usize][2], arr[i as usize][3]);
return ans as i32;
struct Node
cover: i64,
len: i64,
left: Option<Rc<RefCell<Node>>>,
right: Option<Rc<RefCell<Node>>>,
impl Node
fn new() -> Self
Self
cover: 0,
len: 0,
left: Option::None,
right: Option::None,
struct DynamicSegmentTree
root: Rc<RefCell<Node>>,
size: i64,
impl DynamicSegmentTree
fn new(max: i64) -> Self
Self
root: Rc::new(RefCell::new(Node::new())),
size: max,
pub fn add(&mut self, ll: i64, rr: i64, cover: i64)
self.add0(Rc::clone(&self.root), 1, self.size, ll, rr, cover);
fn add0(&mut self, cur: Rc<RefCell<Node>>, l: i64, r: i64, ll: i64, rr: i64, cover: i64)
if ll <= l && rr >= r
cur.as_ref().borrow_mut().cover += cover;
else
if cur.as_ref().borrow().left.is_none()
cur.as_ref().borrow_mut().left = Some(Rc::new(RefCell::new(Node::new())));
if cur.as_ref().borrow().right.is_none()
cur.as_ref().borrow_mut().right = Some(Rc::new(RefCell::new(Node::new())));
let m: i64 = l + ((r - l) >> 1);
if ll <= m
self.add0(
Rc::clone(&cur.as_ref().borrow().left.as_ref().unwrap()),
l,
m,
ll,
rr,
cover,
);
if rr > m
self.add0(
Rc::clone(&cur.as_ref().borrow().right.as_ref().unwrap()),
m + 1,
r,
ll,
rr,
cover,
);
self.push_up(cur, l, r);
fn push_up(&mut self, cur: Rc<RefCell<Node>>, l: i64, r: i64)
if cur.as_ref().borrow().cover > 0
cur.as_ref().borrow_mut().len = r - l + 1;
else
cur.as_ref().borrow_mut().len = if !cur.as_ref().borrow().left.is_none()
cur.as_ref()
.borrow_mut()
.left
.as_mut()
.unwrap()
.as_ref()
.borrow()
.len
else
0
+ if !cur.as_ref().borrow().right.is_none()
cur.as_ref()
.borrow_mut()
.right
.as_mut()
.unwrap()
.as_ref()
.borrow()
.len
else
0
;
pub fn query(&mut self) -> i64
return self.root.as_ref().borrow().len;
fn main()
let rectangles = vec![vec![0, 0, 2, 2], vec![1, 0, 2, 3], vec![1, 0, 3, 1]];
let ans = Solution::rectangle_area(rectangles);
println!("ans = :?", ans);
struct Solution
执行结果如下:
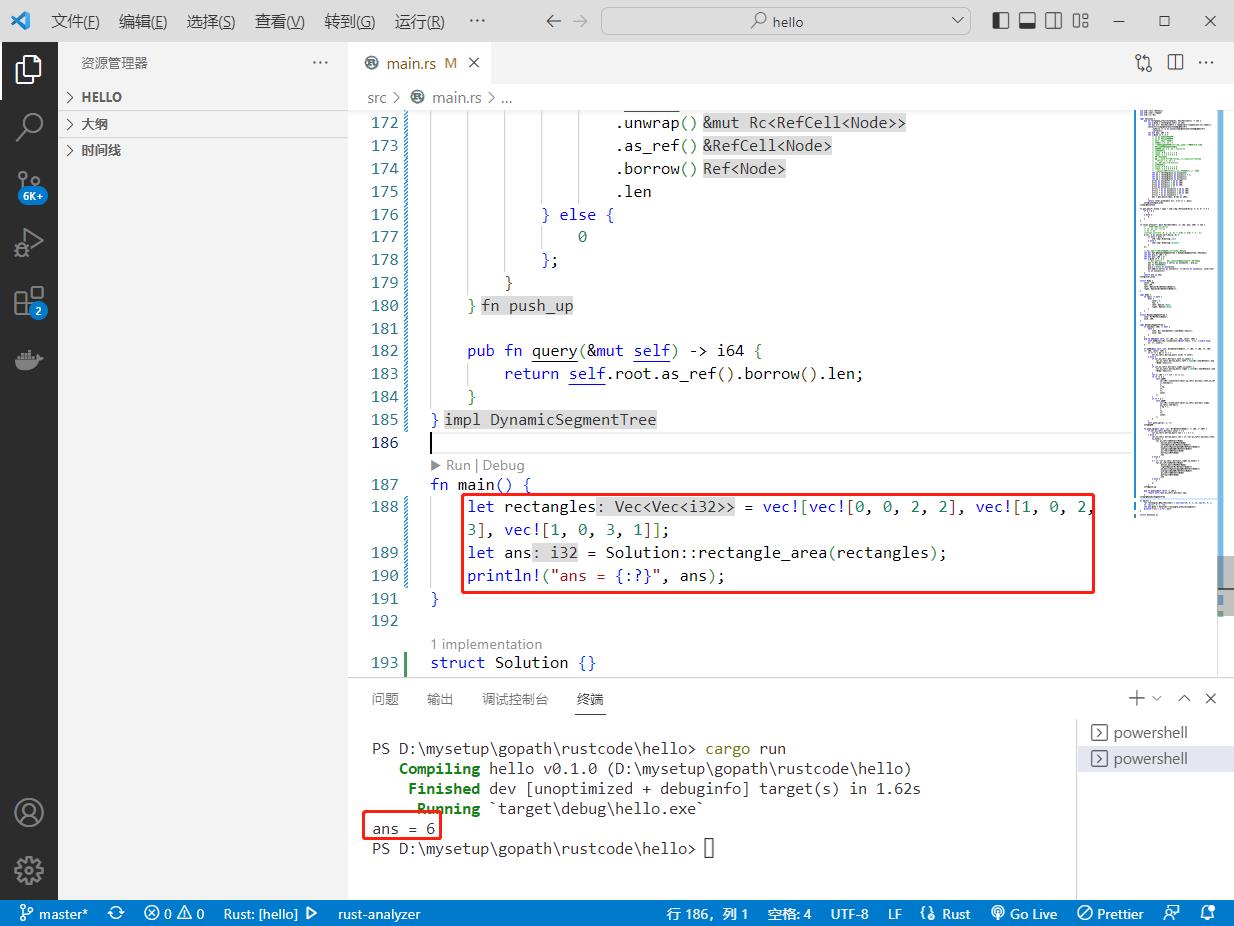
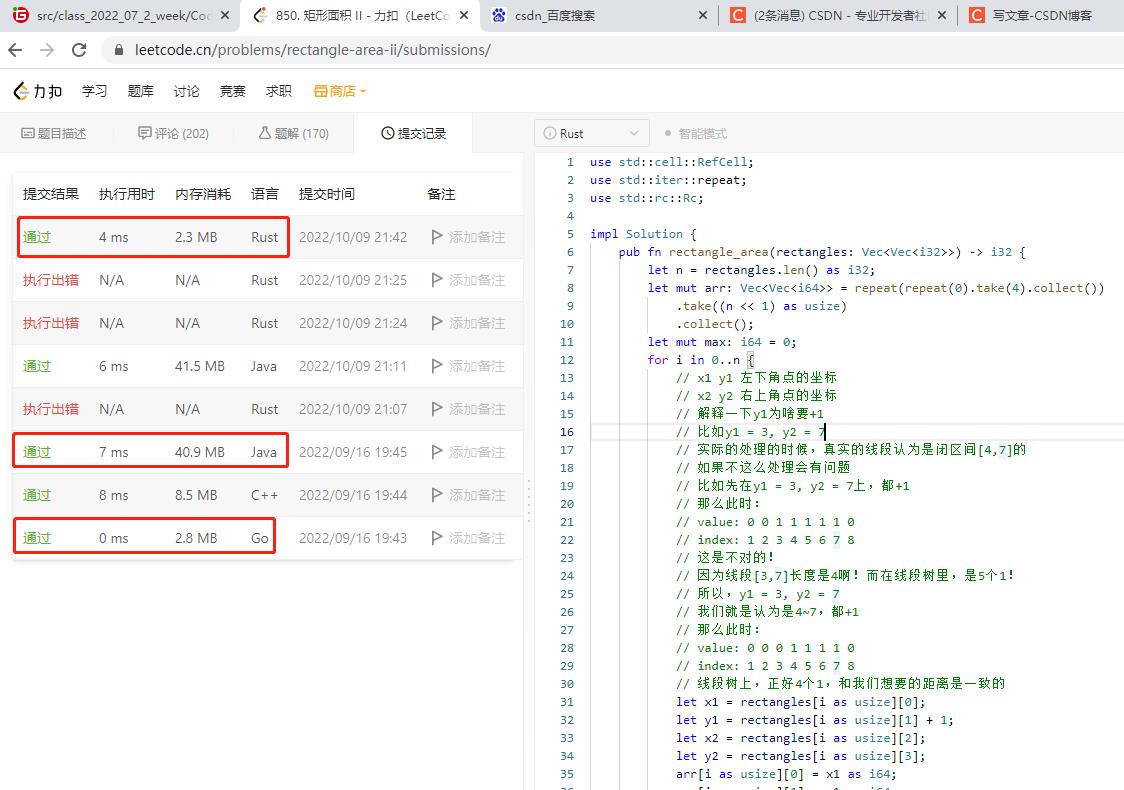
以上是关于2022-10-09:我们给出了一个(轴对齐的)二维矩形列表 rectangles 。 对于 rectangle[i] = [x1, y1, x2, y2],其中(x1,y1)是矩形 i 左下角的坐的主要内容,如果未能解决你的问题,请参考以下文章