回归与时间序列分析

Posted 2022-10-10 彭祥.

这篇博客是记录在数据挖掘中的回归与时间序列分析的学习过程

基础概念

回归分析应用

回归分析是一种应用极为广泛的数量分析方法。它用于分析事物之间的统计关系，侧重考察变量之间的数量变化规律，并通过回归方程的形式描述和反映这种关系，以帮助人们准确把握变量受其他一个或多个变量影响的程度，进而预测提供科学依据。
在大数据分析中，回归分析是一种预测性的建模技术，它研究的是因变量(目标)和自变量(预测器)之间的关系。这种技术通常用于预测分析、时间序列模型，以及发现变量之间的因果关系。

相关关系与函数关系

回归分析是处理多变量间相关关系的一种数学方法。相关关系不同于函数关系，后者反映变量之间的严格依存性，而前者则表现出一定程度的波动性或随机性，对自变量的每一个取值，因变量可以有多个数值与之相对应。
当自变量为非随机变量而因变量为随机变量时，它们的关系分析成为回归分析；当两者都是随机变量时，它们的关系分析成为相关分析。

回归分析的分类

回归分析包含线性回归与非线性回归，其中线性回归又包含简单线性回归和多元线性回归。下面是简单介绍：

简单线性回归分析

线性回归分析中，如果仅有一个自变量于一个因变量，且关系大致上可用一条直线表示，则称之为简单线性回归分析。
如果发现因变量Y和自变量X之间存在高度的正相关，则可以确定一条直线方程，使得所有的数据点尽可能接近这条拟合的直线。简单线性回归分析的模型可以用以下方程表示：

Y = a + b x

其中，Y为因变量，a为截距，b为相关系数，x为自变量。
多元线性回归分析
多元线性回归分析是简单线性回归分析的推广，指的是多个因变量对多个自变量的回归分析。其中最常用的是只限于一个因变量但有多个自变量的情况，也叫多重回归分析。多重回归分析的一般形式如下：

非线性回归数据分析

对于线性回归问题，样本点落在空间中的一条直线上或该直线的附近，因此可以使用一个线性函数表示自变量和因变量间的对应关系。然而在一些应用中，变量间的关系呈现曲线形式，因此无法用线性函数表示自变量和因变量间的对应关系，而需要使用非线性函数表示。
数据挖掘中常用的一些非线性回归模型：

二次曲线模型： Y=a+b₁​ X+b ₂ X²
双曲线模型： Y=a+ X/b

由于许多非线性模型是等价的，所以模型的参数化不是唯一的，这使得非线性模型的拟合和解释相比线性模型复杂得多。在非线性回归分析中估算回归参数的最通用的方法依然是最小二乘法（因为在线性回归分析中估算回归参数使用的也是最小二乘法）。

最小二乘法

最小二乘法是我们进行回归分析中估算参数的最常用的方法：
我们首先以简单的一元线性回归为例：

一元线性回归求解过程

多元线性回归分析求解过程

多元线性回归分析求解则可以借助线性代数来解决

注意：以上是在假设X^TX存在可逆阵的情况下，因为是线性多元，所以必定满足。

非线性回归求解过程

对于非线性的回归求解有两种方式，一种还是我们利用矩阵向量推导的公式进行回归分析，另一种则是通过迭代法，我们常使用的迭代方法即为梯度下降。
线性最小二乘的解是closed-form即有可逆阵 ，而非线性最小二乘没有closed-form（即 没有可逆矩阵），通常用迭代法求解。

向量矩阵形式求参数

在X^TX存在可逆阵情况下可以使用该方法：

同时我们可以使用程序来实现拟合过程：

import numpy as np
import matplotlib.pyplot as plt
import numpy.linalg as lg
t = np.arange(1, 17, 1)
y = np.array([4, 6.4, 8, 8.8, 9.22, 9.5, 9.7, 9.86, 10, 10.20, 10.32, 10.42, 10.5, 10.55, 10.58, 10.6])
plt.figure()
plt.plot(t, y, 'k*')
# y=at^2+bt+c
A = np.c_[t ** 2, t, np.ones(t.shape)]
w = lg.inv(A.T.dot(A)).dot(A.T).dot(y)
plt.plot(t, w[0] * t ** 2 + w[1] * t + w[2])
plt.show()

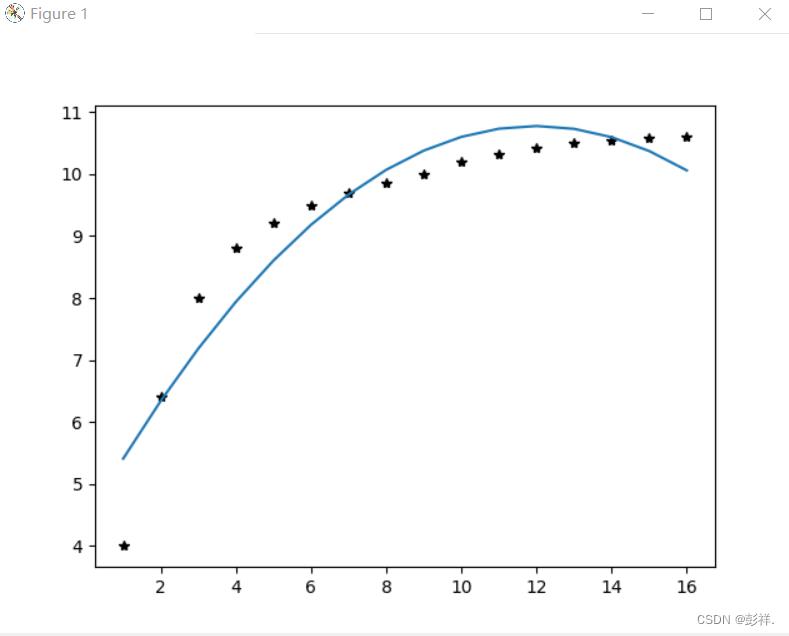
迭代法求解回归分析问题

迭代法，即在每一步update未知量逐渐逼近解，可以用于各种各样的问题（包括最小二乘），比如求的不是误差的最小平方和而是最小立方和。
梯度下降是迭代法的一种，可以用于求解最小二乘问题（线性和非线性都可以）

回归分析解决的问题

回归分析是研究变量间函数关系的一种方法。变量之间的关系可以表示为方程的形式。
其能够进行因素分析，确定影响某一变量的若干变量（因素）中，何者为主要，何者为次要，以及它们之间的关系，比如研究房屋面积与价格，或者考虑更多因素影响价格的情况。