每日一读Towards Understanding the Instability of Network Embedding

Posted 2022-10-05 海轰Pro

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了每日一读Towards Understanding the Instability of Network Embedding相关的知识，希望对你有一定的参考价值。

简介

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～

ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！

唯有努力💪

【每日一读】每天浅读一篇论文，了解专业前沿知识，培养阅读习惯（阅读记录仅供参考）

论文简介

原文链接：https://ieeexplore.ieee.org/document/9076342

期刊：IEEE Transactions on Knowledge and Data Engineering ( Volume: 34, Issue: 2, 01 February 2022) （CCF A类）

年度：2022年2月1日（发表日期）

Abstract

网络嵌入算法学习从节点的离散表示到保持节点邻近性的连续向量空间的映射

这些技术在节点分类、链路预测和网络对齐等各种下游任务中具有广泛的应用

尽管最近在设计新模型方面做出了努力，但很少有人注意理解网络嵌入的不稳定性

在本文中，我们通过研究几种最先进的网络嵌入方法来填补这一空白

节点嵌入在潜在空间中形成几何形状

表征几何对于找出网络嵌入的方差至关重要

因此，我们定义了两个度量来表征几何属性，并发现节点嵌入在嵌入空间的不同实例中会颤抖

然后，我们正式将节点嵌入的稳定性定义为节点最近邻居的不变性

实验结果表明，现有的嵌入方法具有很大的不稳定性

我们探索了影响不同方法稳定性的影响因素，发现网络结构和算法模型都显着影响节点嵌入的稳定性

最后，我们检查了嵌入不稳定性对下游任务的影响，并发现了对性能的显着影响。

1 INTRODUCTION

图形对于表示网络系统（如社会、生物和通信网络）至关重要 [1]、[2]、[3]。图的离散性极大地促进了许多复杂系统的分析。然而，大多数现有的离散算法都存在计算成本高的问题。此外，设计和实现并行和分布式替代方案通常具有挑战性 [4]、[5]。此外，图在推广许多基于连续特征的机器学习算法时也面临困境。为了解决这些问题，研究人员开发了许多有用的嵌入算法来学习节点的向量表示，从而保持节点的邻近性 [6]。已经验证，DeepWalk [7]、Node2vec [8] 和 Struc2vec [9] 等嵌入方法在节点分类 [10]、链接预测 [11] 和网络对齐 [12] 等各种下游任务中很有用.在本文中，我们交替使用术语“网络”和“图”、“节点”和“顶点”、“边”和“链接”。

网络嵌入算法通常包括两个主要步骤，包括节点邻近度估计和低维表示学习。由于准确计算节点接近度极其困难或不可能，许多现有算法利用随机游走和负抽样等抽样方案来提高有效性和效率[7]、[8]、[9]、[13]。一些基于深度神经网络的方法采用随机优化，例如随机梯度下降方案来提高计算效率 [14]、[15]。所有这些方法都不可避免地在学习向量中引入了一些方差。也就是说，我们在嵌入方法的不同实例中获得了不一致的结果。实例化意味着我们将算法应用于特定网络并获得为下游任务做好准备的嵌入向量。

网络嵌入的许多应用都围绕潜在空间中最近邻的计算[16]。实验结果表明，节点嵌入的方差会导致最近邻的显着波动，这可能会影响网络嵌入在下游任务中的性能。这一观察表明这些方法具有大量的不稳定性。揭示不稳定性的特征和影响因素对于网络嵌入算法的设计、解释和评估至关重要。例如，了解嵌入方差的原因可能有助于模型的可解释性，例如具有负样本的 Skip-Gram 模型 (SGNS) [7]、[8]、[13]、多层神经网络 [14] ]、[17] 和深度自动编码器网络 [15]。此外，这些模型的可解释性对于扩大其在许多对信心至关重要的场景中的应用至关重要，例如医疗、自动驾驶汽车和金融安全。尽管最近努力设计新模型，但很少有人关注对网络嵌入不稳定性的理解。我们承认设计一个有效的嵌入模型来克服不稳定性是至关重要的。然而，在本文中，我们专注于探索网络嵌入不稳定性的特征和原因及其对下游任务的影响。第 7 节讨论了稳定网络嵌入的可能性以及嵌入不稳定性理论分析的可能研究方向。

在理解网络嵌入不稳定性方面存在三个挑战

首先，节点嵌入在潜在空间中形成几何形状。我们必须设计适当的度量来表征节点嵌入的几何形状，这对于理解嵌入不稳定性至关重要
其次，我们必须定义一个合适的嵌入稳定性指标来反映下游任务的利用率，以使研究有意义
第三，影响网络嵌入稳定性的因素很多，不同的模型可能有不同的影响因素。因此，我们必须提出一种合适的方法来探索不同模型的影响因素。

在本文中，我们开发了一个测量框架来解决上述问题，并对网络嵌入不稳定性进行系统研究

图 1 展示了本研究的路线图

首先，我们研究了不同方法网络对的嵌入空间的几何特征
- 为了描述节点嵌入如何在潜在空间中分布，我们定义了两个指标，包括幅度和同心度，以表征节点嵌入的几何形状
- 我们还研究了嵌入方差如何影响几何。结果表明，每个节点点都在潜在空间的一个小区域内颤抖，并且不同的节点具有不同的方差量
- 此外，不同的方法具有不同的方差分布。这些观察表明，不同的嵌入模型具有不同的几何特征，节点嵌入的方差对几何有不同的影响。
其次，我们提出了网络嵌入稳定性的正式定义
- 节点嵌入的几何方差不能用作不稳定性测量的指标，因为它们不能反映下游任务的利用率
- 为了解决这个问题，我们将网络嵌入的不稳定性量化为不同嵌入空间中节点最近邻居的方差
- 我们测量了基于现实世界和人工网络的不同网络嵌入算法的不稳定性特征
- 发现不同的网络算法在不同的网络上具有不同的稳定性分布，说明网络结构和算法模型都会影响网络嵌入的稳定性。
最后，我们研究了影响嵌入稳定性的影响因素以及嵌入不稳定性对下游任务的影响
- 在本文中，我们考虑了两种内在因素，包括网络结构和算法模型
- 结果表明，节点和边数、平均节点度、网络密度和分类性等网络属性对不稳定性有显着影响
- 我们还评估了嵌入不稳定性对几个下游任务性能的影响，包括节点分类、链接预测和网络对齐。据了解，不稳定性对性能有显着影响。

我们这项工作的目的是了解网络嵌入的不稳定性及其对下游任务的影响，而不是比较不同算法的性能或寻求最小化嵌入不稳定性的方法。

2 R ELATED W ORK

这项研究的部分原因是最近发现自然语言处理（NLP）领域的词嵌入不稳定。词嵌入是将词映射到低维向量空间中的点 [18]、[19]、[20]。该技术已被用于各种 NLP 任务 [21]、[22]、[23]。最近的研究表明，不同嵌入空间中单词的最近邻居不一致，表明单词的嵌入具有很大的不稳定性[24]、[25]、[26]。安东尼亚克等人。 [24] 发现，对于各种词嵌入算法，嵌入空间中单词的距离对训练语料库中的微小变化高度敏感。 Pierrejean 和 Tanguy [25] 研究了用不同参数训练的最近邻词嵌入的变化。他们发现不同语义空间中的单词在不同嵌入空间中具有不同的最近邻。温德兰特等人。 [26] 研究了影响词嵌入不稳定性的因素，发现域和词性是两个关键因素。该研究还表明，词嵌入的不稳定性对下游任务的性能有重大影响。

与词嵌入相比，网络嵌入算法具有明显的不稳定性原因。例如，DeepWalk 采用随机游走模型来探索节点的关系信息 [7]。该模型在生成的节点上下文中引入了固有的方差，这进一步导致了节点嵌入的不稳定性。我们将现有方法大致分为三类，包括基于矩阵分解的方法、结构上下文推理模型和基于深度神经网络的方法 [27]、[28]。不同的方法及其变体在嵌入空间中具有不同的方差原因。

2.1 Matrix Factorization

基于矩阵分解 (MF) 的方法，例如 HOPE [29] 和 GraRep [30]，采用传统的矩阵分解方法，例如奇异值分解 (SVD) 来寻找网络的低维表示。例如，HOPE [29] 通过捕获节点之间的不对称传递性来保留大规模网络的高阶关系信息。 GraRep [30] 考虑邻接矩阵的幂以捕获节点之间的关系信息。给定相同的网络，由于矩阵分解的确定性，这些基于 MF 的方法总是产生相同的嵌入结果。这意味着这些方法对于静态网络是稳定的。然而，这些方法相对于网络结构的变化表现出显着的嵌入不稳定性。初步实验表明，基于 MF 的算法的稳定性比其他随机模型对网络结构的变化更敏感（见补充材料 S1，可在计算机协会数字图书馆 http://doi.ieeecomputer Society.org/10.1109/TKDE.2020.2989512）。在本文中，我们关注静态网络中的网络嵌入不稳定性问题。

2.2 Structural Context Inference

基于结构上下文推断的方法采用 Skipgram 模型来训练故意生成的节点结构上下文 [27]。 DeepWalk [7] 利用截断的随机游走来学习节点的结构上下文。生成的随机路径中节点的共现率编码了结构信息，例如节点的邻域关系。与 DeepWalk 不同，Node2vec [8] 还采用由两个附加参数 p 和 q 引导的有偏随机游走来生成节点的结构上下文。这两个附加参数允许搜索过程在广度优先采样 (BFS) 和深度优先采样 (DFS) 之间进行插值。 Struc2vec [9] 构建了一个多层图来编码不同尺度的结构相似性。基于构建的多层图执行随机游走以生成节点的结构上下文。所有这三种方法都利用 Skip-Gram 模型进行潜在表示学习。LINE [13] 基于节点之间的一阶和二阶关系信息优化精心设计的损失函数，以保留本地和全局网络结构。它采用边缘采样方案来提高推理效率和计算效率。这些方法不稳定的原因是双重的。首先，上下文生成模型，例如随机游走和边缘采样，会给推断的节点邻近度带来不确定性。其次，Skip-gram 模型采用的负采样方案将方差引入了嵌入空间。这些因素共同导致节点嵌入的不稳定性。

2.3 Deep Neural Network

基于深度神经网络的方法利用神经网络的非线性特性将原始离散空间转换为低维连续向量空间[27]。 SDNE（Structural Deep Network Embedding）[14]采用具有多层非线性函数的半监督深度模型来捕捉网络结构的隐藏信息。该方法联合利用一阶和二阶邻域来保存网络结构的局部和全局信息。DNGR（用于图表示的深度神经网络）[15]采用随机冲浪模型直接从图中捕获结构信息。它引入了一个堆叠的去噪自动编码器来提取复杂的特征并对网络嵌入的非线性进行建模。 SiNE [17] 是一个用于有符号网络的深度神经网络学习框架，它优化了由图论指导的目标函数。这些方法的方差是由随机梯度下降方案的采用、神经网络初始化的随机性以及局部优化的可能性共同造成的。

上述分析表明，节点嵌入在潜在空间中存在一定程度的不稳定性。然而，很少有人关注嵌入不稳定性的特征和原因的理解。在本文中，我们迈出了衡量最先进网络嵌入方法稳定性的第一步。

3 GEOMETRY OF NETWORK EMBEDDING

4 NETWORK EMBEDDING STABILITY

在本节中，我们首先根据其在下游任务中的利用率正式定义网络嵌入的稳定性。然后，我们描述了不同方法-网络对的稳定性分布。

4.1 Definition of Embedding Stability

许多网络嵌入应用程序，例如链接预测、节点分类、个性化图搜索和欺诈检测，直接围绕着计算与查询节点最“相似”的节点 [16]。其他图挖掘问题，例如节点聚类和网络对齐，也隐含地依赖于嵌入空间中最近邻的计算[35]。因此，我们将网络嵌入的稳定性定义为不同实例中节点最近邻居的不变性，这评估了嵌入方差对下游任务性能的可能影响

为了量化嵌入方法 M 的稳定性，我们将 M 应用于具有相同参数设置的网络 G T 次。这产生了一组嵌入空间，用 V 1/4 fX1 表示； X2; . . . ; XT 克。下游任务通常采用两种距离度量，包括余弦相似度和欧几里得距离，来检索节点的最近邻居 [36]。在本文中，我们报告了基于余弦相似度的结果。较高的相似度分数表明空间中的距离较近。我们基于欧几里德距离获得了类似的结果，并出于空间考虑将其省略。

7 DISCUSSION

7.1 Towards Stable Network Embedding

网络嵌入的两个阶段从根本上引入了不稳定性，包括节点邻近度估计和降维。一个合适的节点邻近度估计模型应该包括尽可能多的结构和属性信息。准确计算高阶结构邻近度通常具有挑战性，因为计算成本相对于节点邻近度的阶数迅速增加。因此，提出了许多可行的方法来估计采样方案的结构接近度，例如随机游走 [7]、[8] 和随机冲浪方法 [14]，它们在嵌入空间中引入了一些方差。因此，一个主要的研究方向是在不引入随机过程的情况下设计一种有效的节点邻近度计算方法。

最近，邱等人。 [49] 发现，DeepWalk、LINE、PTE 和 node2vec 等网络嵌入模型本质上是在执行隐式矩阵分解。基于这一观察，他们提出了一种矩阵分解框架NetMF，该框架避免了负采样和随机初始化等随机操作。因此，NetMF 实现了稳定的嵌入并提高了性能。然而，该算法在时间和空间方面都非常昂贵，因此无法用于大规模网络。为了解决这个问题，提出了 NetSMF 通过稀疏矩阵分解来提高计算效率 [50]。NetSMF 采用随机奇异值分解 (SVD) 进行高效的稀疏矩阵分解，在下游任务中牺牲了一些精度性能并引入了一些方差 [50]。张等人。 [51] 提出了一种基于 SVD 框架的任意阶邻近保留嵌入方法。他们提出了一种可扩展的分解解决方案来导出嵌入向量并在任意顺序的接近度之间移动它们。所提出的方法具有与网络大小有关的线性时间复杂度。上述分析表明，基于 SVD 的方法是生成稳定嵌入的可行方法。然而，必须设计新的方案来解决效率问题。

嵌入不稳定的另一个原因是优化方案，例如 Skip-Gram 模型中使用的负采样和深度神经网络在降维阶段使用的随机梯度下降方法。这些方法通过采用随机过程来提高计算效率，这会导致潜在空间的显着变化。正是计算效率和嵌入有效性之间的权衡导致了该阶段网络嵌入的不稳定性。一些研究人员提出通过向模型提供高质量的负样本来提高性能[52]、[53]、[54]。然而，这些方法仍然存在嵌入不稳定性，因为它们不会改变基础模型。

值得注意的是，最近的一些工作建议使用高斯分布作为节点的隐藏表示来增强节点嵌入的鲁棒性 [55]、[56]。均值向量表示节点在嵌入空间中的位置，方差项反映节点的不确定性。该模型捕获数据的不确定性，例如由于多方面的人类行为[56]，相邻节点之间可能存在的矛盾和不确定的边缘生成。这个想法也被用来保护图卷积网络免受对抗性攻击[57]。与这些工作不同，我们关注嵌入模型本身固有的不稳定性，即即使将相同的模型多次应用于相同的网络，也会得到不一致的结果。我们还检查了这些模型的稳定性，发现高斯嵌入模型也表现出大量的不稳定性。

一个出现的问题是基于网络结构扰动的网络嵌入模型的对抗性攻击[58]、[59]、[60]。 Z€ugner 等人。 [58] 已经表明，节点连接的对抗性扰动会显着降低基于神经网络的方法在节点分类的半监督任务中的准确性。一些研究人员提出使用对抗学习来提高网络嵌入的鲁棒性[61]。与这些工作相比，在静态网络的场景中研究了嵌入不稳定性问题，这比对抗性攻击问题更严格。对网络嵌入不稳定性的良好理解为评估漏洞和提高网络嵌入方法的鲁棒性提供了见解。

7.2 Directions of Theoretical Analysis

最近的研究发现，网络嵌入模型本质上是对邻近矩阵进行分解[62]：

其中 M 2 Rn n 是一些矩阵，包含由上下文推理模型（例如随机游走）估计的节点的邻近信息； X 2 Rn d 和 X0 2 Rd n 分别是嵌入矩阵和上下文矩阵； n 是节点数，d 是嵌入维数。这一观察为我们从理论上分析网络嵌入的不稳定性提供了一种可行的方法。形式上，由于随机游走的随机性，我们将基于随机游走的网络嵌入模型的邻近矩阵视为随机变量。将 M 表示为预期的邻近矩阵，然后

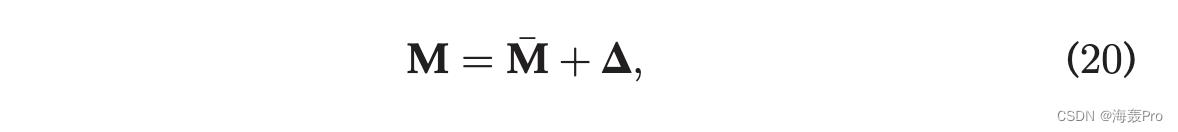
其中 D 表示由随机游走引起的扰动。评估 D 对特征值和特征向量的影响是分析节点嵌入不稳定性的一种很有前途的方法。该理论工具已被用于分析维度对嵌入质量的影响 [63]。此外，扰动特征对可以通过扰动矩阵 D [64]、[65] 的一阶有效地逼近，这为嵌入稳定性的理论分析提供了有力的工具。

邱等人。 [49] 已经导出了将 DeepWalk、LINE、PTE 和 node2vec 统一到矩阵分解框架中的邻近矩阵的封闭形式。例如，已经表明，DeepWalk 正在隐式分解一个随机矩阵，该矩阵在概率上收敛到一个移位的逐点互信息 (PMI) 矩阵 [49]。因此，我们可以正式制定预期的邻近矩阵 M。不幸的是，关于随机游走如何影响扰动矩阵 D，这仍然是一个悬而未决的问题，这是网络嵌入不稳定性理论分析的重要研究方向。

矩阵分解含义的一个重要副作用是嵌入被正交矩阵[64]任意旋转，而不影响目标：

其中 Q 2 Rd d 是任意正交矩阵，即 QTQ 1/4 I。由于嵌入不受约束，并且唯一的误差信号来自正交不变的目标，因此整个嵌入空间在训练期间可以任意旋转。然而，旋转方差没有问题，因为它不影响嵌入空间中节点的相对位置。