:无穷级数
Posted 码农爱德华
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了:无穷级数相关的知识,希望对你有一定的参考价值。
文章目录
Ch12. 无穷级数
(一) 常数项级数
正项级数
交错级数
任意项级数
4个特殊的常数项级数
①等比级数
②p级数
③调和级数
∑
n
=
1
∞
1
n
=
1
+
1
2
+
1
3
+
.
.
.
+
1
n
+
.
.
.
=
∞
\\sum\\limits_n=1^∞\\dfrac1n=1+\\dfrac12+\\dfrac13+...+\\dfrac1n+...=∞
n=1∑∞n1=1+21+31+...+n1+...=∞ 发散
④交错调和级数
交错调和级数:收敛
交错p级数:收敛
收敛级数的性质(针对任意项级数)
(1)(2)加减数乘都收敛
例题:06年9.

分析:ABC仅对正项级数成立。
举反例:
AB:
a
n
=
(
−
1
)
n
⋅
1
n
a_n=(-1)^n·\\dfrac1n
an=(−1)n⋅n1
C:
a
n
=
(
−
1
)
n
⋅
1
n
a_n=(-1)^n·\\dfrac1\\sqrtn
an=(−1)n⋅n1
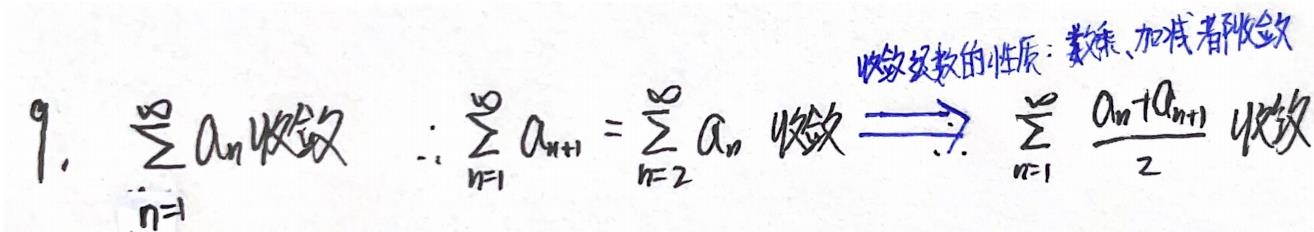
答案:D
常数项级数的审敛法
1.正项级数审敛法
①充要条件
②比较审敛法
大的收敛,小的收敛;
小的发散,大的发散。
例题:09年4. 正项级数的比较审敛法、举反例

分析:
对于A,取
a
n
=
b
n
=
(
−
1
)
n
1
n
a_n=b_n=(-1)^n\\dfrac1\\sqrtn
an=bn=(−1)nn1,则
a
n
b
n
=
1
n
a_nb_n=\\dfrac1n
anbn=n1,为调和级数,发散
对于C,用正项级数的比较审敛法证明C正确: lim n → ∞ a n 2 b n 2 ∣ b n ∣ = lim n → ∞ a n 2 ∣ b n ∣ = 0 ∴ ∣ b n ∣ \\lim\\limits_n→∞\\dfraca_n^2b_n^2|b_n|=\\lim\\limits_n→∞a_n^2|b_n|=0 \\quad ∴|b_n| n→∞lim∣bn∣an2bn2=n→∞liman2∣bn∣=0∴∣bn∣更大。由比较审敛法,大的收敛,则小的 a n 2 b n 2 a_n^2b_n^2 an2bn2必收敛
答案:C
③比较审敛法极限形式
④比值法
⑤根值法
⑥极限审敛法
⑦积分判别法
⑧A-D判别法(任意项级数)
⑨绝对收敛必收敛 (任意项级数)
2.交错级数审敛法 —— 莱布尼茨收敛定理
莱布尼茨收敛定理:
若交错级数
∑
n
=
1
∞
(
−
1
)
n
−
1
u
n
\\sum_n=1^∞(-1)^n-1u_n
∑n=1∞(−1)n−1un 满足
u
n
u_n
un单调递减趋于0,则交错级数收敛
即满足 (1)
u
n
≥
u
n
+
1
u_n≥u_n+1
un≥un+1 (2)
lim
n
→
∞
u
n
=
0
\\lim\\limits_n→∞u_n=0
n→∞limun=0.
例题:11年2.
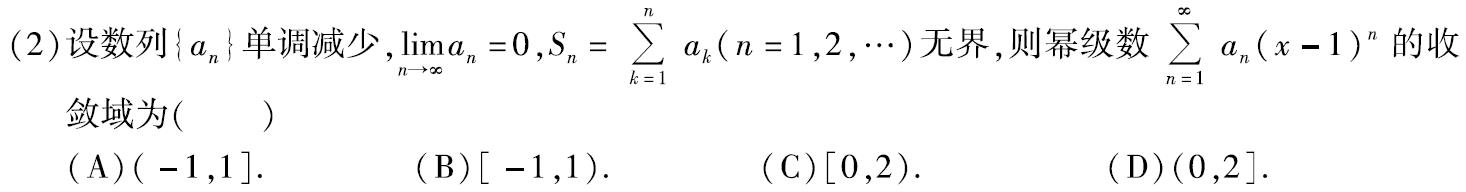
分析:显然
∑
n
=
1
∞
a
n
(
x
−
1
)
n
\\sum\\limits_n=1^∞a_n(x-1)^n
n=1∑∞an(x−1)n 的收敛中心为 x=1,故排除AB
代入x=2,得发散,所以2处应该为开区间,选C
答案:C
3.常用于举反例的一般项
a n = 1 n a_n=\\dfrac1n an=n1 或 a n = ( − 1 ) n ⋅ 1 n a_n=(-1)^n·\\dfrac1n an=(−1)n⋅n1
a n = ( − 1 ) n ⋅ 1 n a_n=(-1)^n·\\dfrac1\\sqrtn an=(−1)n⋅n1
(二) 幂级数
e x = ∑ k = 0 ∞ x k k ! e^x=\\sum\\limits_k=0^∞\\dfracx^kk! ex=k=0∑∞k!xk
∴ e = ∑ k = 0 ∞ 1 k ! = lim x → ∞ ( 1 + 1 x ) x ∴e=\\sum\\limits_k=0^∞\\dfrac1k!=\\lim\\limits_x→∞(1+\\dfrac1x)^x ∴e