用Python实现神经网络（附完整代码）！
Posted Datawhale
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了用Python实现神经网络（附完整代码）！相关的知识，希望对你有一定的参考价值。
↑↑↑关注后"星标"Datawhale
每日干货 & 每月组队学习，不错过
Datawhale干货
作者：[美]霍布森·莱恩，科尔·霍华德
在学习神经网络之前，我们需要对神经网络底层先做一个基本的了解。我们将在本节介绍感知机、反向传播算法以及多种梯度下降法以给大家一个全面的认识。
一、感知机
数字感知机的本质是从数据集中选取一个样本（example），并将其展示给算法，然后让算法判断“是”或“不是”。一般而言，把单个特征表示为xi，其中i是整数。所有特征的集合表示为 ，表示一个向量： ，
类似地，每个特征的权重表示为 其中 对应于与该权重关联的特征 的下标，所有权重可统一表示为 一个向量 :
这里有一个缺少的部分是是否激活神经元的阈值。一旦加权和超过某个阈值，感知机就输出1，否则输出0。我们可以使用一个简单的阶跃函数（在图5-2中标记为“激活函数”）来表示这个阈值。
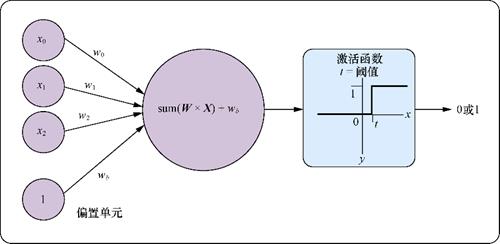
一般而言我们还需要给上面的阈值表达式添加一个偏置项以确保神经元对全0的输入具有弹性，否则网络在输入全为0的情况下输出仍然为0。
注：所有神经网络的基本单位都是神经元，基本感知机是广义神经元的一个特例，从现在开始，我们将感知机称为一个神经元。
二、反向传播算法
2.1 代价函数
很多数据值之间的关系不是线性的，也没有好的线性回归或线性方程能够描述这些关系。许多数据集不能用直线或平面来线性分割。比如下图中左图为线性可分的数据，而右图为线性不可分的数据：
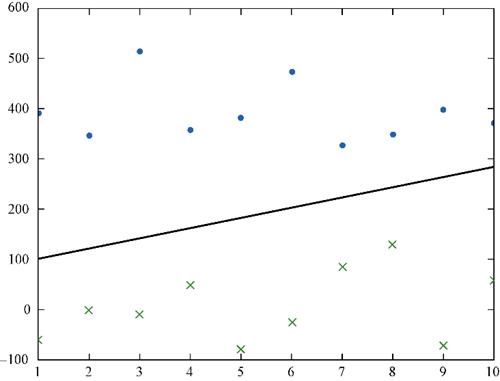
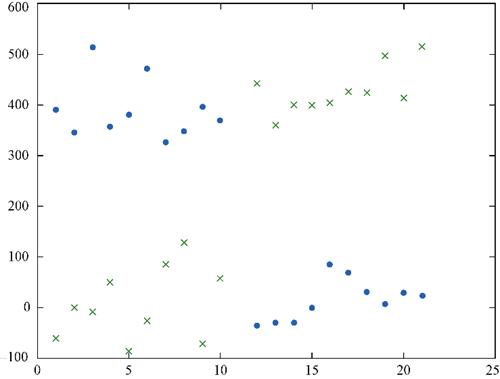
在这个线性可分数据集上对两类点做切分得到的误差可以收敛于0，而对于线性不可分的数据点集，我们无法做出一条直线使得两类点被完美分开，因此我们任意做一条分割线，可以认为在这里误差不为0，因此我们需要一个衡量误差的函数，通常称之为代价函数：
而我们训练神经网络（感知机）的目标是最小化所有输入样本数据的代价函数
2.2 反向传播
权重 通过下一层的权重（ ）和（ ）来影响误差，因此我们需要一种方法来计算对
神经网络进阶-用python实现一个完整的神经网络框架并在CIFAR10数据集上调参
Tensorflow实现LeNet5网络并保存pb模型，实现自定义的手写数字识别（附opencv-python调用代码）