龙格-库塔(Runge-Kutta)方法数学原理及实现

Posted 2022-09-16 SuPhoebe

龙格-库塔(Runge-Kutta)方法

龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法。由于此算法精度高，采取措施对误差进行抑制，所以其实现原理也较复杂。该算法是构建在数学支持的基础之上的。

---

对于一阶精度的欧拉公式有：

$$y_i+1 = y_i + hk_i$$
其中 $h$为步长，则$y_i+1$的表达式与 $y(x_i+1)$的Taylor展开式的前两项完全相同，即

局部截断误差

为 $O(h^2)$。
当用点 $x_i$处的斜率近似值 $k_1$与右端点 $x_i+1$处的斜率 $k_2$的算术平均值作为平均斜率 $k^*$的近似值，那么就会得到二阶精度的改进欧拉公式：
$$y_i+1 = y_i + h(k_1 + k_2)$$
其中 $k_1 = f(x_i,y_i)$ ， $k_2 = f(x_i + h,y_i + hk_1)$
依次类推，如果在区间 $[x_i, x_i+1]$内多预估几个店上的斜率值 $k_1,k_2,\\ldots,k_m$，并用他们的加权平均数作为平均斜率 $k^*$的近似值，显然能够构造出具有很高精度的高阶计数公式。
上述两组公式在形式删过的共同点：都是用 $f(x,y)$在某些点上值得线性组合得出 $y(x_i+1)$的近似值 $y_i+1$，且增加计算的次数，可以提高截断误差的阶，他们的误差估计可以用 $f(x,y)$在 $x_i$处的Taylor展开来估计。

---

于是可考虑用函数$f(x,y)$在若干点上的函数值的线性组合老构造金斯公式，构造时要求近似公式在$f(x_i,y_i)$处的Taylor展开式与解$y(x)$在$x_i$处的Taylor展开式的前面几项重合，从而使金斯公式达到所需要的阶数。既避免求高阶导数，又提高了计算方法精度的阶数。或者说，在$[x_i,x_i+1]$这一步内计算多个点的斜率值，若够将其进行加权平均作为平均斜率，则可构造出更高精度的计算格式，这就是龙格-库塔(Runge-Kutta)方法。
一般的龙格-库塔法的形式为

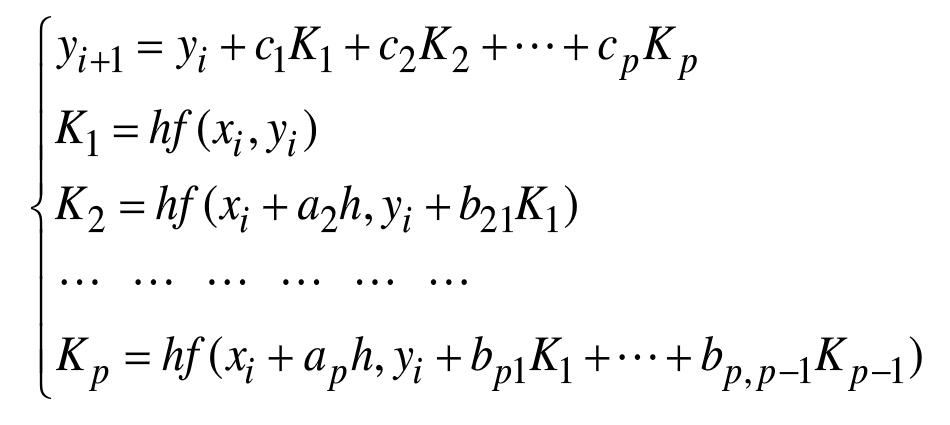
称为P阶龙格-库塔方法。
其中 $a_i,b_ij,c_j$为待定参数，要求上式 $y_i+1$在点 (xi,yi)龙格库塔（Runge-Kutta）法求四元数微分方程

四阶龙格库塔（Runge-Kutta）求解微分方程-多种编程语言

Runge-Kutta龙格-库塔法求解微分方程matlab仿真

基于龙格-库塔法Runge-Kutta的常微分方程的求解matlab仿真

四阶龙格库塔（Runge-Kutta）求解微分方程-多种编程语言

matlab代码实现四阶龙格库塔求解微分方程