神经网络学习 之 BP神经网络

Posted 2022-09-16 SuPhoebe

上一次我们讲了M-P模型，它实际上就是对单个神经元的一种建模，还不足以模拟人脑神经系统的功能。由这些人工神经元构建出来的网络，才能够具有学习、联想、记忆和模式识别的能力。BP网络就是一种简单的人工神经网络。
本文具体来介绍一下一种非常常见的神经网络模型——反向传播(Back Propagation)神经网络。

概述

BP（Back Propagation）神经网络是1986年由Rumelhart和McCelland为首的科研小组提出，参见他们发表在Nature上的论文 Learning representations by back-propagating errors 。

BP神经网络是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的 输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法，通过反向传播来不断 调整网络的权值和阈值，使网络的误差平方和最小。

BP算法的基本思想

上一次我们说到，多层感知器在如何获取隐层的权值的问题上遇到了瓶颈。既然我们无法直接得到隐层的权值，能否先通过输出层得到输出结果和期望输出的误差来间接调整隐层的权值呢？BP算法就是采用这样的思想设计出来的算法，它的基本思想是,学习过程由信号的正向传播与误差的反向传播两个过程组成。

• 正向传播时，输入样本从输入层传入,经各隐层逐层处理后,传向输出层。若输出层的实际输出与期望的输出(教师信号)不符,则转入误差的反向传播阶段。
• 反向传播时，将输出以某种形式通过隐层向输入层逐层反传,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号,此误差信号即作为修正各单元权值的依据。

这两个过程的具体流程会在后文介绍。

BP算法的信号流向图如下图所示

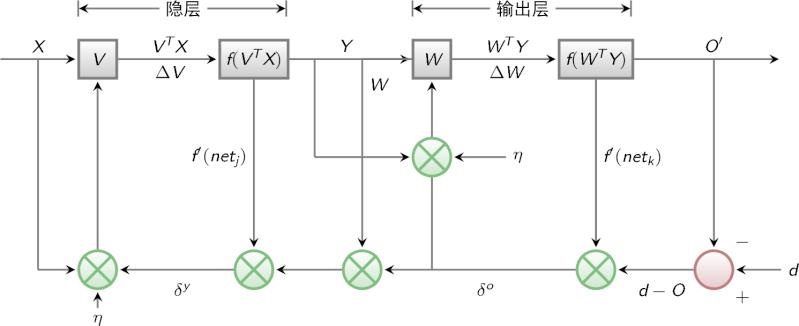
BP网络特性分析——BP三要素

我们分析一个ANN时，通常都是从它的三要素入手，即
1)网络拓扑结构；
2)传递函数；
3)学习算法。

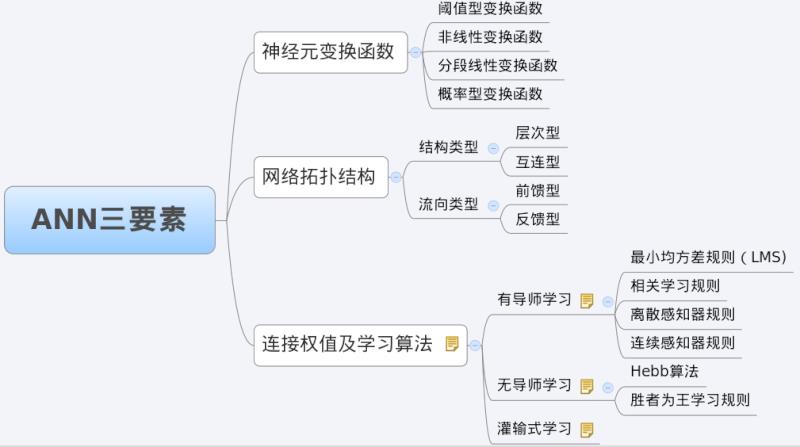
每一个要素的特性加起来就决定了这个ANN的功能特性。所以，我们也从这三要素入手对BP网络的研究。

3.1 BP网络的拓扑结构

上一次已经说了，BP网络实际上就是多层感知器，因此它的拓扑结构和多层感知器的拓扑结构相同。由于单隐层（三层）感知器已经能够解决简单的非线性问题，因此应用最为普遍。三层感知器的拓扑结构如下图所示。
一个最简单的三层BP：

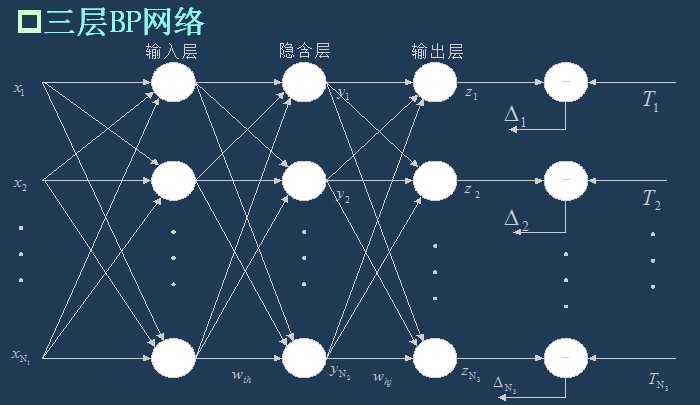
###3.2 BP网络的传递函数
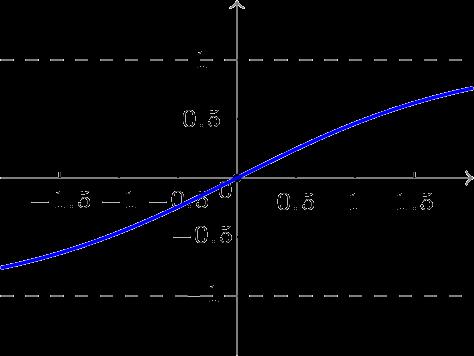
BP网络采用的传递函数是非线性变换函数——Sigmoid函数（又称S函数）。其特点是函数本身及其导数都是连续的，因而在处理上十分方便。为什么要选择这个函数，等下在介绍BP网络的学习算法的时候会进行进一步的介绍。
单极性S型函数曲线如下图所示。
$$f(x)=\frac{1}{1+e^{-x}}$$

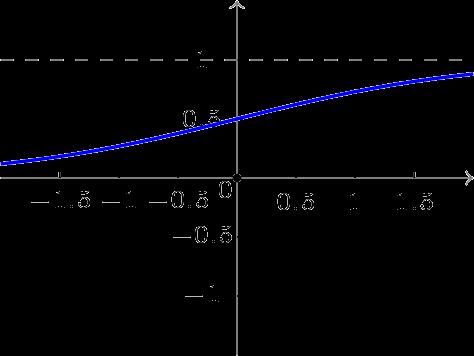
双极性S型函数曲线如下图所示。
$$f(x)=\frac{1-e^{-x}}{1+e^{-x}}$$

3.3 BP网络的学习算法

BP网络的学习算法就是BP算法，又叫 δ 算法（在ANN的学习过程中我们会发现不少具有多个名称的术语）， 以三层感知器为例，当网络输出与期望输出不等时，存在输出误差 E ，定义如下

$$E=\frac{1}{2}(d-O{)}^2=\frac{1}{2}\sum _{\kappa =1}^{\ell }(d_k-o_k{)}^2$$

将以上误差定义式展开至隐层，有
$$E=\frac{1}{2}\sum _{\kappa =1}^{\ell }[d_{\kappa }-f(ne{t}_{\kappa }){]}^2=\frac{1}{2}\sum _{\kappa =1}^{\ell }[d_{\kappa }-f(\sum _{j=0}^m{\omega }_{j\kappa }{y}_j){]}^2$$

进一步展开至输入层，有
$$E=\frac{1}{2}\sum _{\kappa =1}^{\ell }{d_{\kappa }-f[\sum _{j=0}^m{\omega }_{j\kappa }f(ne{t}_j)]}^2=\frac{1}{2}\sum _{\kappa =1}^{\ell }{d_{\kappa }-f[\sum _{j=0}^m{\omega }_{j\kappa }f(\sum _{j=0}^n{\upsilon }_{ij}{\chi }_i)]}^2$$

由上式可以看出，网络输入误差是各层权值${\omega }_{j\kappa }$、${\upsilon }_{ij}$的函数，因此调整权值可改变误差 $E$。 显然，调整权值的原则是使误差不断减小，因此应使权值与误差的梯度下降成正比，即
$$\Delta {\omega }_{j\kappa }=-\eta \frac{\partial E}{\partial {\omega }_{j\kappa }}j=0,1,2,\dots ,m;\kappa =1,2,\dots ,\ell$$

$$\Delta {\upsilon }_{ij}=-\eta \frac{\partial E\partial }{{\upsilon }_{ij}}i=0,1,2,\dots ,n;j=1,2,\dots ,m$$

对于一般多层感知器，设共有 $h$ 个隐层，按前向顺序各隐层节点数分别记为 m 1 , m 2 , … , m h m_1,m_2,…,m_h 智能计算之神经网络(BP)介绍

基于BP神经网络的草莓等级识别，BP神经网络的详细原理，神经网络1000案例之7

图像识别基于BP神经网络实现手写字母识别matlab源码

常见神经网络类型之前馈型神经网络

深度学习——MP神经元模型, BP算法, 神经元激活函数, Dropout

机器学习从入门到精通系列之BP神经网络理论知识详解