二叉树系列——二叉树的最大距离（即相距最远的两个叶子节点，编程之美，百度面试题）

Posted 2022-09-16 liuyi1207164339

来自于编程之美3.8。

参考：http://www.cnblogs.com/miloyip/archive/2010/02/25/1673114.html 这里有比较详细的讨论！

题目：如果我们把二叉树看做图，父子节点之间的连线看成是双向的，我们姑且定义“距离”为两个节点之间边的个数。写一个程序求一棵二叉树中相距最远的两个节点之间的距离。

如下图所示，树中相距最远的两个节点为A,B，最大距离为6。

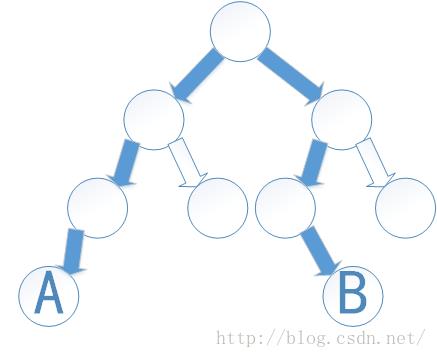
书上对这个问题的分析是很清楚的，计算一个二叉树的最大距离有两个情况：

情况A: 路径经过左子树的最深节点，通过根节点，再到右子树的最深节点。
情况B: 路径不穿过根节点，而是左子树或右子树的最大距离路径，取其大者

对于情况A来说，只需要知道左右子树的深度，然后加起来即可。

对于情况B来说，需要知道左子树的最远距离，右子树的最远距离。

只需要计算这两种情况的路径距离，并取其最大值，就是该二叉树的最大距离。

           

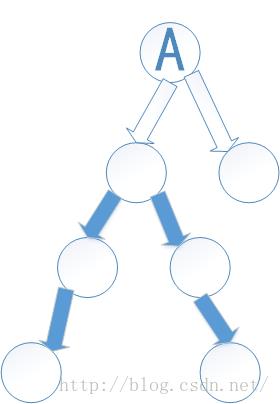
             情况A                                                        情况B

下面是书上的源码：

struct NODE

	NODE* pLeft;        // 左子树
	NODE* pRight;       // 右子树
	int nMaxLeft;       // 左子树中的最长距离
	int nMaxRight;      // 右子树中的最长距离
	char chValue;       // 该节点的值
;

int nMaxLen = 0;

// 寻找树中最长的两段距离
void FindMaxLen(NODE* pRoot)

	// 遍历到叶子节点，返回
	if (pRoot == NULL)
	
		return;
	

	// 如果左子树为空，那么该节点的左边最长距离为0
	if (pRoot->pLeft == NULL)
	
		pRoot->nMaxLeft = 0;
	

	// 如果右子树为空，那么该节点的右边最长距离为0
	if (pRoot->pRight == NULL)
	
		pRoot->nMaxRight = 0;
	

	// 如果左子树不为空，递归寻找左子树最长距离
	if (pRoot->pLeft != NULL)
	
		FindMaxLen(pRoot->pLeft);
	

	// 如果右子树不为空，递归寻找右子树最长距离
	if (pRoot->pRight != NULL)
	
		FindMaxLen(pRoot->pRight);
	

	// 计算左子树最长节点距离
	if (pRoot->pLeft != NULL)
	
		pRoot->nMaxLeft = ((pRoot->pLeft->nMaxLeft > pRoot->pLeft->nMaxRight) ? pRoot->pLeft->nMaxLeft : pRoot->pLeft->nMaxRight) + 1;
	

	// 计算右子树最长节点距离
	if (pRoot->pRight != NULL)
	
		pRoot->nMaxRight = ((pRoot->pRight->nMaxLeft > pRoot->pRight->nMaxRight) ? pRoot->pRight->nMaxLeft : pRoot->pRight->nMaxRight)+1;
	

	// 更新最长距离
	if (pRoot->nMaxLeft + pRoot->nMaxRight > nMaxLen)
	
		nMaxLen = pRoot->nMaxLeft + pRoot->nMaxRight;
	

以上代码得新定义一个Node类型，且代码比较复杂！

下面是精简版：

首先我们知道求二叉树的深度的代码是比较简单的，代码如下：

int DepthOfBinaryTree(BinaryTreeNode*pNode)
	if (pNode==NULL)
	
		return 0;
	
	else  //递归
		return DepthOfBinaryTree(pNode->m_pLeft) > DepthOfBinaryTree(pNode->m_pRight) ?
			   DepthOfBinaryTree(pNode->m_pLeft) + 1 : DepthOfBinaryTree(pNode->m_pRight) + 1;
	

而我们要求的二叉树的最大距离其实就是求：肯定是某个节点左子树的高度加上右子树的高度加2，所以求出每个节点左子树和右子树的高度，取左右子树高度之和加2的最大值即可，假设空节点的高度为-1

代码如下：

//改进的版本
int HeightOfBinaryTree(BinaryTreeNode*pNode, int&nMaxDistance)
	if (pNode == NULL)
		return -1;   //空节点的高度为-1
	//递归
	int nHeightOfLeftTree = HeightOfBinaryTree(pNode->m_pLeft, nMaxDistance) + 1;   //左子树的的高度加1
	int nHeightOfRightTree = HeightOfBinaryTree(pNode->m_pRight, nMaxDistance) + 1;   //右子树的高度加1
	int nDistance = nHeightOfLeftTree + nHeightOfRightTree;    //距离等于左子树的高度加上右子树的高度+2
	nMaxDistance = nMaxDistance > nDistance ? nMaxDistance : nDistance;            //得到距离的最大值
	return nHeightOfLeftTree > nHeightOfRightTree ? nHeightOfLeftTree : nHeightOfRightTree;

上面的函数的参数nMaxDistance返回的就是最大的距离，以下图作为测试。

                                                               

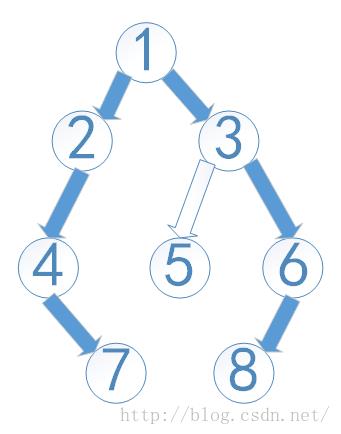
输出如下：

注意：在数据结构与算法分析这本书上面，树的深度是不包括根节点的，树的深度就等于树的高度，所以上面的函数的返回值是能够代表树的深度，也就是高度的！所以在判断pNode==NULL的时候返回-1。

但是在剑指offer：面试题39，树的深度包括了根节点，所以在判断pNode==NULL的时候返回0。

如上图所示：按剑指offer上面的，深度为4，但是按数据结构与算法分析，深度则为3！这个需要特别注意。