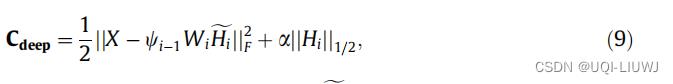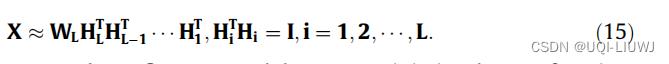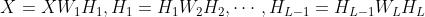论文笔记：A survey of deep nonnegative matrix factorization

Posted 2022-09-09 UQI-LIUWJ

0 abstract

• 深度非负矩阵分解（Deep NMF）是近年来一种有效的特征提取策略。
• 通过基于 NMF 算法反复分解矩阵，我们获得了分层神经网络结构，并探索了数据的更多可解释表示。
• 本文主要针对 Deep NMF 进行了一些理论研究，系统地介绍了其基本模型、优化方法、性质及其扩展和推广。
• 我们将 Deep NMF 算法分为五类：Deep NMF、Constrained Deep NMF、Generalized Deep NMF、Multi-View Deep Matrix Factorization (MF)、深度神经网络 (DNN) 与 NMF 之间的关联。
• 此外，我们研究了深度 NMF 算法在一些人脸数据库上的聚类性能。然后对Deep NMF方法的设计原则、主要步骤、关系、应用领域和演进进行了全面分析。
• 此外，还讨论了 Deep NMF 的一些开放问题。

1 introduction

• 现在各个领域中，数据量很丰富的
  • 现在有很多方法来降低数据量的丰富程度（PCA、LPP、LDA等）
  • 但是，有很多真实数据都需要满足非负性，而上述方法有没有非负条件的约束
    • ——>非负矩阵分解(NMF)被提了出来
    • ——>NMF将非负矩阵V分解成非负的低秩矩阵W和H（分别叫做基础矩阵basis matrix和特征矩阵feature matrix）
    • ——>目标是希望V和WH之间的欧几里得距离、KL散度值越小越好
  • 尽管NMF在很多领域有很好的泛化能力&物理含义，但是它只考虑了数据的浅层信息
  • 单层结构并不能获得很多不同角度的表征
    • ——>最近很多模型把单层NMF推广到了多层结构中（Multiple NMF）
  • 随着深度学习的热门，最近也有研究者将NMF与深度学习框架相结合（Deep NMF）
• 深度NMF模型可以被划分成五个类别：
  • 深度NMF——只包含了非负这一个约束
  • 加约束的深度NMF——深度NMF的基础上，加了一些额外的约束来作为正则项
  • 广义深度NMF——延申了传统的分解模型
  • 多视角深度MF——在多视角（multi-view）的数据中使用深度矩阵分解
  • 可以体现DNN&NMF之间关系的模型

2 深度NMF

2.1 DNMF介绍

• 基础的NMF可以被视为一个单层的学习过程，同时从数据矩阵X种学习基础矩阵W和特征矩阵H
• 为了使用多层NMF来发掘数据中的层级特征，我们分解从单层NMF中学到的特征矩阵H1，至W2,H2
  • ——>这样的话，我们就把单层NMF拓展到了双层NMF结构
• 相似的方式，我们把数据矩阵X分解成L+1层特征
  • 
  • 其中
  • 这样每一层的非负隐式特征可以表示为
    • 
    • 
    • ......
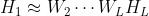
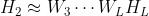
  • ——>有很好的解释性（高层特征包含着底层特征）
• 深度NMF算法一般是由两步组成的
  • 预训练阶段
    • 这一阶段对每一层使用单层的非负矩阵分解算法
    • 矩阵X—>W1和H1
    • 矩阵H1—>W2和H2
    • .....直到L层
  • 精调阶段
    • 当所有单层NMF都OK了之后进行的
    • 精调所有的矩阵，根据如下的目标函数

Deep transductive nonnegative matrix factorization for  speech separation	提出了一种基于上述 Deep NMF 基本框架的深度转导 NMF 模型（DTNMF） 学习了一个关于每个说话者的源信号的共享字典，用于分离单通道语音信号的混合。
Deep non-negative matrix factorization architecture  based on underlying basis images learning,  A deep orthogonal non-negative matrix factorization method for learning attribute representations,	不分解特征矩阵H，分解基础矩阵W

2.2 DNMF的优化方式【经典方式】

2.2.1 第一阶段

第一阶段（单层NMF）：交替最小二乘法（ANLS)

2.2.2 第二阶段

 第二阶段（精调）：近似更新准则

将损失函数重写成： 

其中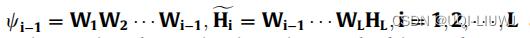

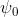是单位矩阵

通过选择梯度的非负方向来更新 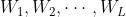和

计算梯度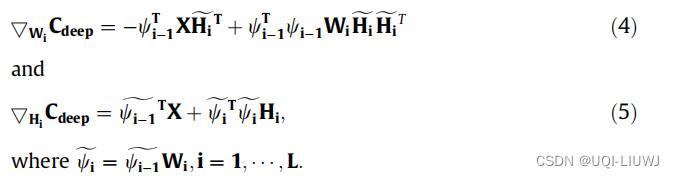

采用适当的步长，微调阶段第 i 层的更新规则为（虽然我不清楚这是怎么推出来的。。。）

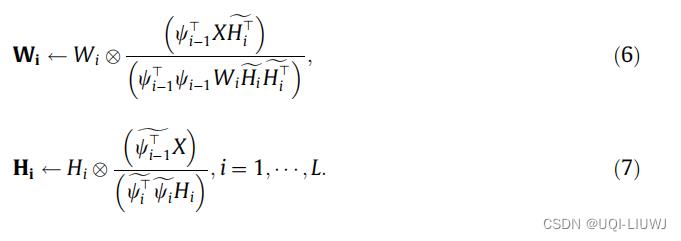
2.2.3 优缺点 

优点：计算复杂度低

缺点：收敛速度慢、会调入局部最优点

 

3 Constrained deep NMF algorithms

在W和H上加入约束条件

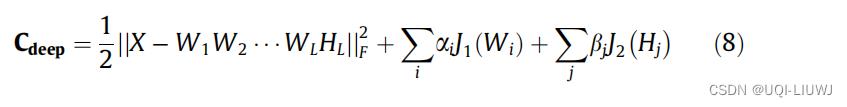
 3.1 稀疏deep NMF

稀疏约束广泛用于单层约束 NMF 问题。 这种限制条件有助于提高分解的唯一性。

l1范数+NMF	Non-negative sparse coding
l2范数+NMF	Improving molecular cancer class discovery through sparse non-negative matrix factorization
	Regression shrinkage and selection via the lasso: a retrospective 证明二次项可能导致矩阵的值减小但不稀疏。 换句话说，基于 l1-norm 的稀疏约束模型比基于 l2-norm 的模型更有效。
l1范数+DNMF	Sparsity-constrained deep nonnegative matrix factorization for hyperspectral unmixing 对每个特征矩阵Hi进行L1番薯约束
l1/2范数+DNMF	l1-norm 的一个缺点是它不满足完全可加性 Hyperspectral unmixing using sparsity-constrained deep nonnegative matrix factorization with total variation
	Spectral unmixing of hyperspectral imagery using multilayer nmf

 3.2 正交deep NMF

On the equivalence of nonnegative matrix factorization and spectral clustering The relationships among various nonnegative matrix factorization methods for clustering

• 正交的一个好处是可以解释成聚类clustering
  • 如果正交作用在W矩阵的列上()
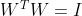    • ——>数据矩阵X的每一列可以被用来聚类
  • 如果H的行是正交的（）
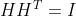    • ——>数据矩阵的每一行可以用来聚类

对W和H同时进行正交处理	Orthogonal nonnegative matrix tri-factorizations for clustering 提出了ONMF
近似正交 NMF	有的时候一个样本不一定只属于一个cluster，严格正交是不对的  Two effificient algorithms for approximately orthogonal nonnegative matrix factorization, 提出了ANOMF
DONMF	A deep orthogonal non-negative matrix factorization  method for learning attribute representations DONMF 的目的是进一步分解 W，为 ONMF 或 AONMF 配备深度架构，使 ONMF 能够： （1）自动学习潜在的属性层次结构； (2) 基于高级抽象，找到更适合聚类分析的数据表示。

3.3 判别式DNMF

NMF算法是一种无监督学习方法。 因此，可以在分类设置中将判别信息添加到 NMF 方法中

Fisher 判别限制+NMF	Weighted fifisher non-negative matrix factorization for face  recognition Fisher non-negative matrix factorization for learning local features 正则项是由类内分布和类间分布表示
自监督NMF	Facial expression recognition based on  graph-preserving sparse non-negative matrix factorization, 约束非负矩阵分解（CNMF），获取部分数据标签信息并将其作为附加约束。 这种方法可以保证相同标签的数据映射到子空间中的同一个类。

3.4 利用空间信息的DNMF

局部不变性 ：从高维空间映射到低维空间后可以保留几何特征信息

NMF+图拉普拉斯	Graph laplacians and their convergence  on random neighborhood graphs Weighted graph laplacians and isoperimetric inequalities
Graph regularized Multi-layer Concept Factorization (GMCF)	Graph regularized multilayer concept factorization for data representation, 使用Concept Factorization
GCMF+L 1/2范数	Deep convex nmf for image clustering
双正交约束的半监督图正则化深度 NMF（SGDNMF）	GMCF只计算两个顶点之间的距离，不能充分利用数据点之间的高阶关系。 GMCF 只保留数据的局部结构，同时忽略特征的几何形状。 为了解决这些问题，Semi-supervised graph  regularized deep nmf with bi-orthogonal constraints for data representation, 提出了一种新的半监督深度学习算法SGDNMF。 SGDNMF它在每一层都应用了双超图拉普拉斯正则化，而不是以前文献中使用的常见图拉普拉斯。  目标函数是

4 广义DNMF

 4.1 深度半非负矩阵分解

• semi-NMF中，原始矩阵X和基础矩阵W是无限制的，只有特征矩阵H需要被限制为非负的
• Semi-nonnegative matrix factorization for motion  segmentation with missing data

• 深度semi-NMF  A deep matrix factorization method for learning attribute representations
  • 这里g是一个非线性函数

4.2 深度非光滑NMF

• 3.1 节介绍的稀疏 NMF 算法试图通过在基本 NMF 目标函数中附加惩罚项来获得稀疏分解矩阵。
• 这种约束可以应用于基矩阵 W 或特征矩阵 H。
• 但是，当对一个矩阵施加稀疏约束时，另一个矩阵几乎是非稀疏的。

• 因此，Nonsmooth nonnegative matrix factorization (nsnmf) 提出了非平滑 NMF (nsNMF)，通过插入平滑矩阵 S 来改变 NMF 模型，使得 X=WSH。 该模型产生更稀疏的编码向量并增强了可解释性         

Learning the hierarchical parts of objects by  deep non-smooth nonnegative matrix factorization

提出了deep non-smooth NMF（dns NMF）