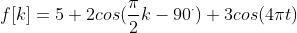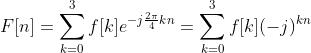数学笔记;离散傅里叶变化 DFT
Posted UQI-LIUWJ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数学笔记;离散傅里叶变化 DFT相关的知识,希望对你有一定的参考价值。
1 原理介绍
- 离散傅里叶变化是连续傅里叶变化在如下信号下的等价形式:
- N个样本
- 每个样本的采样间隔是T
- 令f(t)是数据源的持续信号,将N个样本表示成f[0],f[1],f[2],.....f[k],....f[N-1]
- ——>原始数据源信号f(t)的傅里叶变换,应该是
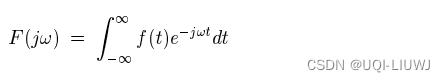
- ——>原始数据源信号f(t)的傅里叶变换,应该是
- 因为信号脉冲仅在样本点采集,所以可以如下近似:
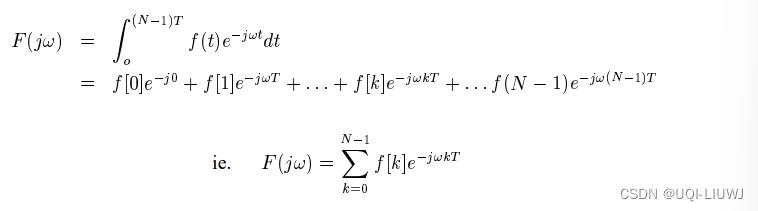
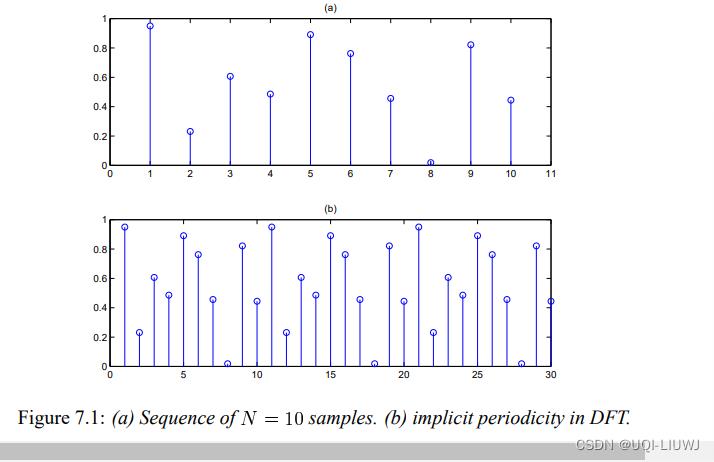
- 这里,DFT假设波形是周期性的(周期正好是T个interval的跨度)
- 也就是这里我们是从0到N-1采样的f(0)到f(N-1),和从N到2N-1采样得到的f(N)到f(2N-1)是一样的
- 比如我们采样了10个点(0~10),那么DFT会隐式地人为周期就是10
-
所以上式中的ω被表示为:
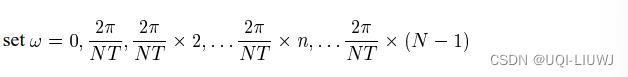
-
所以离散傅里叶级数可以表示为:
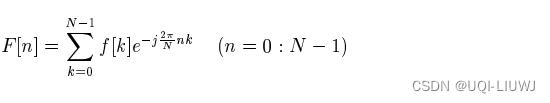
-
上式可以被重写成:
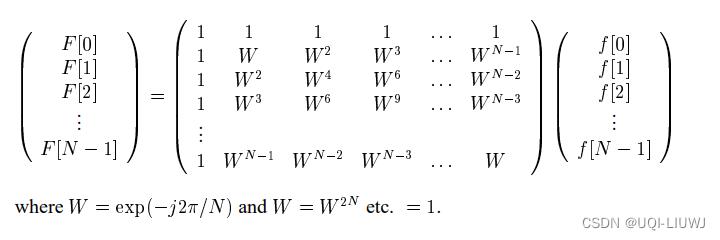
1.1 欧拉公式 (复习)

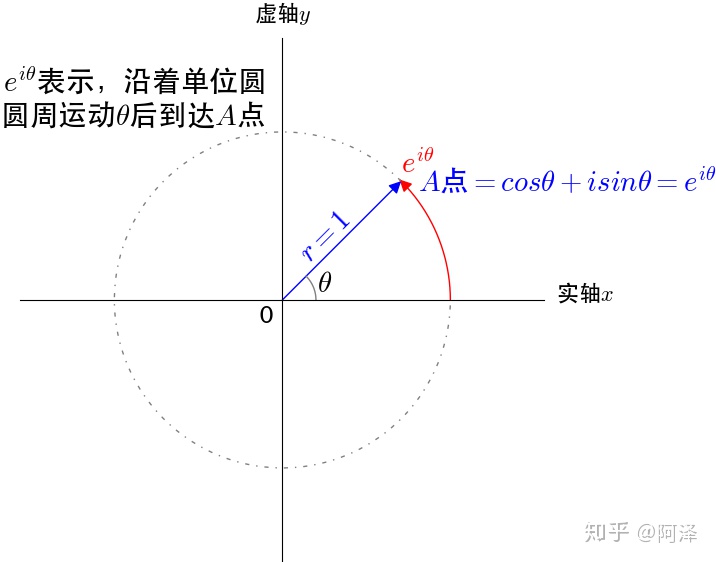
2 举例
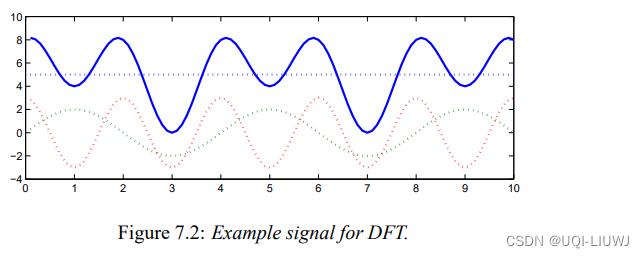
令连续信号为:
采样k=0~k=3 四个点,得到f[0]=8,f[1]=4,f[2]=8,f[3]=0
于是
可以写成:
用矩阵的形式,可以写成
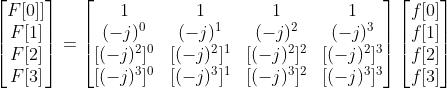
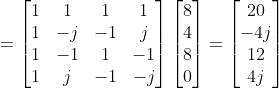
4 逆傅里叶变化
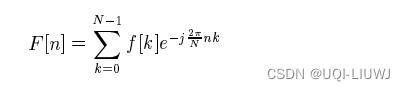
的逆傅里叶变化是:
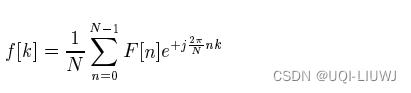
如果这里令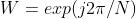 的话,那么逆傅里叶变化的矩阵形式为
的话,那么逆傅里叶变化的矩阵形式为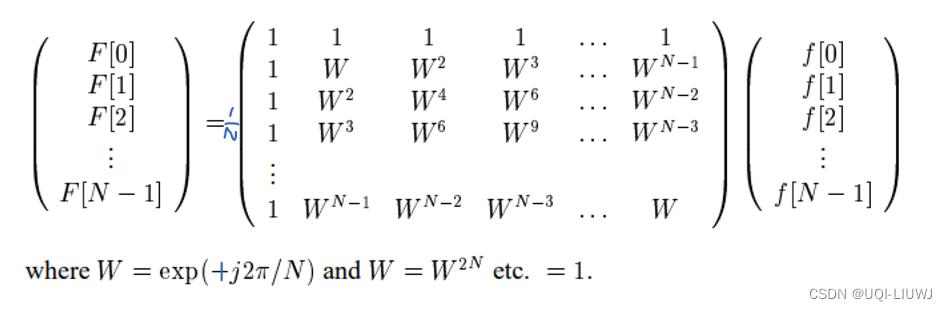
4.1 举例
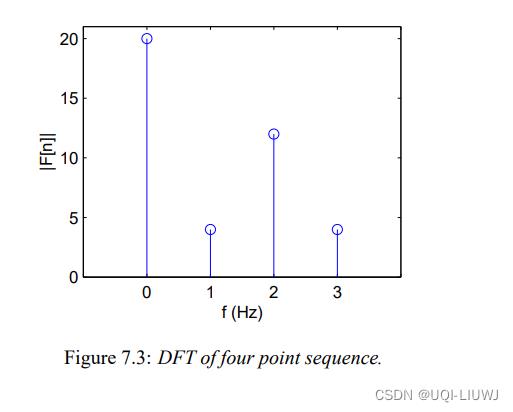
还是用前面一个例子
已知F[0]=20,F[1]=-4j,F[2]=12,F[3]=4j
希望得到:f[0]=8,f[1]=4,f[2]=8,f[3]=0
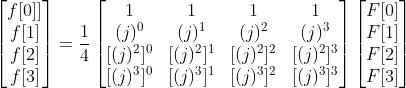
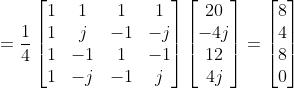
以上是关于数学笔记;离散傅里叶变化 DFT的主要内容,如果未能解决你的问题,请参考以下文章