《程序员的数学：8 不可解的问题》

Posted 2022-09-02 bohu83

本文属于《程序员的数学》读书笔记系列。本篇真没看明白。太抽象了，我觉得超越我自己的语言表达范围了，尽量贴一下书上的原文。

反证法

 先假设命题的否定形式成立，再进行推理，引出矛盾。

可数

  无穷可以分为可数无穷和不可数无穷。
所谓可数无穷是指可以按照一定的规律或者表达方式来表达（即无遗漏，也无重复）。这种情况下在集合的定义中表达为“与正整数意义对应”。

例如：

-有限集合是可数的
-0以上的所有偶数的集合是可数的
-0以上的所有奇数的集合是可数的
-所有整数的集合是可数的
-所有有理数的集合是可数的

  啥是有理数，都忘了。有理数为整数（正整数、0、负整数）和分数的统称。

程序的集合是可数的。（因为编写程序的字符种类有限，假设有N个字符，那么）

所以有不可数的集合吗？

不可数的集合确认存在。

对角论证法

假设我们要证明所有整数数列的集合是不可数的，那么反证就是假设所有整数数列的集合是可数的，此处是运用的反证法。

既然所有整数数列是可数的，那无论哪个整数数列都可以编号，现在我们按下图的方式来列出所有整数数列，编号为k的整数列在表的k行。

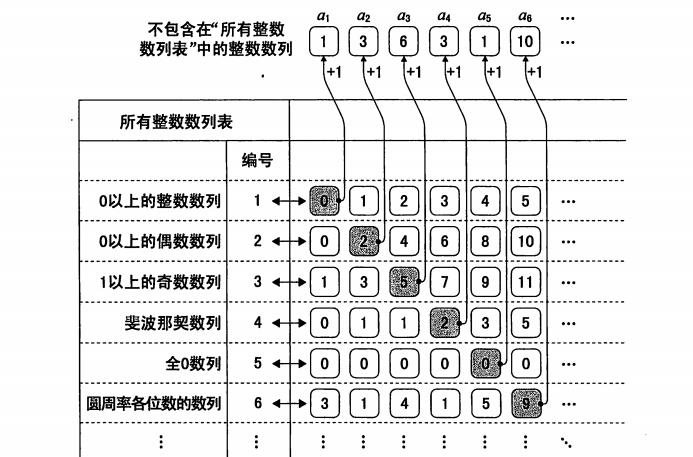
目标是找出不包含在 “所有整数数列”的整数数列，得出矛盾的结果。

    如果按照图中第k行的第k个元素ak单独组出一组数列a1,a2,a3......ak的话，从第1列的第1个数+1 记为a1，到第K列的第k个数+1 记为ak. a1,a2,a3....ak是整数数列，但是不包含在“所有的整数数列列表”，为什么呢？ 因为它与所有整数数列中任意数列，至少有一处不同。

    “所有的整数数列列表” 应该包含所有整数数列，但是却没有包含a1,a2,a3.。。。。这是矛盾的。说明命题错误，命题所有整数数列的集合是不可数的为真。

除此之外
-所有实数的集合是不可数的
-所有函数的集合也是不可数的。

感兴趣的看书吧。

 不可解问题

 不可解的问题并非是“花大量时间求解问题”，而是“原则上不能用程序来解决的问题”。

   事实上，不能写成程序的函数是存在的。

停机问题

 这是图灵提出来的，当然受到哥德尔不完全性定理的影响。哥德尔证明了任何一个形式系统，只要包括了简单的初等数论描述，而且是自洽的，它必定包含某些系统内所允许的方法既不能证明真也不能证伪的命题。图灵吧这个问题延伸到计算机领域。

   通俗地说，停机问题就是判断任意一个程序是否能在有限的时间之内结束运行的问题。该问题等价于如下的判定问题：是否存在一个程序P，对于任意输入的程序w，能够判断w会在有限时间内结束或者死循环。（有限时间并不指时间长短，而是指无论耗时多长，只要能有终止的一刻就好。）

  停机问题就是判断任意一个程序是否会在有限的时间之内结束运行的问题。如果这个问题可以在有限的时间之内解决，则有一个程序判断其本身是否会停机并做出相反的行为，这时候显然不管停机问题的结果是什么都不会符合要求。所以这是一个不可解的问题。

  下面证明解决停机问题的程序不存在。还是用反证法

1 假设可以写出判断程序haltchecker

将程序p和数据d 输入程序时记作 haltchecker（p,d）

haltchecker（p,d）=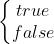   

true 表示p会在有限时间结束，false 表示 p不会再有限时间内结束。

2 写出slefloop程序

 selfloop(p)

    halts = haltchecker（p,p）;

    if(halts )

        while(1>0)

         

   

使用haltchecker，判断“对于程序p,将程序p本身作为输入会不会结束运行”

如果判断结果会，那么selfloop本身会无限循环。

如果判断不会，那么selfloop 会马上结束运行。

3. 推导出矛盾

把selfloop自身传入selfloop。判断运行情况。为了防止描述不清楚，贴一段原文。

这就说假设“能写出停机判断程序haltchecker”,必然产生矛盾。反证停机问题是不可见的。图灵在1936年证明了。

作者还一次为例，介绍了费马大定理，“当整数  时，关于  方程  没有正整数解。”等等，作为非数学专业，早已看不懂，但源于数学的悖论的除了刚才的图灵停机问题，现在有科学家尝试用不可解的理论去解决重大物理理论问题“杨-米尔斯存在性与质量间隙”。

   类似的还有理发师问题：村子里有个理发师，这个理发师有条原则是，对于村里所有人，当且仅当这个人不自己理发，理发师就给这个人理发。如果这个人自己理发，理发师就不给这个人理发。无法回答的问题是，理发师给自己理发么？

真的，人类知识复杂又爆炸，一个费马大定理前后证明用了几百年，现在还有那么多的知识是未知的。真心佩服那些大神，写出那么复杂的知识。我觉得超出我的认知范围，难以用语言表达。学数学真需要天赋。