2022 RoboCom 世界机器人开发者大赛-本科组（国赛）
Posted 小哈里
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了2022 RoboCom 世界机器人开发者大赛-本科组（国赛）相关的知识，希望对你有一定的参考价值。
文章目录
1、智能红绿灯
为了最大化通行效率同时照顾老年人穿行马路，在某养老社区前，某科技公司设置了一个智能红绿灯。
这个红绿灯是这样设计的：
路的两旁设置了一个按钮，老年人希望通行马路时会按下按钮；
在没有人按按钮的时候，红绿灯一直为绿灯；
当红绿灯为绿灯时，有人按下按钮，第一次按下按钮的 15 秒后绿灯会转红；
转红后，红灯会持续 30 秒，方便老年人穿行马路；
在 30 秒的红灯期间，假如有人再次按下按钮，则红灯会再延续 15 秒；
延续一次后不会再次延续。
现在给定按钮被按下的时间点，请你输出这个智能红绿灯的红灯时间区间。
注意：我们假设同一秒内，红绿灯先变化，然后按钮再被按下。每 1 秒理解为一个时间点。例如：在第 1 秒按下按钮，则第 16 秒开始变红；如果没有人在第 16 - 45 秒这个闭区间内按下按钮，则到第 46 秒开始变绿。而在第 46 秒按下按钮的人，需要等 15 秒后才有红灯。
输入格式:
输入第一行为 N (1≤N≤1000)，表示按钮被按下的次数。
接下来一行 N 个非负整数，表示按钮被按下的时间点。一个时间点按钮有可能会被多次按下，给出的时间点保证是不递减的。
时间点的范围不超过 10
4
。
输出格式:
输出若干行，按起始时间从小到大输出互不相交的红灯的时间区间。
输入样例:
10
3 4 5 6 33 45 49 70 90 100
输出样例:
18 62
85 129
代码长度限制
16 KB
时间限制
400 ms
内存限制
64 MB
题意：
- 模拟题
思路：
- 枚举每次按下按钮的时间， 维护区间数组表示红灯对应的时间段，根据题目规则修改即可。
//T1, AC
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1010;
int a[maxn];
int main()
int n; cin>>n;
for(int i = 1; i <= n; i++)
cin>>a[i];
vector<pair<int,int> >vc;
int l = a[1]+15, r = a[1]+15+30-1, ok = 0;
for(int i = 2; i <= n; i++)
if(a[i]<=r && a[i]>=l)
if(ok==0)
r += 15;
ok = 1;
else
if(a[i]>r)
ok = 0;
if(vc.empty() || vc.back()!=make_pair(l,r))vc.push_back(make_pair(l,r));
l = a[i]+15;
r = a[i]+15+30-1;
vc.push_back(make_pair(l,r));
for(auto x:vc)
cout<<x.first<<" "<<x.second<<"\\n";
return 0;
2、女王的大敕令
副本是游戏里的一个特色玩法，主要为玩家带来装备、道具、游戏资源的产出，满足玩家的游戏进程。
在 MMORPG《最终幻想14》里，有一个攻略人数最大达到 48 人的副本“零式贡希尔德神庙”，其中守关 BOSS “天佑女王”有一个很有趣的技能：“女王的大敕令”。
技能在一个 5×5 的棋盘上展开。每位玩家根据给定的两个步长，从某个方格出发，在棋盘上先走 D
1
步，再走 D
2
步。其中“步长”指的是曼哈顿距离，即：设两个方格的坐标分别为 (X
i
,Y
i
) 以及 (X
j
,Y
j
)，则这两个方格的曼哈顿距离 D=∣X
i
−X
j
∣+∣Y
i
−Y
j
∣。
例如下图中的 A 点与 B 点的曼哈顿距离为 5：
image.png
技能开始时，场地外围会出现 4 只小怪，东南西北（即棋盘的右、下、左、上）方向各出现一只小怪，且小怪一定出现在某行或某列对应的位置上。第 i 只小怪会顺时针朝固定方向移动 n
i
步（题目保证不会移出界，即移动后仍然在对应着某行/某列的位置上），且：
北边的小怪固定向右移动；
东边的小怪固定向下移动；
南边的小怪固定向左移动；
西边的小怪固定向上移动。
小怪出现后，棋盘上还会出现一个发光的格子，这是玩家移动的目标点，如图所示：
image.png
玩家必须在不被小怪杀死的前提下，按规定步长，用两个回合到达目标点。技能流程如下：
1、玩家先选择一个起始方格；
2、东、西两侧的小怪开始按照固定方向移动，移动完毕后 4 只小怪会同时开展攻击，其中东、西两侧的小怪攻击自己所对应的一整行，南、北两侧的小怪攻击自己所对应的一整列。玩家若处在攻击区内则任务失败。
3、玩家移动 D
1
步，到达某个方格；
4、南、北两侧的小怪开始按照固定方向移动，移动完毕后 4 只小怪会同时开展攻击，同第 2 步；
5、玩家移动 D
2
步，此时必须到达目标点，否则任务失败。
以下是上面的 4 只小怪都移动后的攻击范围的示意图：
image.png
给定小怪起始位置以及移动步数 n
i
和目标点位置，请输出所有安全的移动方案，包括起始点以及第一次移动的目的地。
输入格式:
输入第一行是四个数 C
1
,C
2
,R
1
,R
2
，分别表示：
北边（上面）的小怪 1 在第 C
1
列的位置上；
南边（下面）的小怪 2 在第 C
2
列的位置上；
西边（左边）的小怪 3 在第 R
1
行的位置上；
东边（右边）的小怪 4 在第 R
2
行的位置上。
输入第二行是四个数 n
i
（i=1,⋯,4），按照上面的顺序给出小怪移动的步数，保证小怪移动后仍然处于某行或某列对应的位置上。
输入第三行是四个数 row,col,D
1
,D
2
，依次表示目标点的位置，以及玩家要走的两个步长。这里某方格的“位置” (row,col) 指的是该方格的行号、列号组成的二元组。
我们假设左上角的方格位置为 (1, 1)。
输出格式:
输出安全移动的方案，方案由两个位置共四个数组成，前两个数为初始选择的方格的位置，后两个数为第一次停留的位置。
对于多个方案的情况，先按初始方格位置从小到大输出，初始方格相同时按第一次停留位置从小到大输出。一个坐标 (r
i
,c
i
) 比另一个坐标 (r
j
,c
j
) 小，当且仅当 r
i
<r
j
，或 r
i
=r
j
的同时有 c
i
<c
j
。
输入样例:
2 4 4 2
1 2 3 2
5 3 3 4
输出样例:
2 1 2 4
2 3 3 1
2 3 3 5
题意：
- 模拟题
思路：
- 地图大小只有5*5，因此可以直接四层循环暴力枚举起点的位置和第一次转弯的位置，然后判断一下是否会被攻击到即可。
//T2, AC
#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e3+10;
typedef pair<int,int> PII;
int c[5], cc[5]; //上下左右
int getd(int x1, int y1, int x2, int y2)
return abs(x1-x2)+abs(y1-y2);
int main()
int n = 5;
for(int i = 1; i <= 4; i++)cin>>c[i];
for(int i = 1; i <= 4; i++)
cin>>cc[i];
// int x = cc[i];
// if(i==1||i==4)c[i]+=x;//上右
// if(i==2||i==3)c[i]-=x;//下左
vector< pair<PII,PII> >vc;
int ex, ey, d1, d2; cin>>ex>>ey>>d1>>d2;
for(int x1 = 1; x1 <= n; x1++)
for(int y1 = 1; y1 <= n; y1++)
for(int x2 = 1; x2 <= n; x2++)
for(int y2 = 1; y2 <= n; y2++)
if(getd(x1,y1,x2,y2)==d1 && getd(x2,y2,ex,ey)==d2)
//左右攻击初始位置
if(x1==c[3]-cc[3] || x1==c[4]+cc[4] || y1==c[1] || y1==c[2])
continue;
//上下攻击第一次位置
if(y2==c[1]+cc[1] || y2==c[2]-cc[2] || x2==c[3]-cc[3] || x2==c[4]+cc[4])
continue;
vc.push_back(x1,y1,x2,y2);
for(auto x : vc)
cout<<x.first.first<<" "<< x.first.second<<" "<<x.second.first<<" "<<x.second.second<<"\\n";
return 0;
3、战利品分配
在某个战争游戏中，多个玩家组成一个大型军团，攻下若干城池，并获得战利品。
具体而言，游戏中有 N 个城市，并以 M 条长度为 1 的无向道路连接，玩家们组成的军团从 S 号城市开始进攻，目的地是 T 号城市，每个城市攻下后的战利品价值为 p
i
。
为了合理地分配战利品，军团们定下了规矩：假设军团里有 K 位玩家，那么从 S 号城市开始，第 1 个攻下的城市分配给第 1 位玩家，第 2 个攻下的分配给第 2 位玩家，……，第 K 个攻下的分配给第 K 位玩家，第 K+1 个攻下的则重新开始计算，分配给第 1 位玩家，以此类推。
军团很强，路上所有的城市都可以轻松进攻下来。你作为军团的指挥，可以指定玩家的进攻路线。但玩家们都希望尽快结束游戏，因此 S 到 T 的距离必须是最短的。你需要做的是在最短距离的限制下选择对自己最好的线路，获得尽可能高的战利品价值。请输出你的答案。
输入格式:
输入第一行是四个数 N,M,K,P (1≤N,M≤10
5
,1≤K≤10
4
,1≤P≤K)，表示城市数量（于是城市从 1 到 N 编号）、连接道路数量以及你在军团中的 K 位玩家中排第 P 位（即你战利品分配在第 P 位）。
第二行是 N 个被空格隔开的非负整数，第 i 个数对应 p
i
(0≤p
i
≤10
4
)，表示编号为 i 的城市的战利品价值（i=1,⋯,N）。
然后的 M 行，每行给出两个用空格分隔的正整数 U 和 V，表示编号为 U 和 V 的城市之间有道路连接。
最后的一行是两个正整数 S,T，表示开始的城市编号与目的地的城市编号。开始和目的地的城市也是可以进攻并获取战利品的。
输出格式:
输出一行，表示你可以取得的最大价值。
输入样例:
9 11 2 2
100 150 130 50 30 20 200 0 70
1 2
1 3
2 3
2 4
2 5
3 6
4 7
5 7
6 8
7 9
8 9
1 9
输出样例:
350
- 样例图
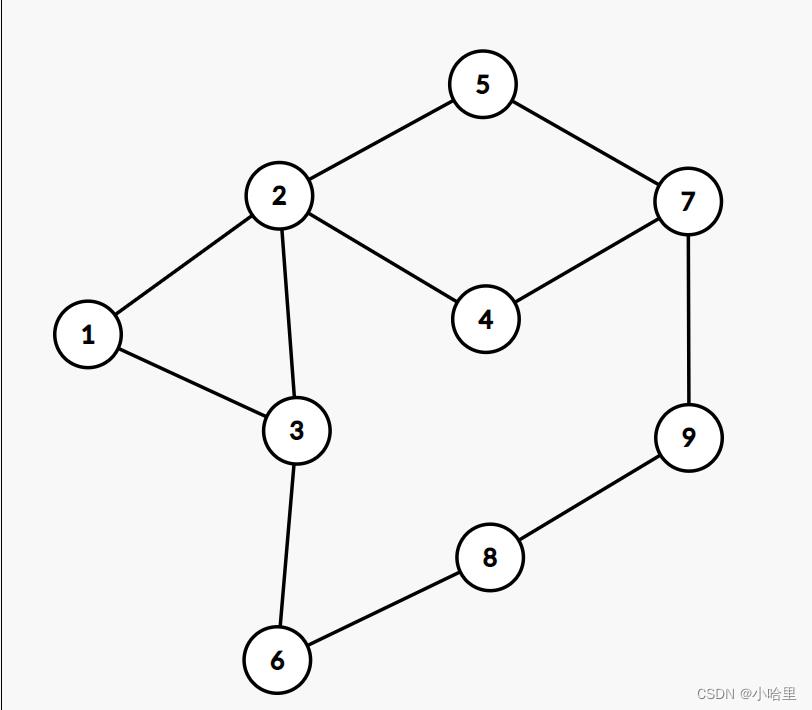
题意：
- n个点，m条权为1的无向边，从S出发到T。
- 每个点有个价值pi，军团里有K个人，你的排名为P，如果第i个走到的城市满足i%K=P，那么可以获得对应点的价值pi，求满足最短路的前提下，最大化能获得的价值。
思路：
-
乍一看S到T最短路，多维护一个最大点权，DIjkstra秒。 毕竟PTA，PAT，天梯，Robocom都喜欢出这种题，然后无脑往上敲，敲完样例没过，咋只有120
-
重新考虑一下限制条件，起点，终点固定了，最短路长度其实也固定了，也就是说，在满足上述条件的情况下，最大化中途经过的第P+i*K个点的权值之和，不考虑效率的情况下，我们可以再跑一遍bfs，统计所有路径的价值之和。
-
那么再优化一下效率，其实Dijkstra是个多余的存在，因为bfs本身也可以找最短路，所以只要跑一遍bfs，边找最短距离边记录自己沿途获得的价值即可。
-
赛后补题的时候发现我赛时写的Dijkstra是对的（无语了，绕了一大圈重写bfs）。
单个Dijk其实跟bfs一样，多维护一个数组表示到达i能拿到的最大价值即可，转移的时候一起更新即可。 当时错是因为初始值 考虑第i个点而不是第i条边时，起点步数初始化没改成1，所以WA的。。。ohhh是我sb
//3, Dij, AC
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int>PII;
const int maxn = 1e5+10, inf = 1e9+7;
int n, m, k, p, w[maxn];
int check(int x) return (x>=p && (x-p)%k==0); //当前这步是拿得到的
vector<int>G[maxn];
int st, ed;
int dist[maxn], vis[maxn];
int dd[maxn]; //维护到第i个点位置能拿到的最大价值
void Dijkstra()
for(int i = 0; i <= n; i++)dist[i] = inf; vis[i] = 0;
dist[st] = 1; //WA：因为是第i个点，不是边，所以起点要+1，（赛时1分版）
priority_queue<PII,vector<PII>, greater<PII> > q;
q.push(1,st);
while(!q.empty())
PII t = q.top(); q.pop();
if(vis[t.second])continue;
vis[t.second] = 1;
for(int to : G[t.second])
if(dist[to] > dist[t.second]+1)
dist[to] = dist[t.second]+1;
if(check(dist[to]))dd[to] = dd[t.second]+w[to];
else dd[to] = dd[t.second];
q.push(dist[to],to);
else if(dist[to] == dist[t.second]+1)
if(dd[t.second]>dd[to])
dd[to] = dd[t.second];
q.push(dist[to],to);
int main()
cin>>n>>m>>k>>p;
for(int i = 1; i <= n; i++)cin>>w[i];
for(int i = 1; i <= m; i++)
int u,v ; cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
cin>>st>>ed;
Dijkstra();
if(p==1)dd[ed] += w[st]; //p==1的时候，可以多拿到一个起点的价值
cout<<dd[ed]<<'\\n';
return 0;
//3, Dij+bfs, AC
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int>PII;
const int maxn = 1e5+10, inf = 1e9+7;
int n, m, k, p, w[maxn];
//Dijkstra找最短路
vector<int>G[maxn];
int st, ed, dist[maxn], vis[maxn];
void Dijkstra()
for(int i = 0; i <= n; i++)dist[i] = inf; vis[i] = 0;
dist[st] = 1;
priority_queue<PII,vector<PII>, greater<PII> > q;
q.push(0,st);
while(!q.empty())
PII t = q.top(); q.pop();
if(vis[t.second])continue;
vis[t.second] = 1;
for(int to : G[t.second])
if(dist[to] > dist[t.second]+1)
dist[to] = dist[t.second]+1;
q.push(dist[to],to);
//bfs找最大价值
int val[maxn]; //到点i的最大价值
void bfs()
for(int i = 0; i <= n; i++)val[i] = -inf; vis[i] = 0;
queue<int>q;
q.push(st);
val[st] = 0; vis[st] = 1;
while(q.size())
int t = q.front(); q.pop();
if(dist[t]>=p && (dist[t]-p)%k==0)
val[t] += w[t];
if(t==ed)break;
for(int to : G[t])
if(dist[to]>dist[t] && val[to]<val[t])
val[to] = val[t];
if(!vis[to])
vis[to] = 1;
q.push(to);
int main()
cin>>n>>m>>k>>p;
for(int i = 1; i <= n; i++)cin>>w[i];
for(int i = 1; i <= m; i++)
int u,v ; cin>>以上是关于2022 RoboCom 世界机器人开发者大赛-本科组（国赛）的主要内容，如果未能解决你的问题，请参考以下文章
2021 RoboCom 世界机器人开发者大赛-本科组（初赛）
2021 RoboCom 世界机器人开发者大赛-本科组（初赛）
2021 RoboCom 世界机器人开发者大赛-本科组（初赛）完结
2021 RoboCom 世界机器人开发者大赛-本科组（复赛）