《机器学习实战》使用Apriori算法和FP-growth算法进行关联分析(Python版)
Posted 搜索与推荐Wiki
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了《机器学习实战》使用Apriori算法和FP-growth算法进行关联分析(Python版)相关的知识,希望对你有一定的参考价值。
=====================================================================
《机器学习实战》系列博客是博主阅读《机器学习实战》这本书的笔记也包含一些其他python实现的机器学习算法 算法实现均采用pythongithub 源码同步:https://github.com/Thinkgamer/Machine-Learning-With-Python
=====================================================================
1:关联分析
2:Apriori算法和FP-growth算法原理
3:使用Apriori算法发现频繁项集
4:使用FP-growth高效发现频繁项集
5:实例:从新闻站点点击流中挖掘新闻报道
以下程序用到的源代码下载地址:GitHub点击查看
一:关联分析
1:相关概念
关联分析(association analysis):从大规模数据集中寻找商品的隐含关系
项集 (itemset):包含0个或者多个项的集合称为项集
频繁项集:那些经常一起出现的物品集合
支持度计数(support count):一个项集出现的次数也就是整个交易数据集中包含该项集的事物数
关联规则是形如A->B的表达式,规则A->B的度量包括支持度和置信度
项集支持度:一个项集出现的次数与数据集所有事物数的百分比称为项集的支持度
eg:support(A->B)=support_count(A并B) / N
项集置信度(confidence):数据集中同时包含A,B的百分比
eg:confidence(A->B) = support_count(A并B) / support_count(A)
2:关联分析一些应用
(1):购物篮分析,通过查看那些商品经常在一起出售,可以帮助商店了解用户的购物行为,这种从数据的海洋中抽取只是可以用于商品定价、市场促销、存货管理等环节
(2):在Twitter源中发现一些公共词。对于给定的搜索词,发现推文中频繁出现的单词集合
(3):从新闻网站点击流中挖掘新闻流行趋势,挖掘哪些新闻广泛被用户浏览到
(4):搜索引擎推荐,在用户输入查询时推荐同时相关的查询词项
(5):发现毒蘑菇的相似特征。这里只对包含某个特征元素(有毒素)的项集感兴趣,从中寻找毒蘑菇中的一些公共特征,利用这些特征来避免迟到哪些有毒的蘑菇
3:样例(下文分析所依据的样本,交易数据表)
| 交易号码 | 商品 |
| 100 | Cola,Egg,Ham |
| 200 | Cola,Diaper,Beer |
| 300 | Cola,Diaper,Beer,Ham |
| 400 | Diaper,Beer |
二:Apriori算法和FP-growth算法原理
1:Apriori算法原理
找出所有可能是频繁项集的项集,即候选项集,然后根据最小支持度计数删选出频繁项集,最简单的办法是穷举法,即把每个项集都作为候选项集,统计他在数据集中出现的次数,如果出现次数大于最小支持度计数,则为频繁项集。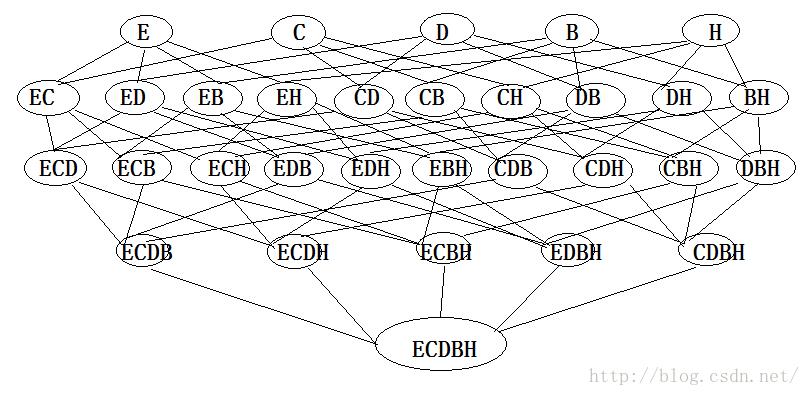
所有的可能的项集(E:Egg C:Cola D:Diaper B:Beer H:Ham)
频繁项集的发现过程如下(假定给定的最小支持度为2):
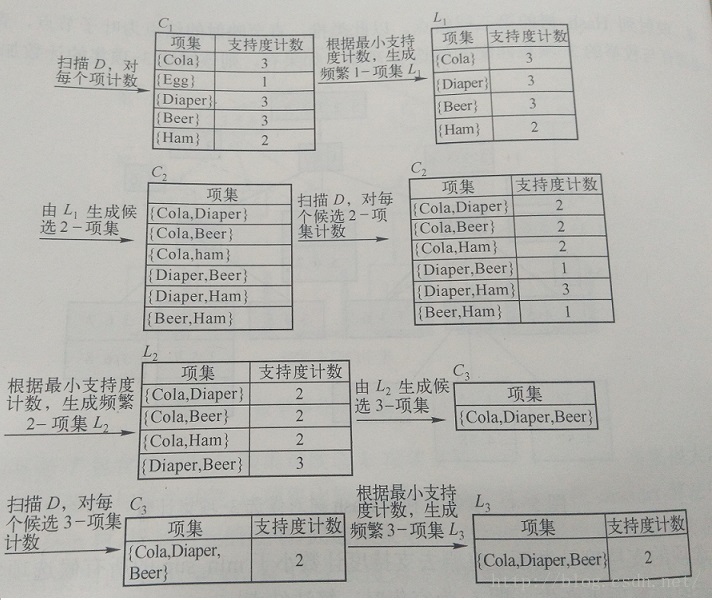
经过剪枝后的图为(红色圆圈内即为剪枝去掉的部分):
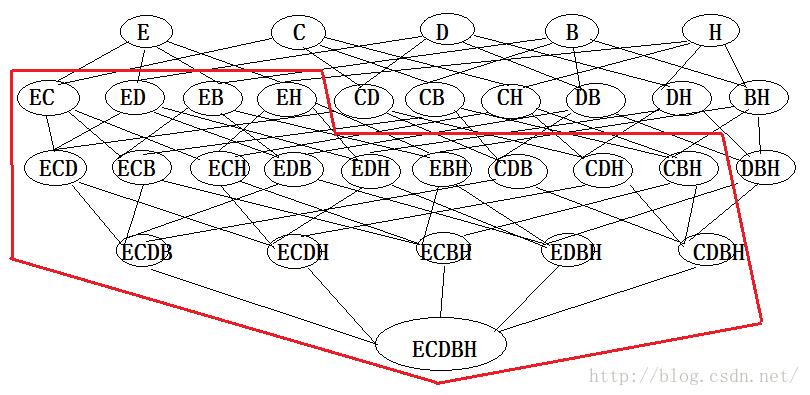
剪枝后的候选集为(E:Egg C:Cola D:Diaper B:Beer H:Ham)
那么CD,CB,CH,DB,DH,BH,DBH即为所求的候选集
2:FP-growth算法原理
FP-growth算法不同于Apriori算法生成候选项集再检查是否频繁的”产生-测试“方法,而是使用一种称为频繁模式树(FP-Tree,PF代表频繁模式,Frequent Pattern)菜单紧凑数据结构组织数据,并直接从该结构中提取频繁项集,下面针对
| 交易号码 | 商品 |
| 100 | Cola,Egg,Ham |
| 200 | Cola,Diaper,Beer |
| 300 | Cola,Diaper,Beer,Ham |
| 400 | Diaper,Beer |
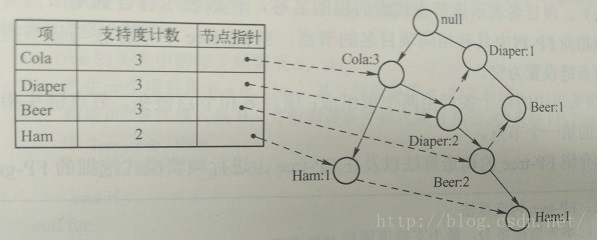
三:使用Apriori算法发现频繁项集和挖掘相关规则
1:发现频繁项集
Apriori算法是发现频繁项集的一种方法。Apriori算法的两个输入参数分别是最小支持度和数据集。该算法首先会生成所有单个元素的项集列表。接着扫描数据集来查看哪些项集满足最小支持度要求,那些不满足最小支持度的集合会被去掉。然后,对剩下来的集合进行组合以生成包含两个元素的项集。接下来,再重新扫描交易记录,去掉不满足最小支持度的项集。该过程重复进行直到所有项集都被去掉,创建 Apriori.py文件,加入以下代码
@author: Gamer Think ''' from pydoc import apropos #========================= 准备函数 (下) ========================================== #加载数据集 def loadDataSet(): return [[1,3,4],[2,3,5],[1,2,3,5],[2,5]] def createC1(dataSet): C1 = [] #C1为大小为1的项的集合 for transaction in dataSet: #遍历数据集中的每一条交易 for item in transaction: #遍历每一条交易中的每个商品 if not [item] in C1: C1.append([item]) C1.sort() #map函数表示遍历C1中的每一个元素执行forzenset,frozenset表示“冰冻”的集合,即不可改变 return map(frozenset,C1) #Ck表示数据集,D表示候选集合的列表,minSupport表示最小支持度 #该函数用于从C1生成L1,L1表示满足最低支持度的元素集合 def scanD(D,Ck,minSupport): ssCnt = for tid in D: for can in Ck: #issubset:表示如果集合can中的每一元素都在tid中则返回true if can.issubset(tid): #统计各个集合scan出现的次数,存入ssCnt字典中,字典的key是集合,value是统计出现的次数 if not ssCnt.has_key(can): ssCnt[can] = 1 else: ssCnt[can] += 1 numItems = float(len(D)) retList = [] supportData = for key in ssCnt: #计算每个项集的支持度,如果满足条件则把该项集加入到retList列表中 support = ssCnt[key]/numItems if support >= minSupport: retList.insert(0, key) #构建支持的项集的字典 supportData[key] = support return retList,supportData #==================== 准备函数(上) ============================= #====================== Apriori算法(下) ================================= #Create Ck,CaprioriGen ()的输人参数为频繁项集列表Lk与项集元素个数k,输出为Ck def aprioriGen(Lk,k): retList = [] lenLk = len(Lk) for i in range(lenLk): for j in range(i+1,lenLk): #前k-2项相同时合并两个集合 L1 = list(Lk[i])[:k-2] L2 = list(Lk[j])[:k-2] L1.sort() L2.sort() if L1 == L2: retList.append(Lk[i] | Lk[j]) return retList def apriori(dataSet, minSupport=0.5): C1 = createC1(dataSet) #创建C1 #D: [set([1, 3, 4]), set([2, 3, 5]), set([1, 2, 3, 5]), set([2, 5])] D = map(set,dataSet) L1,supportData = scanD(D, C1, minSupport) L = [L1] #若两个项集的长度为k - 1,则必须前k-2项相同才可连接,即求并集,所以[:k-2]的实际作用为取列表的前k-1个元素 k = 2 while(len(L[k-2]) > 0): Ck = aprioriGen(L[k-2], k) Lk,supK = scanD(D,Ck, minSupport) supportData.update(supK) L.append(Lk) k +=1 return L,supportData #====================== Apriori算法(上) ================================= if __name__=="__main__": dataSet = loadDataSet() L,suppData = apriori(dataSet) i = 0 for one in L: print "项数为 %s 的频繁项集:" % (i + 1), one,"\\n" i +=1 |

2:挖掘相关规则
要找到关联规则,我们首先从一个频繁项集开始。从文章开始说的那个交易数据表的例子可以得到,如果有一个频繁项集Diaper,Beer,那么就可能有一条关联规则“Diaper➞Beer”。这意味着如果有人购买了Diaper,那么在统计上他会购买Beer的概率较大。注意这一条反过来并不总是成立,也就是说,可信度(“Diaper➞Beer”)并不等于可信度(“Beer➞Diaper”)。前文也提到过,一条规则P➞H的可信度定义为support(P 并 H)/support(P)。可见可信度的计算是基于项集的支持度的。
下图给出了从项集0,1,2,3产生的所有关联规则,其中阴影区域给出的是低可信度的规则。可以发现如果0,1,2➞3是一条低可信度规则,那么所有其他以3作为后件(箭头右部包含3)的规则均为低可信度的。
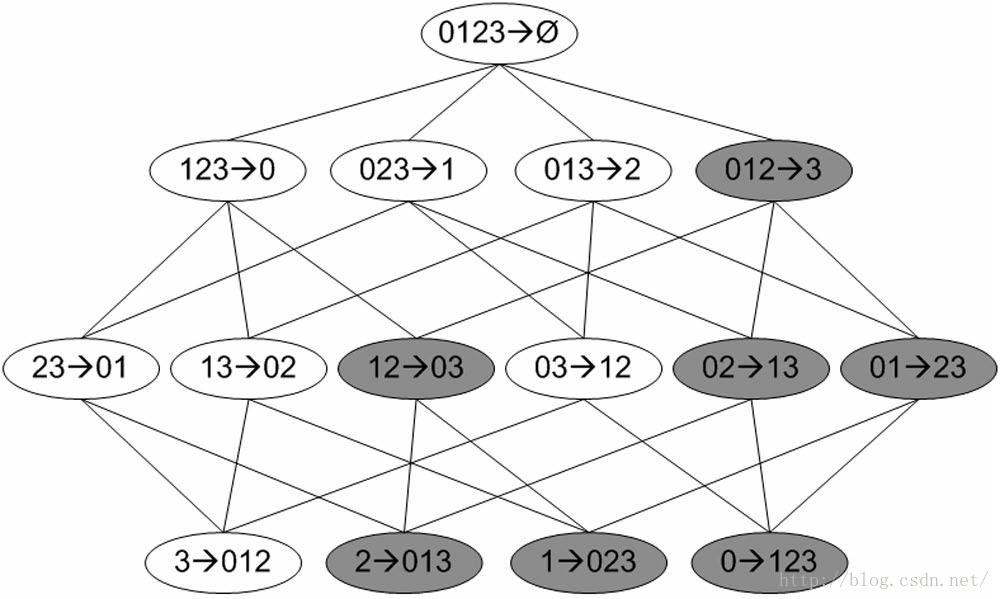
频繁项集0,1,2,3的关联规则网格示意图
可以观察到,如果某条规则并不满足最小可信度要求,那么该规则的所有子集也不会满足最小可信度要求。以图4为例,假设规则0,1,2 ➞ 3并不满足最小可信度要求,那么就知道任何左部为0,1,2子集的规则也不会满足最小可信度要求。可以利用关联规则的上述性质属性来减少需要测试的规则数目,类似于Apriori算法求解频繁项集。
关联规则生成函数:
def generateRules(L, supportData, minConf=0.7):
bigRuleList = []
for i in range(1, len(L)):
for freqSet in L[i]:
H1 = [frozenset([item]) for item in freqSet]
if (i > 1):
# 三个及以上元素的集合
rulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf)
else:
# 两个元素的集合
calcConf(freqSet, H1, supportData, bigRuleList, minConf)
return bigRuleList
|
这个函数是主函数,调用其他两个函数。其他两个函数是rulesFromConseq()和calcConf(),分别用于生成候选规则集合以及对规则进行评估(计算支持度)。
函数generateRules()有3个参数:频繁项集列表L、包含那些频繁项集支持数据的字典supportData、最小可信度阈值minConf。函数最后要生成一个包含可信度的规则列表bigRuleList,后面可以基于可信度对它们进行排序。L和supportData正好为函数apriori()的输出。该函数遍历L中的每一个频繁项集,并对每个频繁项集构建只包含单个元素集合的列表H1。代码中的i指示当前遍历的频繁项集包含的元素个数,freqSet为当前遍历的频繁项集(回忆L的组织结构是先把具有相同元素个数的频繁项集组织成列表,再将各个列表组成一个大列表,所以为遍历L中的频繁项集,需要使用两层for循环)。
辅助函数——计算规则的可信度,并过滤出满足最小可信度要求的规则
def calcConf(freqSet, H, supportData, brl, minConf=0.7):
''' 对候选规则集进行评估 '''
prunedH = []
for conseq in H:
conf = supportData[freqSet] / supportData[freqSet - conseq]
if conf >= minConf:
print freqSet - conseq, '-->', conseq, 'conf:', conf
brl.append((freqSet - conseq, conseq, conf))
prunedH.append(conseq)
return prunedH
|
计算规则的可信度以及找出满足最小可信度要求的规则。函数返回一个满足最小可信度要求的规则列表,并将这个规则列表添加到主函数的bigRuleList中(通过参数brl)。返回值prunedH保存规则列表的右部,这个值将在下一个函数rulesFromConseq()中用到。
辅助函数——根据当前候选规则集H生成下一层候选规则集
def rulesFromConseq(freqSet, H, supportData, brl, minConf=0.7):
''' 生成候选规则集 '''
m = len(H[0])
if (len(freqSet) > (m + 1)):
Hmpl = aprioriGen(H, m + 1)
Hmpl = calcConf(freqSet, Hmpl, supportData, brl, minConf)
if (len(Hmpl) > 1):
rulesFromConseq(freqSet, Hmpl, supportData, brl, minConf)
|
从最初的项集中生成更多的关联规则。该函数有两个参数:频繁项集freqSet,可以出现在规则右部的元素列表H。其余参数:supportData保存项集的支持度,brl保存生成的关联规则,minConf同主函数。函数先计算H中的频繁项集大小m。接下来查看该频繁项集是否大到可以移除大小为m的子集。如果可以的话,则将其移除。使用函数aprioriGen()来生成H中元素的无重复组合,结果保存在Hmp1中,这也是下一次迭代的H列表。
将上边的三个函数加入 Apriori.py中main函数修改为:
|
if __name__=="__main__":
dataSet = loadDataSet()
L,suppData = apriori(dataSet)
i = 0
for one in L:
print "项数为 %s 的频繁项集:" % (i + 1), one,"\\n"
i +=1
print "minConf=0.7时:" rules = generateRules(L,suppData, minConf=0.7) print "\\nminConf=0.5时:" rules = generateRules(L,suppData, minConf=0.5) |
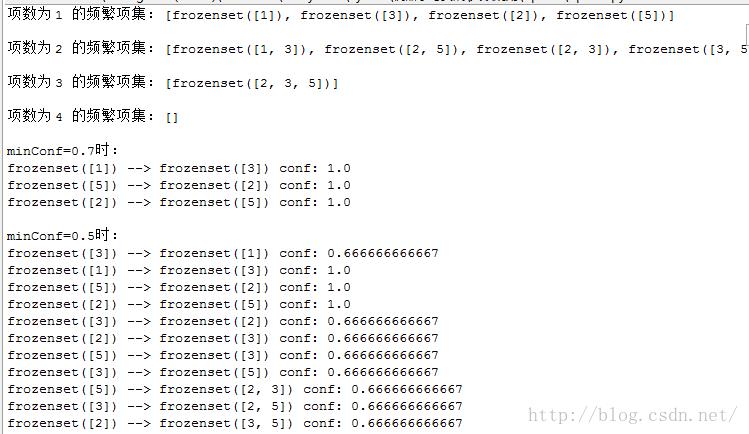
如果仔细看下上述代码和输出,会发现这里面是一些问题的。
1 问题的提出
频繁项集L的值前面提到过。我们在其中计算通过2, 3, 5生成的关联规则,可以发现关联规则3, 5➞2和2, 3➞5的可信度都应该为1.0的,因而也应该包括在当minConf = 0.7时的rules中——但是这在前面的运行结果中并没有体现出来。minConf = 0.5时也是一样,3, 5➞2的可信度为1.0,2, 5➞3的可信度为2/3,2, 3➞5的可信度为1.0,也没有体现在rules中。
通过分析程序代码,我们可以发现:
- 当i = 1时,generateRules()函数直接调用了calcConf()函数直接计算其可信度,因为这时L[1]中的频繁项集均包含两个元素,可以直接生成和判断候选关联规则。比如L[1]中的2, 3,生成的候选关联规则为2➞3、3➞2,这样就可以了。
- 当i > 1时,generateRules()函数调用了rulesFromConseq()函数,这时L[i]中至少包含3个元素,如2, 3, 5,对候选关联规则的生成和判断的过程需要分层进行(图4)。这里,将初始的H1(表示初始关联规则的右部,即箭头右边的部分)作为参数传递给了rulesFromConseq()函数。
例如,对于频繁项集a, b, c, …,H1的值为[a, b, c, …](代码中实际为frozenset类型)。如果将H1带入计算可信度的calcConf()函数,在函数中会依次计算关联规则b, c, d, …➞a、a, c, d, …➞b、a, b, d, …➞c……的支持度,并保存支持度大于最小支持度的关联规则,并保存这些规则的右部(prunedH,即对H的过滤,删除支持度过小的关联规则)。
当i > 1时没有直接调用calcConf()函数计算通过H1生成的规则集。在rulesFromConseq()函数中,首先获得当前H的元素数m = len(H[0])(记当前的H为Hm )。当Hm可以进一步合并为m+1元素数的集合Hm+1时(判断条件:len(freqSet) > (m + 1)),依次:
- 生成Hm+1:Hmpl = aprioriGen(H, m + 1)
- 计算H