计算机图形学输出图元_10_多边形填充区_2_分割凹多边形

Posted 2022-08-18 heyuchang666

分割凹多边形

       一旦识别出凹多边形，我们可以将它切割成一组凸多边形。这可使用边向量和边叉积来完成。我们可以利用顶点和边延长线的关系来确定哪些顶点在其一侧，哪些顶点在另一侧。在下面的算法中我们假定所有多边形均在xy平面上。当然，在世界坐标系中描述的多边形的初始位置可能不在xy平面上，但我们可以使用第5章的讨论的变换方法将它们移到xy平面上。对于分割凹多边形的向量方法(vector method)，我们首先要形成边向量。给定相继的向量位置V_k和V_k+1定义边向量:

 

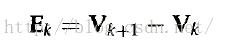
       接着按多边形边界顺序计算连续的边向量的叉积。如果有些叉积的z分量为正而另一些为负，则多边形为凹多边形；否则，多边形为凸多边形。这意味着不存在三个连续的顶点共线，即不存在连续两个边向量其叉积为0。如果所有顶点共线，则得到一个退化多边形(一条线段)。我们可以通过逆时针方向处理边向量来应用向量方法。如果有一个叉积的z分量为负值(如图3.43所示)，那么多边形为凹且可沿叉积中第一边向量的直线进行切割。下面的例子给出了分割凹多边形的这一方法。

例3.4分割凹多边形的向量方法

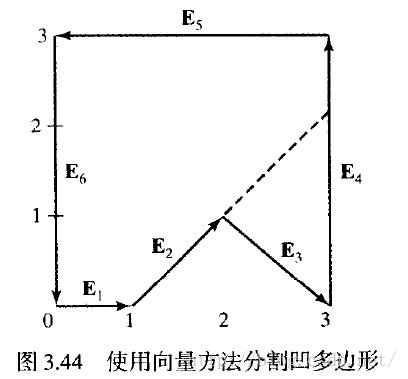
图3.44给出了一个有6个顶点的凹多边形。该多边形的边向量表示为

 

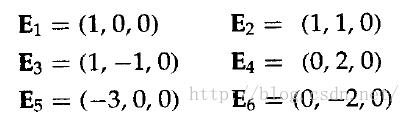
这里的z分量均为0，因为所有边均在xy平面上。两个连续的边向量的叉积E_jx E_k是垂直于xy平面的向量，其分量等E_jxE_ky- E_kxE_jy:

 

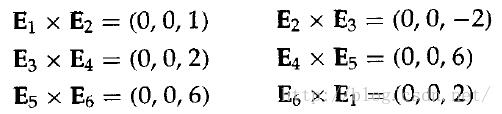
        因为叉积E2 x E3的z分量为负，我们沿向量E2的直线分割多边形。该边的直线方程中的斜率为1而y轴截距为-1。然后我们可以确定这条直线和其他边的交点来将多边形分割成两片。其他边又积不为负，所以得到的两个多边形均为凸多边形。

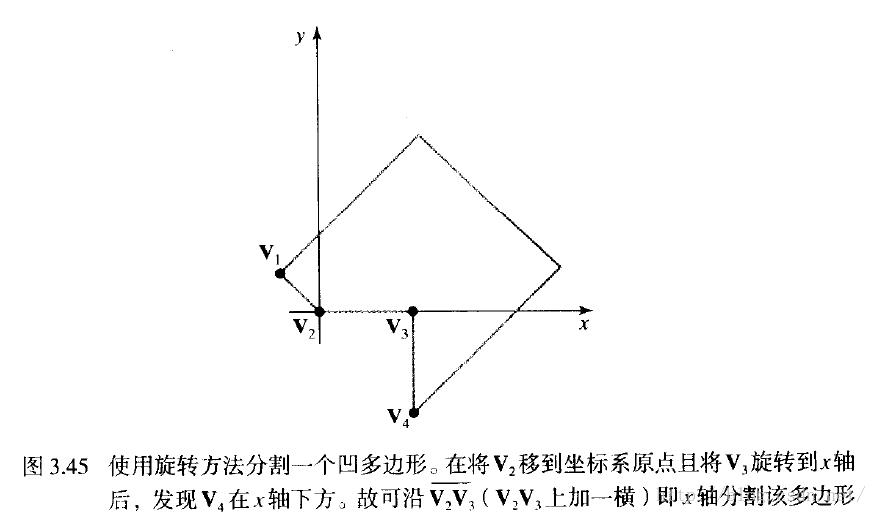
       我们还可以使用旋转法(rotational method)来分割凹多边形。沿多边形的边的逆时针方向，逐一将顶点V_k移到坐标系原点。然后顺时针旋转多边形，使下一顶点V_k+1落在x轴上。如果再下一个顶点V_k+2位于x轴下面，则多边形为凹。然后我们利用x轴将多边形分割成两个新多边形，并对这两个新多边形重复使用凹测试。上述步骤一直重复到多边形中所有顶点均经过测试。对象位置旋转和平移的方法将在第5章讨论。图3.45给出了分割凹多边形的旋转法。

 

将凸多边形分割成三角形集

      一旦有了一个凸多边形的顶点集，我们可以将其变成一组三角形。这通过将任意顺序的三个连续顶点定义为一个新多边形(三角形)来实现。然后将三角形的中间顶点从多边形原顶点队列中删除。接着使用相同的过程处理修改后的顶点队列来分出另一个三角形。这种分割一直进行到原多边形仅留下三个顶点，它们定义三角形集中的最后一个。凹多边形也可以使用这种方法分割为三角形集，但要求每次三顶点形成的内角小于180^o(一个“凸”角)。