深度优先与广度优先
Posted createchance
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了深度优先与广度优先相关的知识,希望对你有一定的参考价值。
文章转载自:http://blog.csdn.net/a45872055555/article/details/37543795
今天做了道题目,《手机键盘输入》当按下23时,输出[“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”]。
其实说白了,也就是全排列问题,将2代表的abc,和3代表的def输出组合的字符。
我是按照普通方法,递归来写的,觉得这道题目也只是考验编程,考验递归的。没太多考虑,当上网看别人都提到DFS(深度优先算法)后,才意识到,是有章法可循的。以前只以为深度优先和广度优先只是在图的遍历的时候才能用到,想不到这些也只是工具,看你怎么去应用到你的算法里面。
好了,不多说了,基于上述原因,参考《数据结构》和《算法导论》将广度优先和深度优先总结一下。
这两个算法的共同点,都是要有标记!数据结构采用的是一个数组来标记每一个结点是否被遍历;算法导论是在结点中附设一个颜色值,来表示遍历的程度。其实质是一样的,都需要借助于标记,来实现。但在二叉树的遍历中就不需要了,因为不会形成回路。
一:深度优先算法
方案一:“数据结构”
其实这是树的先根遍历的扩展。

通过图(b)我们可以看到,v1-v4-v8-v5-v3-v6-v7。
只要遍历到某一个结点,有子节点就先遍历子节点,当“子树”遍历完了以后,再遍历另一个“子树”,只是由于存在回路,所以遍历另一个子树的时候,会访问已经访问过的点, 所以就需要标记来判断。
代码如下:
[cpp] view plain copy print ?
- Boolean visited[MAX]; //设置标志数组
- Status (*VisitFunc)(int v); //全局变量函数,方便在DFS中调用DFSTraverse中传进的参数
- void DFSTraverse(Graph G,Status (*Visit)(int v))
- VisitFunc = Visit;
- for(v = 0;v < G.vexnum;++v) //初始化,将标志数组全设为FALSE
- visited[v] = FALSE;
- for(v = 0;v < G.vexnum;++v) //对所有的结点进行遍历,找到切入点,就调用DFS进行深度优先遍历
- if(!visited[v])
- DFS(G,v);
- void DFS(Graph G,int v)
- visited[v] = TRUE; //给第v个结点标记,并访问该结点。
- VisitFunc(v);
- for(w = FirstAdjVex(G,v); w >= 0;w = NextAdjVex(G,v,w)) //对v的所有子节点w进行深度优先遍历
- if(!visited[w])
- DFS(G,w);

Boolean visited[MAX]; //设置标志数组
Status (*VisitFunc)(int v); //全局变量函数,方便在DFS中调用DFSTraverse中传进的参数
void DFSTraverse(Graph G,Status (*Visit)(int v))
VisitFunc = Visit;
for(v = 0;v < G.vexnum;++v) //初始化,将标志数组全设为FALSE
visited[v] = FALSE;
for(v = 0;v < G.vexnum;++v) //对所有的结点进行遍历,找到切入点,就调用DFS进行深度优先遍历
if(!visited[v])
DFS(G,v);
void DFS(Graph G,int v)
visited[v] = TRUE; //给第v个结点标记,并访问该结点。
VisitFunc(v);
for(w = FirstAdjVex(G,v); w >= 0;w = NextAdjVex(G,v,w)) //对v的所有子节点w进行深度优先遍历
if(!visited[w])
DFS(G,w);
说明:
1:这个题目写的很简化,在visited[v]中v是一个确定的数值,表示数组下标。但在VisitFunc(v)中,v为结点。虽然程序写法简化,但更能突出我们要解决的问题。
2:其实DFS和二叉树的先序遍历很相像:
[cpp] view plain copy print ?
- visit(p);
- PreOrderTraverse(p->left);
- PreOrderTraverse(p->right);

visit(p);
PreOrderTraverse(p->left);
PreOrderTraverse(p->right);
其实就是将二叉树的确定性,转化成图子节点的不确定性,通过for循环来实现。
3:DFS可以应用在树的先序遍历当中。
方案二:“算法导论”
1:遍历过程
只要可能,就在图中尽量深入,总是对最近发现的结点v的出发边进行探索,直到该结点的所有出发边都被发现为止。然后回溯到v的父节点(可能有多个,但之前遍历过程中,从哪个点过来的,就是v的父节点),然后搜索该前驱结点的出发边。知道从源节点可以达到的所有的出发边都遍历完。如果在图中还有没被遍历的结点, 任选一个,重复上述过程。直到所有的结点遍历完为止。
2:当发现一个结点v时,记录其前驱结点u,并设置父节点指针v.π = u; 同样设置三种颜色,白色表示尚未被遍历的结点,灰色表示已经被遍历,但其子节点还没有被遍历完全,黑色表示该结点以及所有的子节点都被遍历完全,要返回到父节点。
3:给每个结点设置时间戳。v.d记录第一次被发现的时间,v.f记录对v扫描完成时的时间戳。其中time为全局变量
代码:
[cpp] view plain copy print ?
- DFS(G)
- for(u = 0;u < G.vexnum;++u) //初始化所有的结点信息,父指针设为空,颜色全为白色
- u.color = WHITE;
- u.π = NULL;
- time = 0;
- for(u = 0;u < G.vexnum;++u) //开始遍历所有的结点,以防存在多个不相接的图
- if(u.color == WHITE)
- DFS_VISIT(G,u);
- DFS_VISIT(G,u)
- time = time + 1; //每次赋值前都要增加1,time为全局变量
- u.d = time;
- u.color = GRAY; //当访问了该结点,就将该节点设为灰色,接下来遍历其子节点。其实不要该灰色指示也行
- for(w = FirstAdjVex(G,v); w >= 0;w = NextAdjVex(G,v,w)) //处理子节点
- if(w.color == WHITE)
- w.π = u;
- DFS_VISIT(G,w);
- u.color = BLACK;
- time = time + 1;
- u.f = time;

DFS(G)
for(u = 0;u < G.vexnum;++u) //初始化所有的结点信息,父指针设为空,颜色全为白色
u.color = WHITE;
u.π = NULL;
time = 0;
for(u = 0;u < G.vexnum;++u) //开始遍历所有的结点,以防存在多个不相接的图
if(u.color == WHITE)
DFS_VISIT(G,u);
DFS_VISIT(G,u)
time = time + 1; //每次赋值前都要增加1,time为全局变量
u.d = time;
u.color = GRAY; //当访问了该结点,就将该节点设为灰色,接下来遍历其子节点。其实不要该灰色指示也行
for(w = FirstAdjVex(G,v); w >= 0;w = NextAdjVex(G,v,w)) //处理子节点
if(w.color == WHITE)
w.π = u;
DFS_VISIT(G,w);
u.color = BLACK;
time = time + 1;
u.f = time;
生成的图
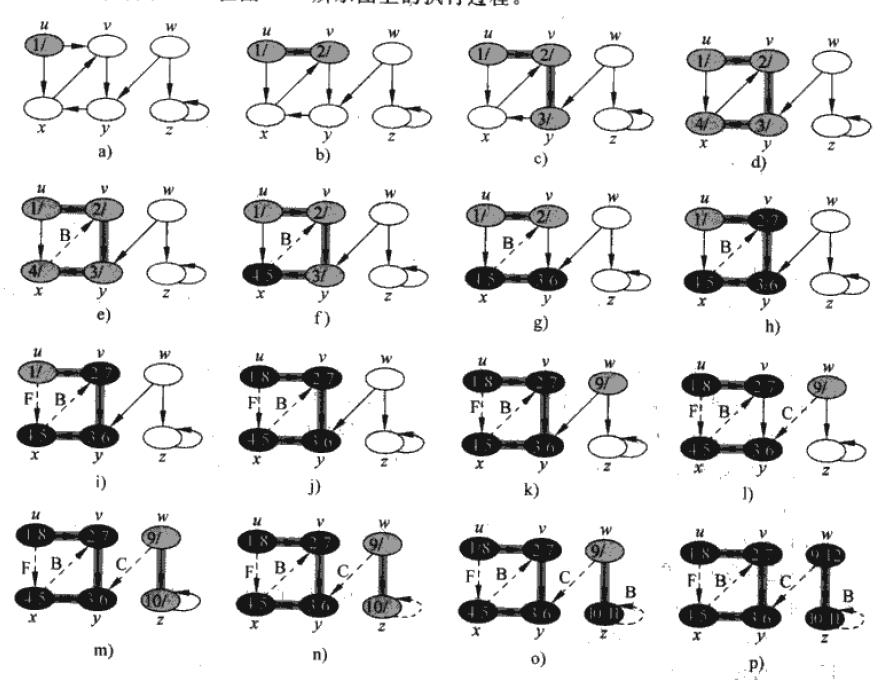
性质:
1、其生成的前驱制图G形成一个由多棵树所构成的森林,这是因为深度优先树的结构与DFS_VISIT的递归调用结构完全对应。
2、结点的发现时间和完成时间具有括号化结构。也就是只要两个结点的时间有重叠,毕竟一个结点的时间段包含在另一个结点的时间段内。
二:广度优先搜索
类似于树的按层次遍历的过程。
方案一:“数据结构”
先访问根结点,然后访问与跟相连的所有结点v1-vn,然后访问与v1-vn直接相连的所有结点(除去已经访问过的结点)。这就要用队列来时间:先访问某结点,然后将该结点如队列。从队列出结点,然后依次访问该结点的所有子节点(除去已经访问过的结点),并将这些刚刚访问结点入队列(这样将提前访问过的结点就不用入队列了,其子节点已经提前放入队列当中)。

访问过程是:v1-v2-v3-v4-v5-v6-v7-v8。

- void BFSTraverse(Graph G,Status(*Visit)(int v))
- for(u = 0;u < G.vexnum;++u) //初始化
- visited[u] = FALSE;
- InitQueue(Q);
- for(v = 0;v < G.vexnum;++v) //遍历所有的结点
- if(!visited[v])
- visited[v] = TRUE;
- Visit(v); //先访问再入队列
- EnQueue(Q,v);
- while(!QueueEmpty(Q))
- DeQueue(Q,u);
- for(w = FirstAdjVex(G,v); w >= 0;w = NextAdjVex(G,v,w))
- if(!visited[w])
- visited[w] = TRUE;
- Visit(w);
- EnQueue(Q,w);

void BFSTraverse(Graph G,Status(*Visit)(int v))
for(u = 0;u < G.vexnum;++u) //初始化
visited[u] = FALSE;
InitQueue(Q);
for(v = 0;v < G.vexnum;++v) //遍历所有的结点
if(!visited[v])
visited[v] = TRUE;
Visit(v); //先访问再入队列
EnQueue(Q,v);
while(!QueueEmpty(Q))
DeQueue(Q,u);
for(w = FirstAdjVex(G,v); w >= 0;w = NextAdjVex(G,v,w))
if(!visited[w])
visited[w] = TRUE;
Visit(w);
EnQueue(Q,w);
方案二:“算法导论”
该算法可以得到最短路径。
[cpp] view plain copy print ?
- BFS(G,s)
- for(u = 0;u < G.vexnum;++u)
- u.color = WHITE;
- u.d = 10000;
- u.π = NULL;
- s.color = GRAY;
- s.d = 0;
- s.π = NULL;
- Q = 空
- EnQueue(Q,s);
- while(!IsEmpty(Q))
- u = DeQueue(Q);
- for(w = FirstAdjVex(G,v); w >= 0;w = NextAdjVex(G,v,w))
- if(w.color == WHITE)
- w.color = GRAY;
- w.d = u.d + 1;
- w.π = u;
- EnQueue(Q,w);
- u.color = BLACK;

BFS(G,s)
for(u = 0;u < G.vexnum;++u)
u.color = WHITE;
u.d = 10000;
u.π = NULL;
s.color = GRAY;
s.d = 0;
s.π = NULL;
Q = 空
EnQueue(Q,s);
while(!IsEmpty(Q))
u = DeQueue(Q);
for(w = FirstAdjVex(G,v); w >= 0;w = NextAdjVex(G,v,w))
if(w.color == WHITE)
w.color = GRAY;
w.d = u.d + 1;
w.π = u;
EnQueue(Q,w);
u.color = BLACK;
遍历后的图形:

因为我们有设置父节点指针,当通过广度优先遍历之后,我们从要找的叶节点反向遍历到根结点,就能得到最短的路径。

- PRINT_PATH(G,s,v)
- if(v == s)
- print s;
- else if(v.π == NULL)
- print ”no path form”s“to”v
- else
- PRINT_PATH(G,s,v.π)
- print v;

PRINT_PATH(G,s,v)
if(v == s)
print s;
else if(v.π == NULL)
print "no path form"s"to"v
else
PRINT_PATH(G,s,v.π)
print v;
以上是关于深度优先与广度优先的主要内容,如果未能解决你的问题,请参考以下文章