“蔚来杯“2022牛客暑期多校训练营5,签到题KBGHFCD
Posted 小哈里
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了“蔚来杯“2022牛客暑期多校训练营5,签到题KBGHFCD相关的知识,希望对你有一定的参考价值。
A Don’t Starve 点击查看 138/1324
B Watches 点击查看 1554/5695
C Bit Transmission 点击查看 1336/5774
D Birds in the tree 点击查看 174/580
E Fraction Game 点击查看 30/168
F A Stack of CDs 点击查看 750/2021
G KFC Crazy Thursday 点击查看 1281/2633
H Cutting Papers 点击查看 1252/2239
I Board Game 点击查看 20/393
J Check In 点击查看 0/43
K Headphones 点击查看 1617/3849
文章目录
K.Headphones
链接:https://ac.nowcoder.com/acm/contest/33190/K
来源:牛客网
题目描述
One day, NIO’s home is out of power. So Nio and his sister, Yasa, wanted to take some headphones from the drawer. In the dark, If they randomly took some headphones, and Yasa had taken out kk pairs of headphones. How many headphones NIO should take to make sure that he get more pairs than his sister, i.e., k+1k+1 pairs of headphones. Assume that there are NN pairs of headphones in the drawer, and each pair is different from another.
输入描述:
There are multiple test cases.
For each test case, input two integers NN and kk , representing the number of the total number of pairs in the drawer and the number of pairs Yasa had taken.
If it cannot guarantee that NIO will get more pairs of headphones than his sister, output -1.
1\\leq k \\leq N \\leq 10^91≤k≤N≤10
9
输出描述:
Output the number of headphones NIO should get.
示例1
输入
复制
3 1
输出
复制
4
说明
3 pairs of headphones = 6 headphones
4 headphones = 4 headphones
题意:
- 有N对耳机,妹妹准确地挑出了k对,问NIO要拿出多少只,才能保证拿到k+1对
思路:
- 最坏情况下NIO拿到的耳机全是单只的,因此需要拿(n-k)+(k+1)只,才能保证k+1对。
- 再判断下NIO要拿的个数是否已经超过剩下的耳机对数即可。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int main()
ios::sync_with_stdio(0), cin.tie(0),cout.tie(0);
LL n, k; cin>>n>>k;
if(n+1 > n*2-k*2)cout<<"-1\\n";
else cout<<(n-k)+(k+1)<<"\\n";
return 0;
B.Watches
链接:https://ac.nowcoder.com/acm/contest/33190/B
来源:牛客网
题目描述
NIO is the boss of the watch shop. One day, he wants to purchase a batch of watches from the manufactory. However, he lives in Amefica(not a real country), a country in is heavily taxed. If he buys kk watches, the i-thi−th watch in his list will cost him a_ia
i
(the original price) plus k \\times ik×i dollars (the i-thi−th one in the original list) . Now NIO only has MM dollars, so NIO asks you how many watches he can purchase actually.
输入描述:
There are multiple test cases.
For each test case, there are two lines. The first line contains two integers N, MN,M, denoting the number of watches he would like to buy and the amount of money NIO has, respectively. The second line contains NN integers, a_ia
i
represents that the price of the i-thi−th watch in the list.
1 \\leq N \\leq 10^5, 1 \\leq M \\leq 10^5, 1\\leq a_i \\leq 10^51≤N≤10
5
,1≤M≤10
5
,1≤a
i
≤10
5
输出描述:
Output a number, representing the maximum number of watches that NIO can purchase.
示例1
输入
复制
4 5
3 4 5 6
输出
复制
1
备注:
ii is starting from 11
题意:
- 给定n(1e5)件商品的价格,如果你选购k件商品,那么购买第i件物品的花费就是a_i+k*i,问最多能买多少件(第i件是原序列中的第i个)
思路:
- 注意到答案具有单调性,考虑二分答案k。
- 则问题变为判定是否能选择k件物品,总花费不超过M元,直接贪心即可
- check时对于k件物品算出所有物品的价值排个序从小到大尽可能的选。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL maxn = 2e5+10;
#define IOS ios::sync_with_stdio(0), cin.tie(0),cout.tie(0)
LL a[maxn], b[maxn];
LL n, m;
LL check(LL x)
for(LL i = 1; i <= n; i++)
b[i] = a[i]+i*x;
sort(b+1,b+n+1);
LL t = 0;
for(LL i = 1; i <= x; i++)
t += b[i];
return t<=m;
int main()
IOS;
while(cin>>n>>m)
for(LL i = 1; i <= n; i++)cin>>a[i];
LL l = 0, r = n+1, ans;
while(l < r)
LL mid = l+r+1>>1;
if(check(mid))l = mid;
else r = mid-1;
cout<<l<<"\\n";
return 0;
G.KFC Crazy Thursday
链接:https://ac.nowcoder.com/acm/contest/33190/G
来源:牛客网
题目描述
One day, NIO found an email on his computer from his friend Kala. He opened the email and found a picture with a large string of 26 lowercase letters. He asked Kala why he had sent him this picture. Kala said it was a challenge he had given to NIO: if NIO could figure out the number of palindromes end with ‘k’, ‘f’ and ‘c’ , he would buy NIO a KFC combo. The clever NIO turned on a AI software and converted all the letters on the image into a text file. NIO promised that he will share the KFC combo with you if you can help him.
输入描述:
There will be multiple test cases.
The first line a number NN, denoting the length of the string.
The second line is a string consists of lower letters ‘a’ to ‘z’.
1\\leq N\\leq 5\\times 10^51≤N≤5×10
5
输出描述:
A line with 33 numbers, denoting the number of palindromes, that end with ‘k’, ‘f’ and ‘c’.
示例1
输入
复制
6
kfccfk
输出
复制
3 3 3
说明
For the first ‘k’, 1 palindrome.
For the second ‘k’, 2 palindromes.
For the first ‘f’, 1 palindrome.
For the second ‘f’, 2 palindromes.
For the first ‘c’, 1 palindrome.
For the second ‘c’, 2 palindromes.
备注:
Palindromes with length greater or equal to one is considered. For example, ‘k’ is a palindrome.
题意:
- 求以kfc结尾的回文子串计数。
思路:
- 回文自动机模板题,初始化回文自动机之后,直接循环输入字符串统计回文子串的数量。
- 也可以马拉车O(n)统计一遍所有回文串,前缀和统计区间相应位置的kfc字母数量。
//题意:给出一个长为n的字符串,求它的最长回文子串长度
//思路:朴素做法为每次选定一个中心,向左右枚举判断回文串,复杂度O(n^2)。
//马拉车:在一个大的回文串内,[mid,r]与[l,r]是对称全等的,此时对于i属于[mid,r]且回文边界不超过大的回文串时,他的回文边界等价于p[2*mid-i],然后再对超过的部分重新暴力匹配,更新最靠右的大回文串。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e6+10;
char s[maxn], t[maxn<<1];
int p[maxn<<1],n;
int k[maxn],f[maxn],c[maxn];
long long ans[10];
int main()
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
while(scanf("%d", &n)!=EOF)
scanf("%s", s); int slen=strlen(s); t[0]='~'; t[1]='#';//~防止下标溢出
int i=0,j=1;
for(; i<slen; i++)t[++j]=s[i],t[++j]='#';//把可能的奇数偶数长度化为奇数求解,对称中心一定是#
t[j]='\\0';
int mid=0, r=0, tlen=strlen(t); //最大回文子串的中心和边界
for(int i=1; i<tlen; i++) p[i]=0;
for(int i=1; i<tlen; i++)
k[i]=k[i-1]+(t[i]=='k');
f[i]=f[i-1]+(t[i]=='f');
c[i]=c[i-1]+(t[i]=='c');
if(i<=r)p[i]=min(p[mid*2-i], r-i+1);//没有超过MX回文串边界时,可用对称性求解
while(t[i-p[i]]==t[i+p[i]])p[i]++;//超过边界时,暴力匹配
if(p[i]+i>r)r=p[i]+i-1, mid=i;//更新mid和r,保证r是最靠右的1
ans[0]=ans[1]=ans[2]=0;
//for(int i=1; i<tlen; i++) cout<<t[i]<<" ";cout<<'\\n';
//for(int i=1; i<tlen; i++) cout<<p[i]<<' ';cout<<'\\n';
for(int i=1; i<tlen; i++) //p[i]: 以i为中心的最长回文子串
if(t[i]=='#')
ans[0]+=(k[i+p[i]-1]-k[i-p[i]])/2;
ans[1]+=(f[i+p[i]-1]-f[i-p[i]])/2;
ans[2]+=(c[i+p[i]-1]-c[i-p[i]])/2;
else
ans[0]+=(k[i+p[i]-1]-k[i-p[i]]+1)/2;
ans[1]+=(f[i+p[i]-1]-f[i-p[i]]+1)/2;
ans[2]+=(c[i+p[i]-1]-c[i-p[i]]+1)/2;
cout<<ans[0]<<" "<<ans[1]<<" "<<ans[2]<<'\\n';
return 0;
H.Cutting Papers
链接:https://ac.nowcoder.com/acm/contest/33190/H
来源:牛客网
题目描述
NIO and his little four-year-old sister, Yasa, were doing the paper-cutting. NIO drew several line segments and get a close area, a polygon, from a mathematical inequality, |x|+|y|+|x+y| \\leq n∣x∣+∣y∣+∣x+y∣≤n. And Yasa drew a circle which center is coincide with the polygon’s center that NIO created, and the radius of the circle is half of nn.
They wanted to cut out union area of the polygon and the circle. Assume that they play the cutting game based on a infinite paper. What is the size of the area they cut from the paper?
输入描述:
There are multiple input cases.
Each case there are only one interger, nn.
1 < n \\leq 5\\times10^51<n≤5×10
5
输出描述:
Output a real number, representing the union area of the circle and the polygon. Float errors within 1e-6 would be considered as correct.
示例1
输入
复制
2022
输出
复制
3649785.912339927
说明
The inequality forms a polygon, and its center is the same with the circle. Output the size of union are of these two shapes.
题意:
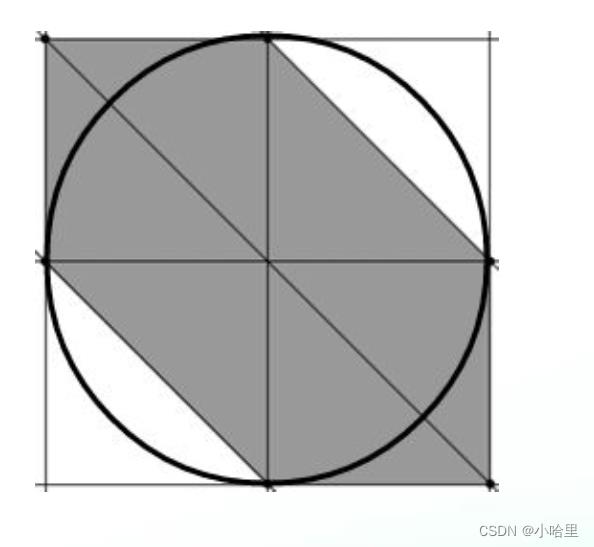
- 给出一个不等式,问这个不等式构成的封闭区域和以这个封闭区域中心为圆心的圆形的面积并。
思路:
- 根据不等式画出封闭区域,直接计算圆形和阴影部分的并集。
- 答案就是(n/2)^2*(2+pi/2)
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0), cin.tie(0),cout.tie(0)
typedef long long LL;
const double pi = acos(-1);
int main()
double n;
while(cin>>n)
double r = n/2, d = n*n/2;
double x = (pi*r*r+d*2)/2;
printf("%.10lf\\n", x);
return 0;
F.A Stack of CDs
链接:https://ac.nowcoder.com/acm/contest/33190/E
来源:牛客网
题目描述
NIO is playing a novel fraction game. The interface is shaped like an isosceles triangle of size NN. In each grid there is a fractional number. Every round, an isosceles triangle area of size kk is activated to click. And when the round is finished and a new round begins, a new area of a triangle is able to click, and the old area is locked, except the overlap region. For each triangle, NIO can click on a grid, and the fractional number inside this grid will be added to his score. If NIO clicks on a grid slowly, then he will get no score to add. If all possible triangles with size kk on the interface can be clicked during the game time. What is the maximum score NIO will get ideally? Size NN means that in the i-thi−th line there are ii triangles.
输入描述:
The are multiple test cases.
For each test case, the first line contains two numbers, NN denotes the height of the game interface and kk denoting the size of triangle that each round NIO can operate.
Following by NN lines, each line contains ii numbers. Each fractional number , a_ija
ij
is with the format of m/nm/n, represents the j-thj−th number in the i-thi−th line.
1 \\leq k \\leq N \\leq 10001≤k≤N≤1000, 1 \\leq m, n \\leq 10001≤m,n≤1000
输出描述:
Output the reduction of a fraction, representing the maximum score NIO will get. For example, “4/12” can be reduced to “1/3”.
示例1
输入
复制
3 3
1/3
5/28 11/37
14/31 17/29 7/47
输出
复制
17/29
备注:
The test data is guaranteed not to exceed long long during the operation. If the result is “3/1”, output “3/1” directly.
题意:
- 有一堆圆形,知道从底向上的顺序,上面的圆形会覆盖原来的圆形,问从上往下能看到的部分的周长
思路:
- 对于只有两个圆的时候,可以用余弦定理计算交点和圆形的连线和水平面的夹角。对每个圆
都搜索上面的所有这样的覆盖,计算每个盖住它的圆形的线段的左右端点,合并起来。最后计算没有被覆盖到的线段的长度。 - HAOI2008原题,下落的圆盘,洛谷P2510,改下多组数据和输入顺序即可。
//copy by dalao
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
const int maxn = 10005;
const double pi = 3.1415926535897932;
const double pi2 = 2*pi;
struct Point
double x, y;
;
inline double sqr(double x)
return x*x;
inline double get_dist(Point x, Point y)
return sqrt(sqr(x.x-y.x) + sqr(x.y-y.y));
struct Circle
Point O;
double r;
c[maxn];
inline double get_dist(Circle x, Circle y)
return get_dist(x.O, y.O);
int n;
struct Fugai
double l, r;
inline bool operator < (const Fugai& other) const
return l < other.l;
fugai[maxn];
int nown;
inline void cha(double l, double r)
fugai[++nown] = (Fugai)
l, r
;
bool gaif = false;//gaif = true表示该圆盘被上面的大圆盘完全覆盖
inline void jiao(Circle A, Circle B)
double dist = get_dist(A, B);
if(dist > A.r+B.r || A.r + dist < B.r)//没有任何覆盖
return;
if(dist + B.r < A.r)//如果被一个大圆盘完全覆盖,直接跳出
gaif = true;
return;
double alpha = acos((sqr(B.r)+sqr(dist)-sqr(A.r))/(B.r*dist*2.));//上图中的角CAD
double beta = atan2(B.O.y-A.O.y, A.O.x-B.O.x);//上图中的角CAE
double jiao1 = beta-alpha;//线段覆盖中的l
double jiao2 = beta+alpha;//线段覆盖中的r
if(jiao1 < 0 && jiao2 < 0)//对极角的一些特判
jiao1 += pi2, jiao2 += pi2;
if(jiao1 >= 0 && jiao2 <= pi2)
cha(jiao1, jiao2);
else
if(jiao1 < 0)
cha(jiao1+pi2, pi2);
cha(0, jiao2);
else
cha(jiao1, pi2);
cha(0, jiao2-pi2);
inline double get_ans()
double ans = 0;
sort(fugai+1, fugai+nown+1);
double lastr = fugai[1].l;
for(int i = 1; i <= nown; ++i)
if(lastr >= fugai[i].r)
continue;
if(fugai[i].l > lastr)
ans += fugai[i].r - fugai[i].l;
else
ans += fugai[i].r - lastr;
lastr = fugai[i].r;
return ans;
int main()
while(scanf("%d", &n) != EOF)
for(int i = 1; i <= n; ++i)
scanf("%lf%lf%lf", &c[i].O.x, &c[i].O.y,