Canvas 与 贝塞尔曲线（初步）

Posted 2021-04-29 前端深夜告解室

html5 技术发展至今，已经是前端工程师必备技能树之一了，而 Canvas 作为 HTML5 中重要的绘图工具，如今与 SVG 一起，共同撑起 web 可视化的天地。

Canvas 现在已经得到广大浏览器厂商的支持：

The canvas element is part of HTML5 and allows for dynamic, scriptable rendering of 2D shapes and bitmap images. It is a low level, procedural model that updates a bitmap and does not have a built-in scene graph.

这是摘自维基百科对 Canvas 的一句话介绍。简单来说，Canvas 就是用来绘制图形的。

Canvas 简单介绍

认识 Canvas

也许你没有用过 Canvas，这里有一篇官方教程足以让你用 Canvas 绘制一个简单的图形。如果你已经熟悉 Canvas，可以跳过这个章节，直接看下一章。

https://developer.mozilla.org/zh-CN/docs/Web/API/Canvas_API/Tutorial

简单来说，Canvas 就是一个 HTML 标签，通过 javascript 控制 Canvas 上下文，以达到绘制图形的目的。简单实例：

展现在浏览器中：

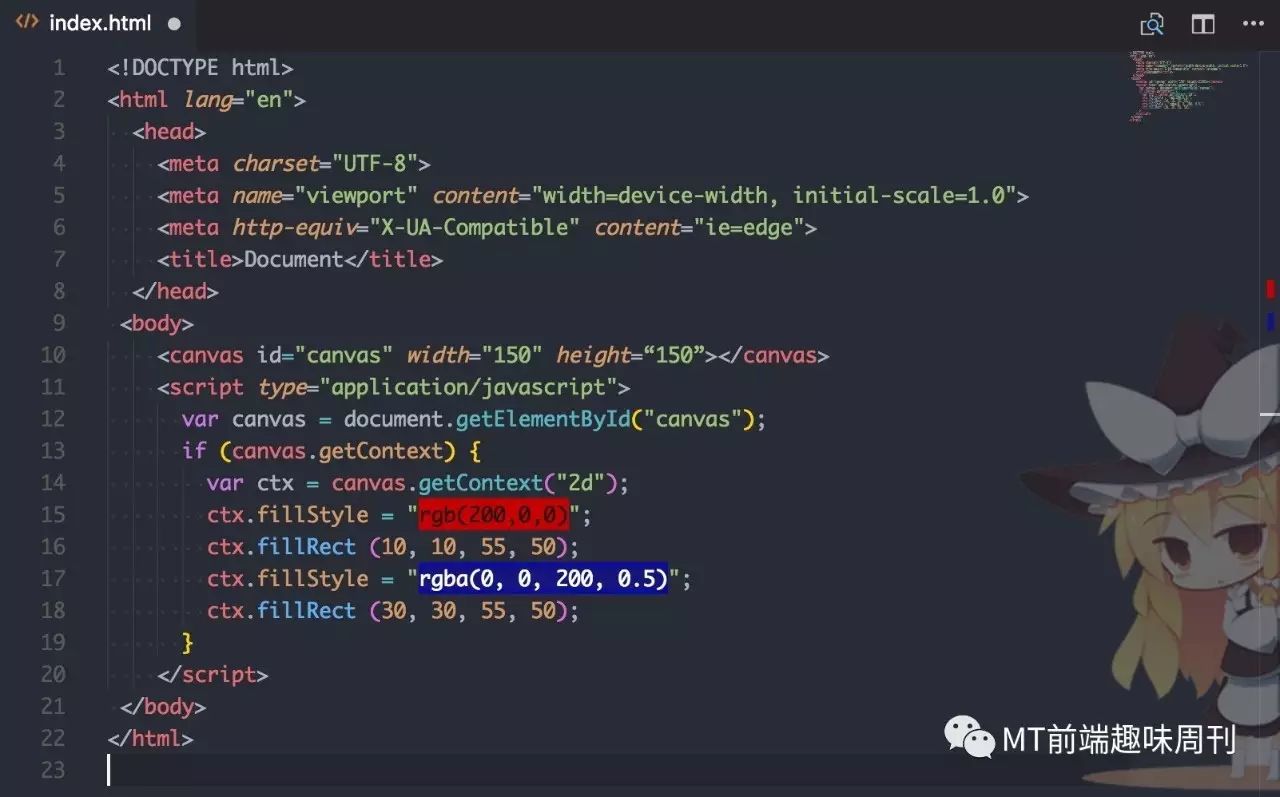
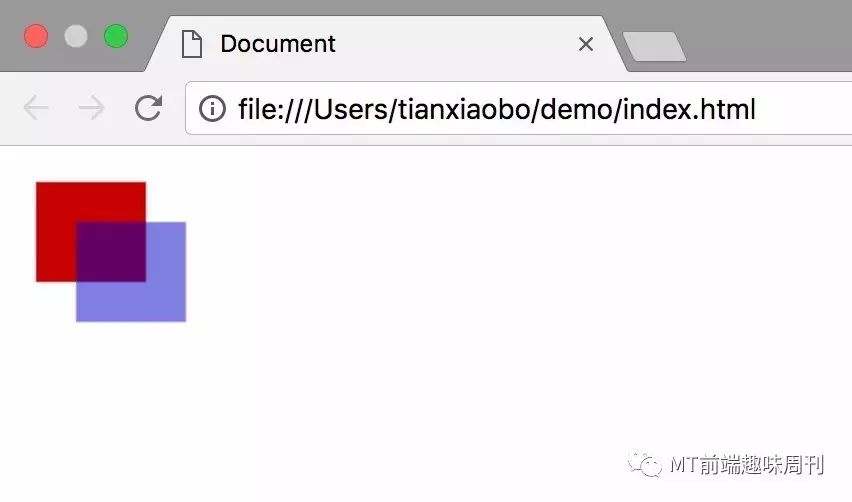
数据驱动渲染

正因为我们利用 JavaScript 来控制 Canvas 上下文来渲染图形，我们就很容易的利用数据来驱动 Canvas 的渲染。

这里自己写了一个非常简单的《别踩白块》小游戏，其原理就是利用数据的变动，来渲染 Canvas 画布更新。核心代码不到 100 行，我就放出来了：

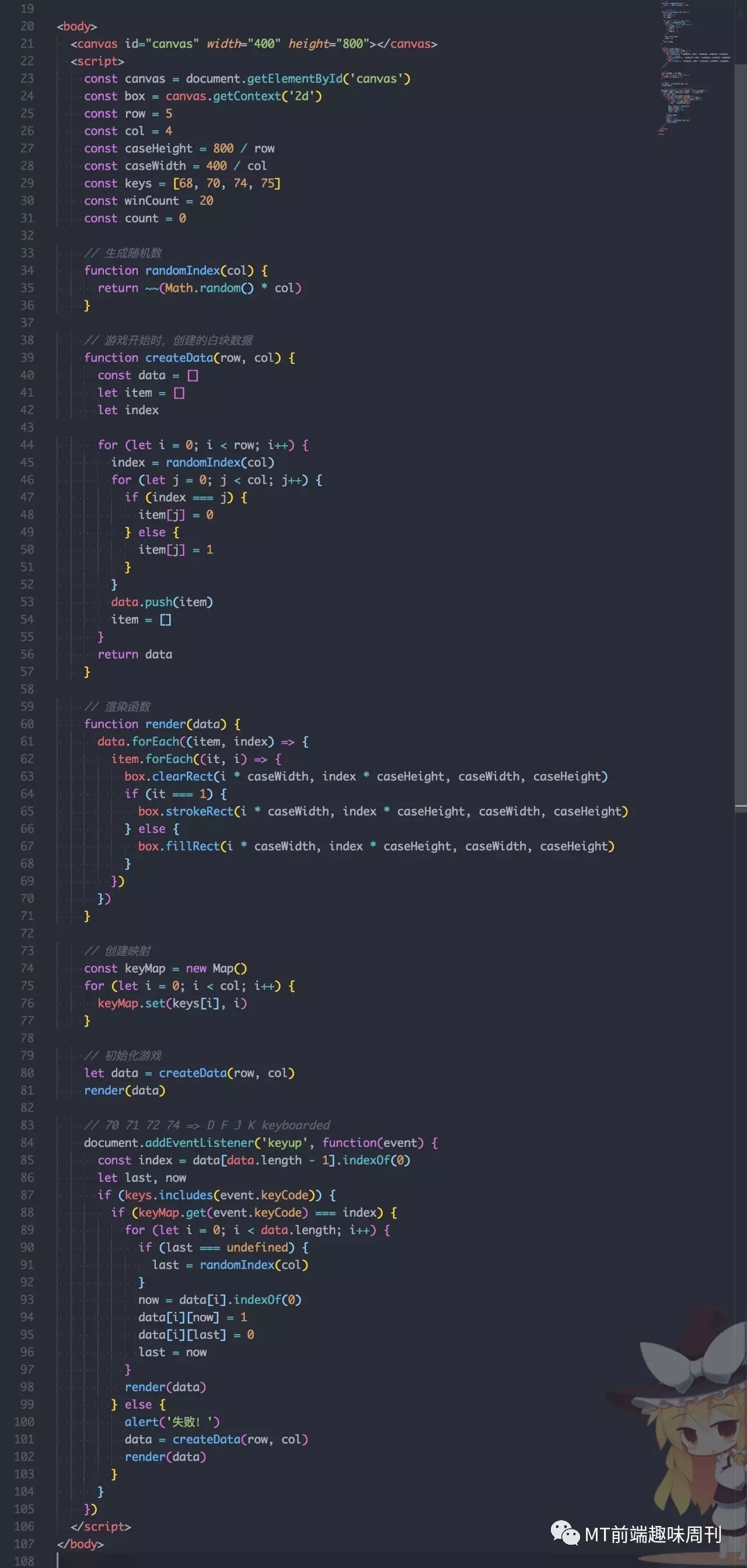
有兴趣的同学可以尝试利用 Canvas 写一些小游戏，非常适合用 Canvas 来进行渲染，比如 扫雷游戏。

Canvas 与 贝塞尔曲线

至此，我们对 Canvas 是一个怎样的元素有了一个较为清晰的认识，我们可以利用 Canvas API 来绘制基本形状了，但是这远不能满足我们对 Canvas 的探知，Canvas 绘制复杂图形的能力如何？

画图

画家利用手中的画笔，画出了很多不可思议的美景。Canvas 也提供了你这种能力。

A Bézier curve (pronounced [bezje]) is a parametric curve frequently used in computer graphics and related fields. Generalizations of Bézier curves to higher dimensions are called Bézier surfaces, of which the Bézier triangle is a special case.

In vector graphics, Bézier curves are used to model smooth curves that can be scaled indefinitely. "Paths", as they are commonly referred to in image manipulation programs,[note 1] are combinations of linked Bézier curves. Paths are not bound by the limits of rasterized images and are intuitive to modify.

以上摘自维基百科对 贝塞尔曲线的表述，看的出来，贝塞尔曲线对于绘制矢量图形的 Canvas 来说，简直是天作之合，而 Canvas 也提供了绘制贝塞尔曲线的接口，有了贝塞尔曲线，我们就可以绘制各种各样的图形了。

简单看一个 Canvas 的贝塞尔曲线实现的 DEMO：

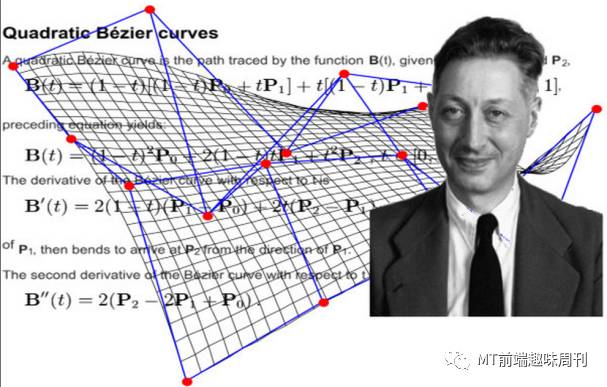
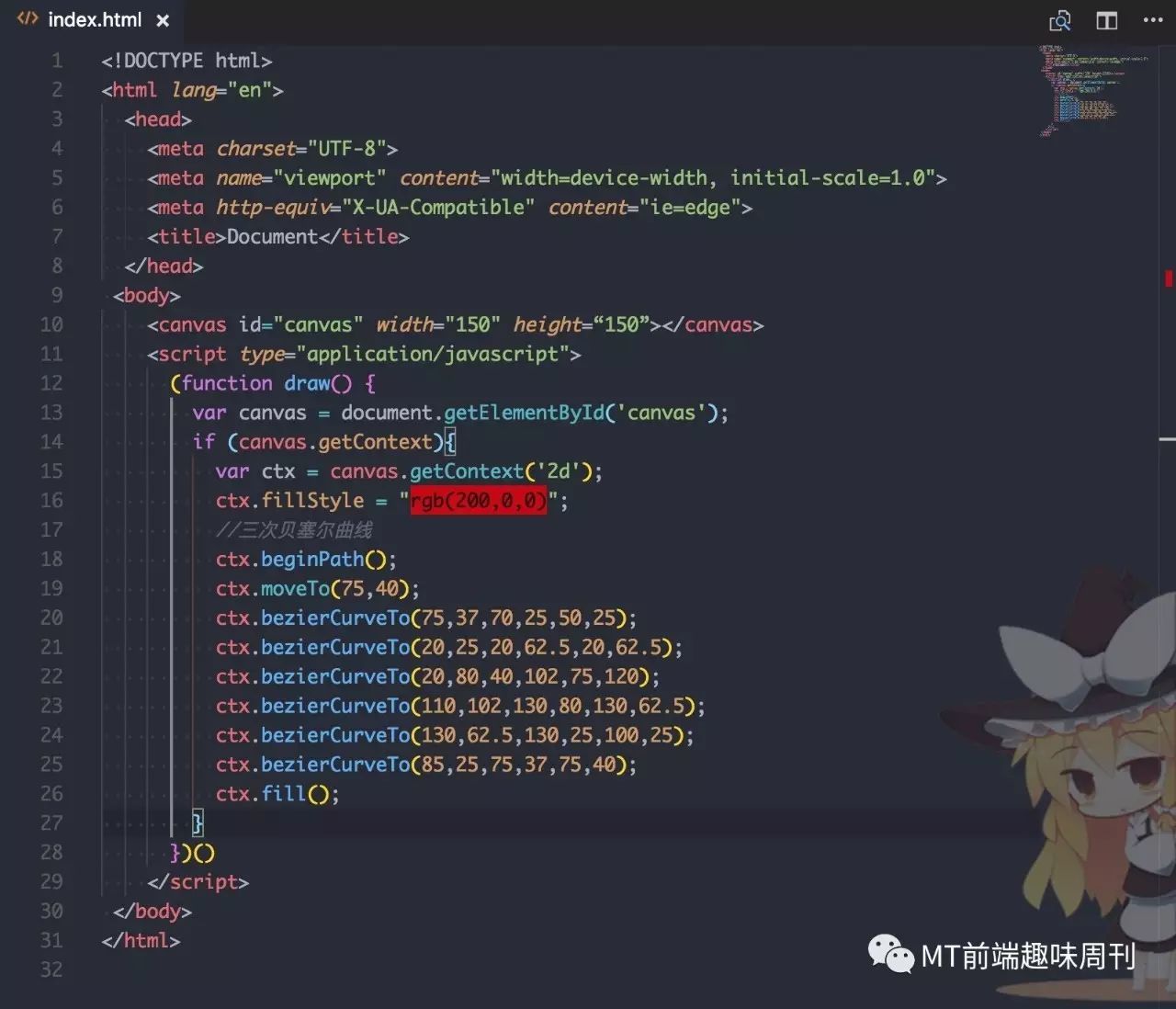
浏览器中：

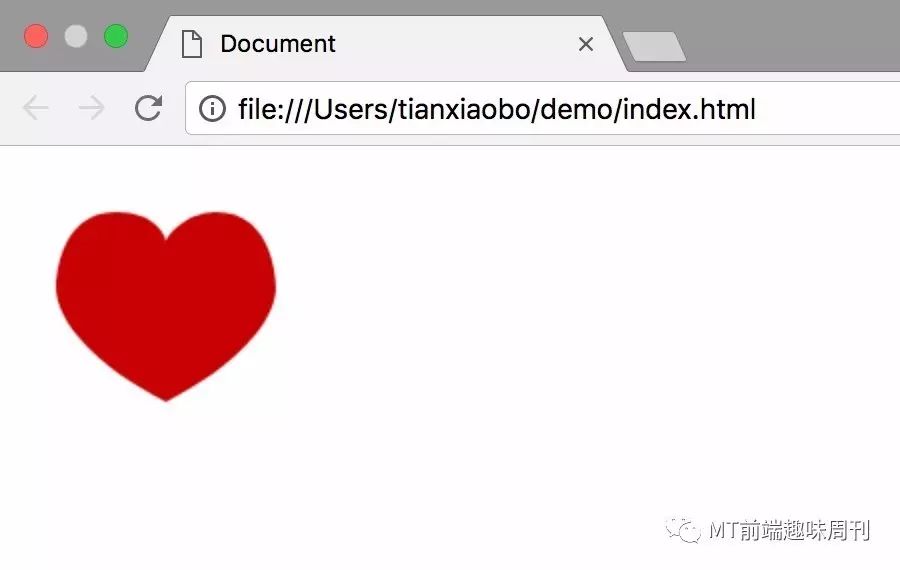
心这种不规则的曲线，就是贝塞尔曲线绘制出来的。

贝塞尔曲线通过“控制点”来绘制平滑曲线

看到上面的代码，很多没有接触过这个 API 的同学就会懵了，这一连串数字参数是什么？

其实就是在告诉 Canvas，绘制贝塞尔曲线所用的控制点。贝塞尔曲线就是利用这些控制点开绘制一条平滑的曲线。

其公式很简单（P1 就是控制点）：

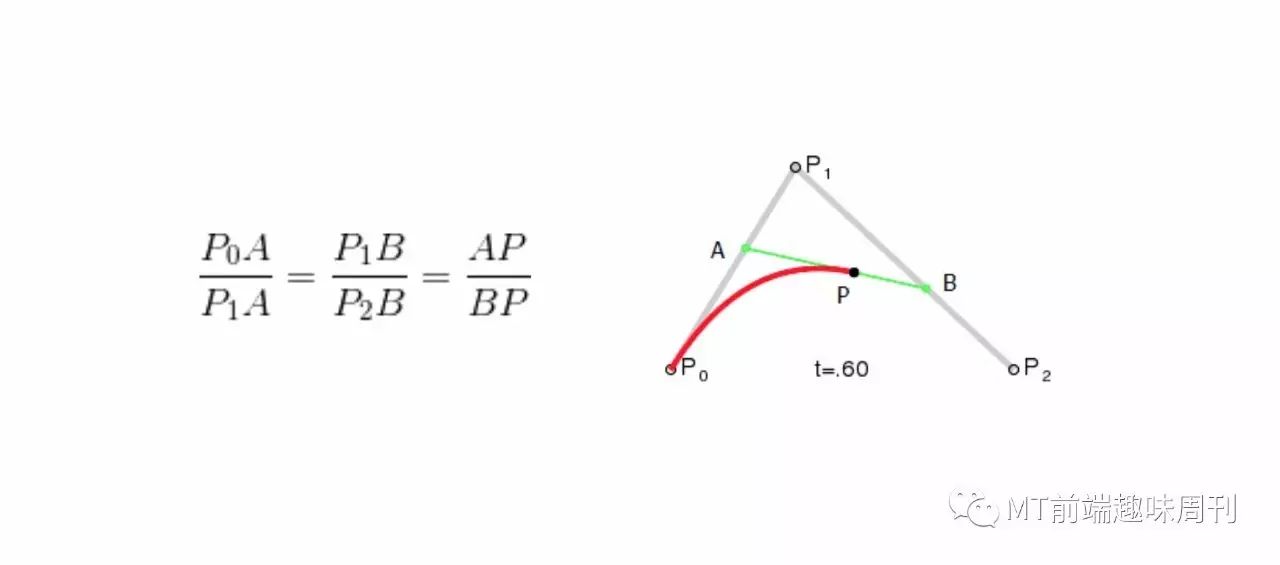
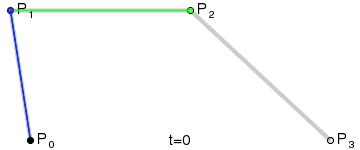
二次贝塞尔曲线

二次贝塞尔曲线，用过一个控制点，在首尾两点之间绘制一条曲线：

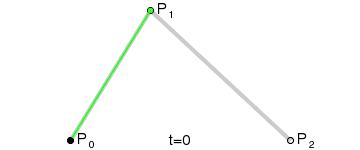
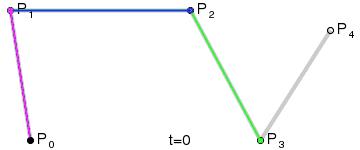
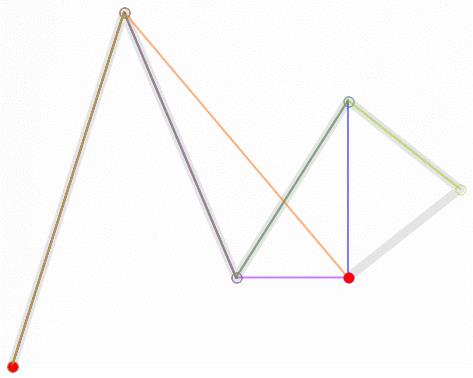
高阶贝塞尔曲线

所谓高阶，其实就是通过更多的控制点，在首尾两点之间绘制一条更为复杂的曲线：

除了 Canvas 中我们会用到 贝塞尔曲线 外，我们 CSS3 中常用的 transition属性，其缓动速率也是利用了贝塞尔曲线。

至此，我们就可以在 Canvas 中绘制任何我们想要的图形了。

结束了吗？

思考一个场景，我们需要绘制一张数据图表，这个数据的变化趋势是动态连续的。后端同学提供给前端的数据往往不会那么密集的（假设以一小时为单位，那么一天只有12个精准数据）。

很容易想到利用贝塞尔曲线平滑地穿过这些散点，可是细心的同学会发现，贝塞尔曲线是通过控制点来控制曲线，曲线并不穿过这些控制点。

那么如何找到这些控制点呢，使曲线可以平滑地穿过这些散点？有兴趣的同学可以研究研究，我将在下一篇 Canvas 与 贝塞尔曲线的文章中提供一种解决方案。

简历请投递至邮箱

[e-mail]

新美大智能支付终端团队

面向互联网开发从业者；

我们将分享团队技术文章，提供研发岗位招聘信息等。