非参数统计——Bootstrap方法

Posted 2021-04-29 We are Abel

最近事情真的太多了，我已经不想，也几乎没有时间再发推文了。但是鉴于距离评论功能的开启只差一个星期的推文，真香！

今天简单介绍一下Bootstrap估计区间的方法。

Bootstrap核心思想

Bootstrap核心思想容易理解，实际操作起来也很容易：

对原始数据重复抽样N次得到一系列“相同”统计量的值，对这些值计算标准差、分位数等来构造区间估计。

Bootstrap应用举例

数学期望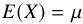的Bootstrap区间估计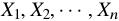，是一组独立同分布的样本，其数学期望的区间估计步骤：

(1)计算均值.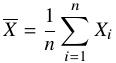

(2)在数据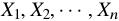中有放回抽取（无放回抽取也行）m个样本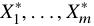，m为小于等于n且大于0的任意整数，计算均值.

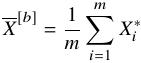(3)将第(2)步的过程重复进行B次，得到.

(4)找出新样本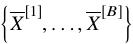的样本分位数

如：0.025样本分位数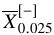，0.975样本分位数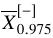，那么μ的95%置信区间为.

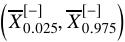基于正态近似的Bootstrap方法

(1)计算均值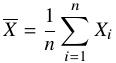

(2)在数据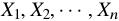中有放回抽取（无放回抽取也行）m个样本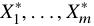，m为小于等于n且大于0的任意整数，计算均值.

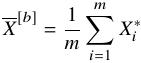(3)将第(2)步的过程重复进行B次，得到.

(4)有中心极限定理μ的95%近似置信区间为

.

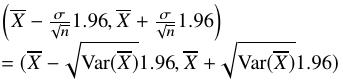(5)根据Bootstrap样本的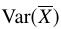估计为

.

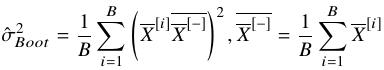基于正态近似的Bootstrap 95%置信区间为

.

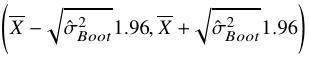这相当于利用Bootstr方法给出的估计.

Bootstrap方法的R实现

#################################################### 四： 标准正态分布均值的置信区间估计############
n=1000 ## 样本量x=rnorm(n) ## n个标准正态分布随机数t.test(x-0) ## 利用t检验 检验均值是否为0 可以给出基于t分布的95%置信区间
Norm.left=mean(x)-qnorm(0.975,0,1)/sqrt(n) ##基于标准正态分布的95%置信区间左端Norm.righ=mean(x)+qnorm(0.975,0,1)/sqrt(n) ##基于标准正态分布的95%置信区间左端
list(Norm.left,Norm.righ)
##################################################Boostrap方法
m=n/2 ## B=1000 ## bootstrap重复次数Exam1=0*seq(1,B,1) ## 设置1个B维的向量Exam2=Exam1
for(ii in 1:B){seed1=sample(1:n, m, replace=F) ## 在1：n序列里面“无放回”抽取m个正整数 ## "replace=F"表示无放回seed2=sample(1:n, m, replace=T) ## 在1：n序列里面“有放回”抽取m个正整数 ## "replace=T"表示有放回
x.boot1=x[seed1] ## 将seed1作为下标提取出原始数据的样本x.boot2=x[seed2] ## 将seed2作为下标提取出原始数据的样本Exam1[ii]=mean(x.boot1) ## 计算“无放回”的均值Exam2[ii]=mean(x.boot2) ## 计算“有放回”的均值
}
conf1=c(quantile(Exam1,0.025), quantile(Exam1,0.975)) ## “无放回”置信区间
conf2=c(quantile(Exam2,0.025), quantile(Exam2,0.975)) ## “有放回”置信区间
list(conf1=conf1, conf2=conf2)

########################################################### 基于正态近似和Bootstrap的置信区间### 标准差的Bootstrap估计
sd1=sqrt(var(Exam1)) ### 无放回sd2=sqrt(var(Exam2)) ### 有放回
Boot.left1=mean(x)-qnorm(0.975,0,1)*sd1 ##基于“无放回”的95%置信区间左端Boot.righ1=mean(x)+qnorm(0.975,0,1)*sd1 ##基于“无放回”的95%置信区间右端
Boot.left2=mean(x)-qnorm(0.975,0,1)*sd2 ##基于“有放回”的95%置信区间左端Boot.righ2=mean(x)+qnorm(0.975,0,1)*sd2 ##基于“有放回”的95%置信区间右端
list(Boot.left1,Boot.righ1) ## 无放回list(Boot.left2,Boot.righ2) ## 有放回

很快我就要写不下去了哈哈，因为实在是太忙了，如果大家有啥鼓励的话可以在后台留言~