深入浅出FM和类似推荐算法

Posted 2021-04-29 硅谷程序汪

硅谷程序汪

最近在实现Matrix Factorization的时候看到了Factorization Machine一系列算法，立刻被他和各种推荐模型的关联性吸引了，于是做了一些研究，总结一下。

前言

Factorization Machine (以下简称FM) 是由Steffen Rendle在2010年提出的，模型主要通过特征组合来解决大规模稀疏数据的分类问题。

这些年，由于深度学习的再一次兴起，人们将FM和深度学习产生特征联合到一起，在不同公司举办的CTR预估比赛中取得了非常好的成绩，表现尤为突出。2016年的LambdaFM和2017年的Field-aware FM则分别是推荐系统和CTR预估领域的经典做法。

什么是Factorization Machine

在面对CTR预估的问题的时候，我们常常会转化为下面这种类型的二分类问题，由于User，Country，以及内容等特征都是categorical类型，所以在使用的时候常常采用One-Hot Encoding将其转化为数值类型。

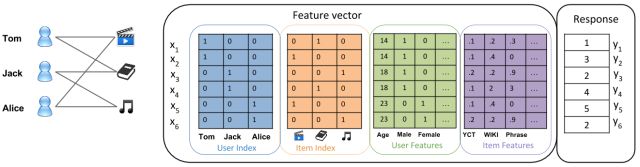
由上图可以看出，在经过One-Hot编码变换之后，每个样本的特征空间都变大了许多，特征矩阵变得非常稀疏，在现实生活中我们常常可以看见超过10^7维数的特征向量。

其次，如果我们采用单一的线性模型来学习用户的点击，打分习惯，我们很容易忽略特征中潜在的组合关系，比方说“男性用户”喜欢看“漫威电影”，买“奶粉”的用户也常常买“尿不湿”等等。为了学习这样的交叉特征，SVM率先引入了核的概念：

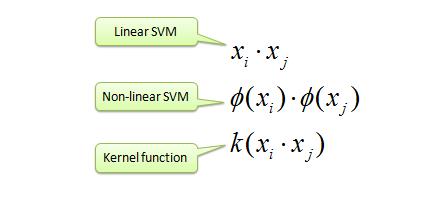
然而传统的SVM算法在面对稀疏特征的时候，对10^7维度数据生成了10^14参数，由于数据量有限，导致大部分参数学习失败。这时候FM就登场了，他通过对二阶参数加以限制，减少模型的自由度，分解为两个低秩矩阵乘积。

通过下面的这个表达试可以看出，FM很像是计算每一个经过One-Hot Encoding变化的特征的Embedding，然后学习不同特征之间Embedding相似度对于最后预测结果的影响。由于我们可以将上千万维的稀疏向量压缩为几十，或者几百维的Embedding，极大地减小了模型的参数数量级，从而增强模型的泛化能力，得到更好的预测结果。

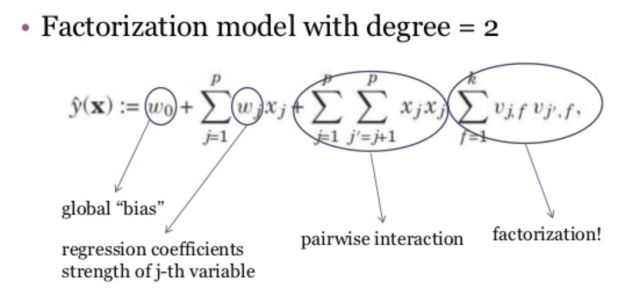
Field Factorization Machine

如果简单的考虑用户和推荐内容，我们可以把FM抽象成更简单的形式，通过学习整体平台的bias，每个用户的user bias，每个推荐内容的item bias，以及用户embedding和内容embedding的相似度权重，来优化平台的指标。

但是在实际预测过程中，推荐内容特征有不同的类别，就拿Pinterest来说，图片有图片的id，标题有标题的id，还有我们根据用户和图片交互过程计算的embedding。当我们想比较图片和标题相似度的时候，我们可以针对图片和标题分别计算隐向量，然后计算一个相似矩阵将他们转换到一起。我们也可以将图片id映射到多个隐向量上，生成图片对图片的embedding，图片对标题的embedding，图片对用户的embedding。

如果我们用下面的方程将不同的embedding根据他们的场组合起来，学习出不同场对排序权重的影响，就诞生了FFM。

在理论上，FM是一个单一场形式的FFM，在各大CTR预估比赛中，FFM都表现出了更好的结果。

FM与其他模型的关系

想到写FM相关文章的时候读到了Tracholar的文章《因子机深入解析》，受到了很大的启发，尤其是他对FM以及其他技术关联性的分析。经过授权，我将转载来自他文章中的关联分析，同时也附上原文链接：

https://tracholar.github.io/machine-learning/2017/03/10/factorization-machine.html

1. FM与矩阵分解

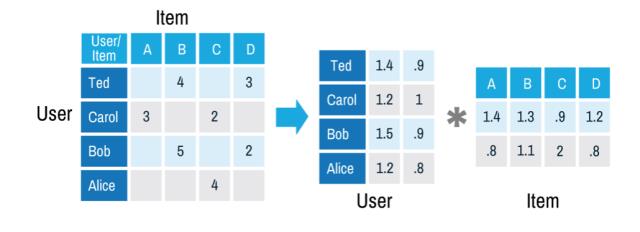
基于矩阵分解的协同过滤是推荐系统中常用的一种推荐方案[1]，从历史数据中收集user对item的评分，可以是显式的打分，也可以是用户的隐式反馈计算的得分。由于user和item数量非常多，有过打分的user和item对通常是十分稀少的，基于矩阵分解的协同过滤是来预测那些没有过行为的user对item的打分，实际上是一个评分预测问题。矩阵分解的方法假设user对item的打分R由User Embedding和Item Embedding相似性以及用户，物品的偏见决定。

这些参数可以通过最小化经验误差得到:

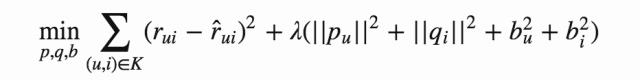
从上面的叙述来看，FM的二阶矩阵也用了矩阵分解的技巧，那么基于矩阵分解的协同过滤和FM是什么关系呢？以user对item评分预测问题为例，基于矩阵分解的协同过滤可以看做FM的一个特殊例子，对于每一个样本，FM可以看做特征只有userid和itemid的onehot编码后的向量连接而成的向量。从FM和MFCF公式来看，MFCF的用户embedding和item embedding可以看做FM中的隐向量，用户和item的bias向量就是FM中的一次项系数，常数μ也和FM中的常数w0相对应，可以看到，MFCF就是FM的一个特例！另外，FM可以采用更多的特征，学习更多的组合模式，这是单个矩阵分解的模型所做不到的！因此，FM比矩阵分解的方法更具普遍性！事实上，现在能用矩阵分解的方法做的方案都直接上FM了!

2. FM与决策树

FM和决策树都可以做特征组合，Facebook就用GBDT学习特征的自动组合[2]，决策树可以非常方便地对特征做高阶组合。如图所示，一棵决策的叶子节点实际上就对应一条特征规则，例如最左边的叶子节点就代表一条特征组合规则x1=1, x2=1。通过增加树的深度，可以很方便的学习到更高级的非线性组合模式。通过增加树的棵树，可以学习到很多这样的模式，论文[2]采用GBDT来建立决策树，使得新增的决策树能够拟合损失函数的残差。

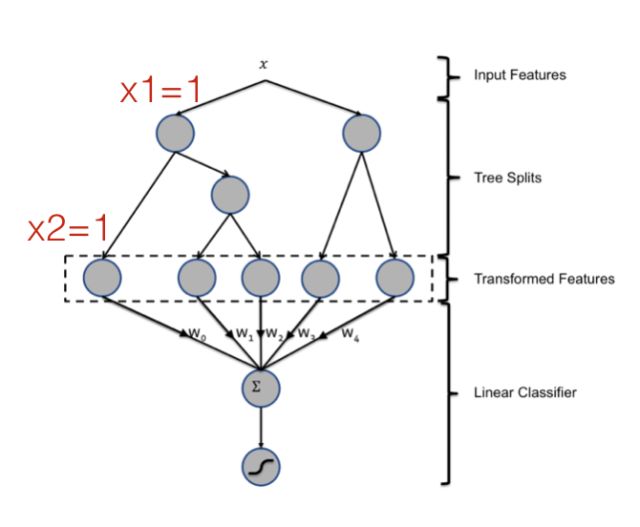
但是，决策树和二项式模型有一个共同的问题，那就是无法学习到数据中不存在的模式。例如，对于模式x1=1, x2=1，如果这种模式在数据中不存在，或者数量特别少，那么决策树在对特征x1分裂后，就不会再对x2分裂了。当数据不是高度稀疏的，特征间的组合模式基本上都能够找到足够的样本，那么决策树能够有效地学习到比较复杂的特征组合；但是在高度稀疏的数据中，二阶组合的数量就足以让绝大多数模式找不到样本，这使得决策树无法学到这些简单的二阶模式，更不用说更高阶的组合了。

3. FM与神经网络

神经网络天然地难以直接处理高维稀疏的离散特征，因为这将导致神经元的连接参数太多。但是低维嵌入(embedding)技巧可以解决这个问题，词的分布式表达就是一个很好的例子。事实上FM就可以看做对高维稀疏的离散特征做 embedding。上面举的例子其实也可以看做将每一个user和每一个item嵌入到一个低维连续的 embedding空间中，然后在这个embedding空间中比较用户和item的相似性来学习到用户对item的偏好。这跟 word2vec[3]词向量学习类似，word2vec将词embedding到一个低维连续空间，词的相似性通过两个词向量的相似性来度量。神经网络对稀疏离散特征做embedding后，可以做更复杂的非线性变换，具有比FM跟大的潜力学习到更深层的非线性关系！基于这个思想，2016年，Google提出wide and deep模型用作Google Play的app推荐[4]，它利用神经网络做离散特征和连续特征之间的交叉，神经网络的输出和人工组合较低维度的离散特征一起预测，并且采用端到端的学习，联合优化DNN和LR。如图所示，Catergorial 特征 embedding 到低维连续空间，并和连续特征拼接，构成了1200维的向量，作为神经网络的输入，神经网络采用三隐层结构，激活函数都是采用 ReLU，一起预测:

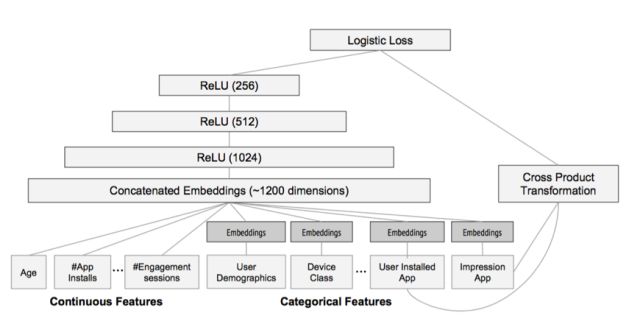
注意到，在 wide and deep 模型中，wide部分是通过对用户安装过的APP id和用户Impression App id做叉积变换，解决 embedding 的过泛化问题。 所谓的过泛化，实际上是因为用户的偏好本身就很集中，即使相似的一些 item，用户也只偏好其中一部分，使得query-item矩阵稀疏但是高秩。 而这些信息实际上已经反映在用户已有的行为当中了，因此可以利用这部分信息，单独建立wide部分，解决deep部分的过泛化。

从另一个角度来看，wide和deep部分分别在学习不同阶的特征交叉，deep部分学到高阶交叉，而wide部分学到的是二阶交叉。 后来，有人用FM替换了这里wide部分的二阶交叉，是得模型对高度稀疏的特征的建模更加有效，因为高度稀疏特征简单的叉积变换也难以有效地学到二阶交叉， 这在前面已经叙述过了。因此，很自然的想法就是，用FM替换这里的二阶交叉，得到DeepFM模型[5]。

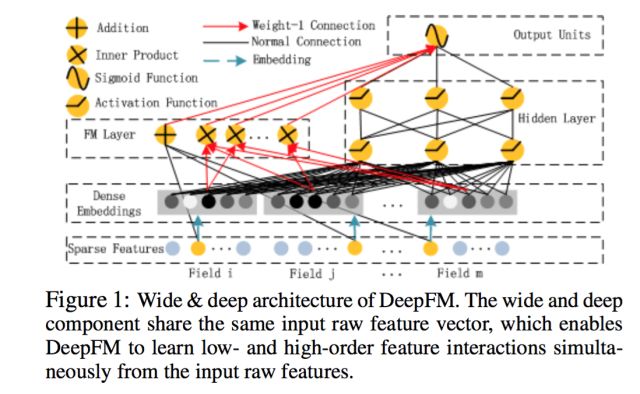
事实上，对于连续特征和非高度稀疏特征的高阶交叉，决策树似乎更加擅长。因此，很自然的想法是将GBDT也加到模型中。 但是问题是，决策树的优化方法和神经网络之类的不兼容，因此无法直接端到端学习。一种解决方案是，利用Boost融合的方案， 将神经网络、FM、LR当做一个模型，先训练一个初步模型，然后在残差方向上建立GBDT模型，实现融合。 微软的一篇文献[6]也证实，Boost方式融合DNN和GBDT方案相比其他融合方案更优，因此这也不失为一种可行的探索方向！

4. Cross Net

为了将FM推广到高阶组合，一系列的变体被研究人员提出，例如d-way FM, 高阶FM，但是应用到实际数据中的工作一直未见报道。 2017年，Google的研究人员从另一种思路触发，融合了残差网络的思想，设计出叉积网络Cross Net[7]，实现起来简单，可以通过加层的方式方便地扩展到任意阶数。具体来说，首先通过 embedding 层将稀疏特征转换成低维向量表示，将这些向量和连续值特征拼成一个大的d维向量，作为网络的输入。

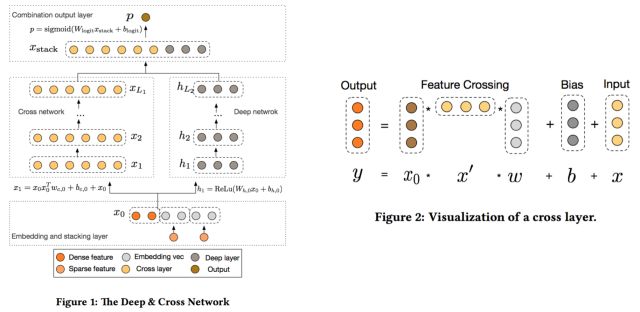
用x_l表示Cross net的的l层的输出，那么cross net的第l层的转换可以表示为

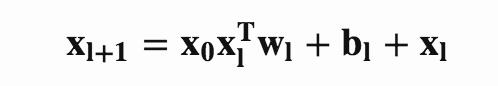
如果不考虑常数项和残差项，只保留第一项，并不断的递归会有

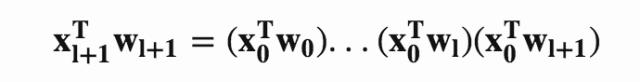
这表明，Cross Net可以看做FM的直接推广，FM是Cross Net的特例，当l=1且w0=w1时，就可以看做是FM！

We是embedding等效矩阵，x是原始稀疏高维特征向量！

原文: 因子机深入解析

https://tracholar.github.io/machine-learning/2017/03/10/factorization-machine.html

[1] Koren Y, Bell R M, Volinsky C, et al. Matrix Factorization Techniques for Recommender Systems[J]. IEEE Computer, 2009, 42(8): 30-37.

[2] He X, Pan J, Jin O, et al. Practical Lessons from Predicting Clicks on Ads at Facebook[C]. knowledge discovery and data mining, 2014: 1-9.

[3] Mikolov T, Sutskever I, Chen K, et al. Distributed representations of words and phrases and their compositionality[C]. neural information processing systems, 2013: 3111-3119.

[4] Cheng H T, Koc L, Harmsen J, et al. Wide & Deep Learning for Recommender Systems[C]// The Workshop on Deep Learning for Recommender Systems. ACM, 2016:7-10.

[5] Guo H, Tang R, Ye Y, et al. DeepFM: A Factorization-Machine based Neural Network for CTR Prediction[J]. arXiv preprint arXiv:1703.04247, 2017.

[6] Ling X, Deng W, Gu C, et al. Model Ensemble for Click Prediction in Bing Search Ads[C]//Proceedings of the 26th International Conference on World Wide Web Companion. International World Wide Web Conferences Steering Committee, 2017: 689-698.

[7] Wang R, Fu B, Fu G, et al. Deep & Cross Network for Ad Click Predictions[J]. arXiv preprint arXiv:1708.05123, 2017. MLA

欢迎关注硅谷程序汪