数据科学 | 第13讲：推荐算法

Posted 2021-04-29 狗熊会

如今信息呈现爆炸式增长，用户面对大量信息时往往无法从中获得对自己真正有用的信息，使得对信息的使用效率反而降低，这就是信息过载问题。推荐系统的出现就是为了解决上述的问题，它通过联系用户和用户的偏好信息（例如人们在浏览网站时，会留下一些评分、评论、点击等数据，这些数据往往可以反映出人们的偏好），一方面帮助用户发现对自己有价值的信息，另一方面让信息能够展现在对它感兴趣的人群中，从而实现信息提供商与用户的双赢。例如，在电子商务中，亚马逊、淘宝网等向用户推荐其可能将会购买的商品；在音乐服务中，网易云音乐等会向用户推荐其可能喜爱的音乐等等。

在这些推荐系统中，最为核心的就是推荐算法。所谓推荐算法，就是在推荐系统中，从用户的历史信息中挖掘用户偏好，进而预测用户可能喜欢的物品的算法。推荐算法种类繁多，有各自的优缺点和适合的应用场景，如基于内容的推荐算法、基于协同过滤的推荐算法、关联规则算法、基于知识的推荐算法等等。在这些推荐算法中，基于关联规则和基于协同过滤的推荐算法是最受人们关注且最常用的算法，本章将对这两种算法进行介绍。

关联规则

“尿布与啤酒”的故事是营销界的神话，一直为人们津津乐道。按常规思维，尿布与啤酒风马牛不相及，若不是借助数据挖掘技术对大量交易数据进行挖掘分析，沃尔玛是不会发现隐藏于其中的关联规律的。

数据关联是数据库中存在的一类重要的可被发现的知识。若两个或多个变量的取值之间存在某种规律性，就称为关联规则（association rules, AR）。关联规则可分为简单关联规则、时序关联规则、因果关联规则。关联规则分析的目的是找出数据库中隐藏的关联网。关联规则挖掘就是在事务数据库、关系数据库、交易数据库等信息载体中，发现存在于大量项目集合或者对象集合中有趣或有价值的关联或相关关系。

Agrawal等于1993年在分析购物篮问题时首先提出了关联规则挖掘，以后又经过诸多研究人员对其的研究和发展，到目前它已经成为数据挖掘领域最活跃的分支之一。关联规则的应用十分广泛，在购物篮分析（Market Basket Analysis），网络连接（Web Link Analysis）和基因分析等领域均有应用，具体应用场景包括优化货架商品摆放、交叉销售和捆绑销售、异常识别等。

1 基本概念

（一）项与项集

定义1 设 是m个不同项目的集合， （ ）称为数据项（Item），简称项；数据项集合I称为数据项集（Itemset），简称项集。I的任何非空子集X，若集合X中包含 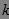个项，则称为 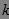项集（k-Itemset）。

项集其实就是不同属性取不同值的组合，不会存在相同属性、不同属性值的项集。例如，二项集{性别=男，性别=女}中两项是互斥的，现实中不会存在。

（二）事务与事务集

定义2 关联挖掘的事务集记为D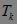， ， （ ）是项集I的非空子集，即 ，称为事务（Transaction）。每一个事务有且仅有一个标识符，称为TID（Transaction ID）。

（三）项集支持度与频繁项集

定义3 事务集D包含的事务数记为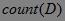 ，事务集D中包含项集X的事务数目称为项集X的支持数，记为 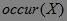，则项集X的支持度（Support）定义为：

                （13.1）

定义4 若 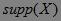大于等于预定义的最小支持度阈值，即  ，则称X为频繁项集，否则称X为非频繁项集。

一般情况下，给定最小支持数与给定最小支持度的效果是相同的，甚至给定最小支持数会更加直接且方便。加入需要寻找最小支持数为3的（频繁）项集，那么支持数小于3（0、1、2）的项集就不会被选择。

定理1 设X、Y是事务集D中的项集，假定 ，则：

（1） 

（2）Y是频繁项集 X是频繁项集

（3）X是非频繁项集 Y是非频繁项集

（四）关联规则

定义5  若 且 ，蕴含式 称为关联规则。其中项集X、Y分别为该规则的先导（antecedent或left-hand-side，LHS）和后继（consequent或right-hand-side，RHS）。

（五）关联规则支持度与置信度

定义6 项集 的支持度称为关联规则 的支持度，记作 ：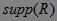

           （13.2）

定义7  关联规则 的置信度（Confidence）定义为：

             （13.3）

支持度描述了项集在事务集D中出现的概率的大小，是对关联规则重要性的衡量，支持度越大，关联规则越重要；而置信度则是测度关联规则正确率的高低。置信度高低与支持度大小之间不存在简单的指示性联系，有些关联规则的置信度虽然很高，但是支持度却很低，说明该关联规则的实用性很小，因此不那么重要。

从上述关于关联规则的定义可知，任意给出事务集D中两个项目集，它们之间必然存在关联规则，这样的关联规则将有无穷多种，为了在这无穷多种的关联规则中找出有价值规则，也为了避免额外的计算和I / O操作，一般给定两个阈值：最小支持度和最小支持度。

（六）最小支持度、最小置信度与提升度

定义8 关联规则必须满足的支持度的最小值称为最小支持度（Minimum Support）。

定义9 关联规则必须满足的置信度的最小值称为最小置信度（Minimum Confidence）。

如果满足最小支持度阈值和最小置信度阈值，则认为该关联规则是有趣的。支持度和置信度都不宜太低，如果支持度太低，说明规则在总体中占据的比例较低，缺乏价值；如果置信度太低，则很难从X关联到Y，同样不具有实用性。

最小支持度与最小置信度的给定需要有丰富的经验做参考，且带有很强的主观性，为此我们可以引入另外一个量，即提升度（Lift），以度量此规则是否可用。

定义10 对于规则 ，其提升度计算方式为：

         （13.4）

提升度显示了关联规则的左边和右边关联在一起的强度，提升度越高，关联规则越强。换而言之，提升度描述的是相对于不用规则，使用规则（效率、价值等）可以提高多少。有用的规则的提升度大于1。

（七）强规则与弱规则

定义11 若 且 ，或者 ，称关联规则 为强规则，否则称关联规则 为弱规则。关联挖掘的任务就是挖掘出事务集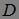中所有的强规则。

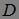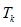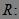例13.1 表13-1是某超市顾客购买记录的数据库 ，包含6个事务 （  ），其中项集 ={面包，牛奶，果酱，麦片}。考虑关联规则 {面包} {牛奶}。

表13-1 某超市顾客购物记录数据库D

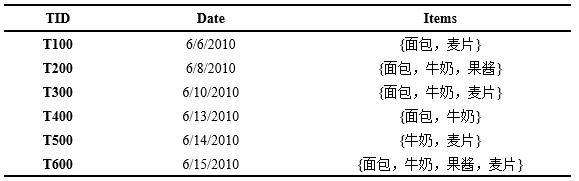
事务1、2、3、4、6中包含{面包}，事务2、3、4、6中包含{面包，牛奶}，支持度 ，置信度 ，若给定支持度阈值 ，置信度阈值 ，那么关联规则 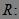{面包} {牛奶}是游泳的，即购买面包和购买牛奶之间存在强关联。计算提升度，知事务2、3、4、6中包含牛奶，则 ，意即对买了面包的顾客推荐牛奶，其购买概率是对随机顾客推荐牛奶的1.2倍，因此该规则是有价值的。

2 基本分类

关联规则可以根据以下标准进行若干分类。

（一）根据所处理变量的类型

关联规则可以分为布尔型关联规则（boolean association rules）和数值型关联规则（quantitative association rules）。布尔型关联规则处理的变量是离散的、分类的，它显示这些变量之间的关系；数值型关联规则可以处理数值型变量，将其进行动态分割，数值型关联规则中也可以包含种类变量。例如：

购买（“面包”）→购买（“牛奶”），考虑的是关联规则中数据项是否出现，即为布尔型关联规则；

年龄（“45-60”）→职称（“教授”），涉及的年龄是数值型变量，即为数值型关联规则，另外，此处一般都将数量离散化为区间。

（二）根据所涉及数据的维数

如果关联规则各项或属性只涉及一个维度，则它是单维关联规则（single-dimensional association rules）；而在多维关联规则（multidimensional association rules）中，要处理的数据将涉及多个维度。例如：

购买（“面包”）→购买（“牛奶”），这条规则只涉及顾客“购买”一个维度，即为单维关联规则；

年龄（“45-60”）→职称（“教授”），这条规则涉及“年龄”和“职称”两个维度，即为多维关联规则。

（三）根据所涉及的数据的抽象层次

关联规则可以分为单层关联规则（single-level association rules）和广义关联规则（generalized association rules）。在单层关联规则中，所有的数据项或属性只涉及同一个层次；而在广义关联规则中，将会充分考虑现实数据项或属性的多层次性。例如：

联想台式机→惠普打印机，是一个细节数据上的单层关联规则；

台式机→惠普打印机，是一个较高层次和细节层次之间的多层关联规则。

3 基本方法

有效建立规则的过程主要分为两个阶段，首先产生满足指定最小支持度的（频繁）项集，然后从每一个（频繁）项集中寻找满足指定最小置信度的规则。以下介绍最常用的两种算法。

（一）Apriori算法

Apriori 是一种挖掘产生0-1布尔型关联规则所需频繁项集的基本算法，也是目前最具影响力的关联规则挖掘算法之一。这种算法因利用了有关频繁项集性质的先验知识而得名，其核心是基于两阶段频集思想的递推算法，在分类上属于单维、单层、布尔型关联规则。

Apriori算法的基本思想是使用逐层搜索的迭代方法，用频繁的（k-1）-项集探索生成候选的频集k-项集（如果集合I不是频繁项集，那么包含I的更大的集合也不可能是频繁项集），再用数据库扫描和模式匹配计算候选集的支持度，最终得到有价值的关联规则。具体过程可用算法13.1描述。

算法13.1 Apriori算法

1. 发现频繁项集。

（1） 扫描事务数据库，计算每个项目出现的次数，根据预定义的最小支持度阈值 ，产生频繁1-项集 。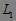

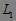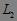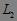（2） 用于找频繁 2-项集 ，而 用于找 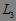，如此下去，直到不能找到满足条件的频繁 -项集，这时算法终止。这里在第 次循环中，过程先产生候选 -项集 ， 中的每一个项集是对 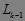中两个只有一个不同项的频集做一个（ -2）-连接来产生的。具体过程如下：

（2.1）   ，该函数由连接（join）步和剪枝（prune）步组成。join步对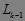 中每两个有（ -1）个共同项的频集进行连接，得到 ；prune步根据“频繁项集的所有非空子集都是频繁的”这一性质对 进行剪枝，得到 。

（2.2） 扫描数据库，确定每个事务 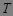所含候选集 的支持度 ，并存进hash表中。

（2.3） 去除候选集 中支持度小于 的项集，得到频繁k-项集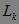 。中的项集是用来产生频集 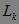的候选集，最后的频集 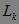必须是 的一个子集。

2. 由频繁项集产生关联规则。对于频繁项集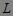 ，产生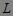 的所有非空子集 ，根据定理1知 也是频繁项集；对于每个非空子集 ，如果

则输出规则   。其中 和 分别是项集 和 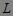在事务数据库 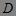中出现的频数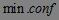， 是最小置信度阈值。由于规则由频繁项集产生，每个规则自然都满足最小支持度。

下面通过一个实例来说明应用Apriori算法挖掘一个事务数据库中频繁项集的过程。假设数据库 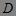中5个事务（见表13-2），支持度阈值60%（即最小支持度计数为3）。

表13-2 事务数据库D

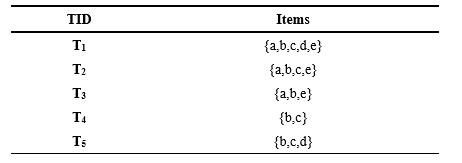
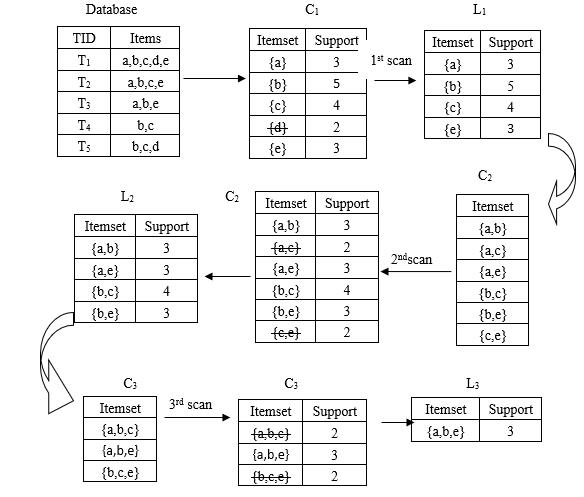
图13-1 Apriori算法的一个实例

如上图13-1所示，第一次扫描数据库，得到候选1-项集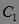 及其各项的出现频数，删除 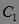中出现频数小于2的项，得到频繁1-项集 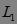。然后，使用 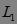生成候选2-项集 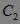，第二次扫描数据库，得到 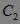各项的出现频数，删除 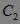中出现频数小于2的项，得到频繁2-项集 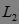。最后，使用 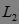并根据Apriori性质剪枝，生成候选3-项集 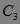，第三次扫描数据库，得到 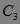各项的出现频数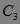（ 中没有出现频数小于2的项），得到频繁3-项集 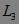。 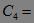Ø，算法终止，所有的频繁项集均被找出。

接着，针对最后的频繁项集L3={a,b,e}，其非空子集有{a}、{b}、{e}、{a,b}、{a,e}和{b,e}，产生关联规则如下：

{a} {b,e}， Confidence=3/3=100%

{b} {a,e}， Confidence=3/5=60%

{e} {a,b}， Confidence=3/3=100%

{a,b} {e}， Confidence=3/3=100%

{a,e} {b}， Confidence=3/3=100%

{b,e} {a}， Confidence=3/3=100%

若最小置信度阈值为80%，则仅有第二条规则无法输出。

从以上算法的运行过程，我们可以看出Apriori算法的优点：简单、易理解、数据要求低。但是，这个方法搜索每个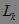 需要扫描一次数据库，即如果最长模式为n，那么就需要扫描数据库n遍，这无疑需要很大的I / O负载。因此，可能需要重复扫描数据库，以及可能产生大量的候选集，是Apriori算法的两大缺点。

R语言实现

关联规则

关联规则可以被用在购物篮分析等一些常规场合，它的主要目的就是从已有的大量数据资料中挖掘出可被利用的、有价值的规则信息，然后将其应用到现实中以获取更多效益。我们首先介绍R语言中实现关联规则的函数。

在R语言中，可以使用arules包中的apriori()函数来实现关联规则挖掘。函数的基本形式为：

apriori ( data , parameter = list ( slots ),appearance = list ( slots ) , control = list ( slots ) )

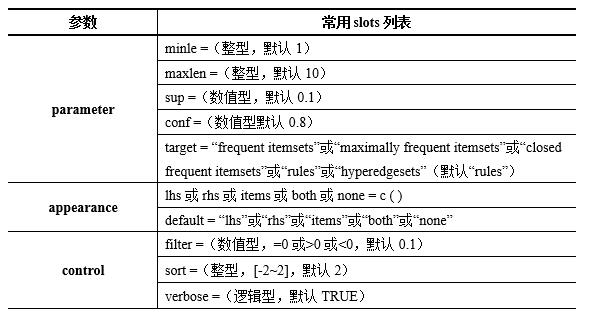
其中data是输入交易数据或者类交易数据，比如二进制矩阵或者数据框。parameter、appearance、和control参数均是命名列表，内部均定义有多个slots，具体见表13-3。

表13-3 定义在参数parameter、appearance、和control中常用slots

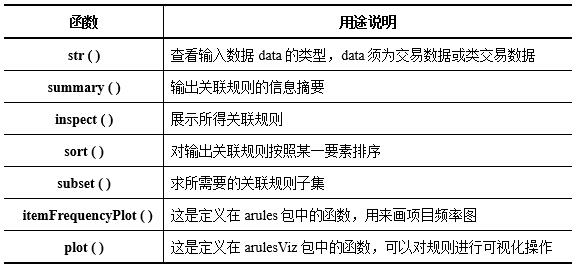
在进行关联分析时与apriori()连用的函数主要有str()、summary()、inspect()、sort()、subset()、 itemFrequencyPlot()和plot()等，具体用途说明见表13-4。

表13-4与apriori(.)连用的常用函数

接着就通过一个案例来说明关联规则在R语言中具体实现。我们的案例所用的数据集选自IBM SPSS Modeler自带的案例数据：BASKETS1n（某超市1000名顾客的购买记录）。变量包括顾客ID，性别、是否是本地人、年龄、收入等个人信息，也包括购买产品，如是否购买果蔬、鲜肉、乳制品、啤酒、鱼等以及购买金额和购买方法。现在超市希望能找出顾客购买产品之间的关系，即是否购买了A产品的顾客，也购买了B产品。

（一）数据读入

先把原始数据转化为".csv"格式，然后将其保存在R当前工作目录中。以下为分析过程及结果。

> baskets0 <- read.csv ( "BASKETS1n.csv" ) # 读取数据
> dim ( baskets0 )
[1] 1000   18
> colnames ( baskets0 )
 [1] "cardid"        "value"         "pmethod"       "sex"          
 [5] "homeown"       "income"        "age"           "fruitveg"     
 [9] "freshmeat"     "dairy"         "cannedveg"     "cannedmeat"   
[13] "frozenmeal"    "beer"          "wine"          "softdrink"    
[17] "fish"          "confectionery"
> summary ( baskets0 )
# 篇幅限制，此处没有列出结果

原始数据库集共有1000组观测值，每组观测值包含18个变量信息。根据研究性质，这18个变量中“cardid”、“value”、“pmethod”等前7个变量是分析所不需要的，应剔除。

> baskets <- baskets0 [ , -1 : -7 ] # 剔除无关变量
> str ( baskets )
'data.frame':    1000 obs. of  11 variables:
 $ fruitveg     : logi  FALSE FALSE FALSE FALSE FALSE FALSE ...
 $ freshmeat    : logi  TRUE TRUE FALSE FALSE FALSE TRUE ...
 $ dairy        : logi  TRUE FALSE FALSE TRUE FALSE FALSE ...
#篇幅限制，省略部分结果

剔除了“cardid”、“value”、“pmethod”等前7个无关变量，剩下的11个变量均为逻辑型，适用于做关联分析。

（二）关联分析

在R中，关联分析使用arules包中的apriori()函数实现。

> install.packages ( "arules" ) # 装载"arules"包
> library ( arules )

在准备工作做好以后，先来利用arules包中的itemFrequencyPlot()函数做一张频率图。

> trans <- as ( baskets , "transactions" )  # 这里做转换是为方便作图需要
> windows ( 6 , 4 )
> itemFrequencyPlot ( trans , sup = 0.1 , topN = 11 , col = grey.colors ( 11 ) )

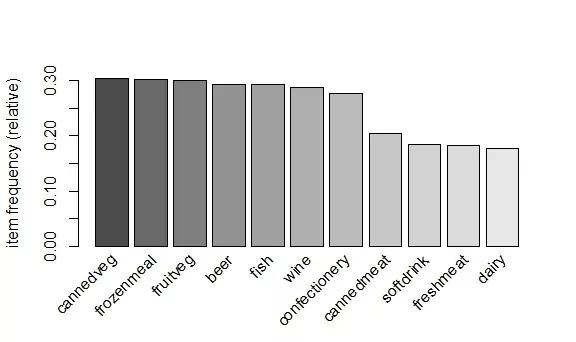
图13-2 食物出现频率

从频率图13-2中可以很明显看出，罐装蔬菜出现频率最高，超过0.3，即这1000位顾客中有300多人买了罐装蔬菜，接下来依次是冻肉、果蔬、啤酒和鱼等食物，相比较而言，购买乳制品的顾客最少。

> rules1 <- apriori ( baskets , control = list ( verbose = FALSE ) )
> summary ( rules1 )
set of 3 rules
rule length distribution (lhs + rhs):sizes
3 
3 
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
      3       3       3       3       3       3 
summary of quality measures:
    support        confidence          lift      
 Min.   :0.146   Min.   :0.8439   Min.   :2.834  
 1st Qu. :0.146   1st Qu.:0.8514   1st Qu.:2.857  
 Median :0.146   Median :0.8588   Median :2.880  
 Mean   :0.146   Mean   :0.8590   Mean   :2.870  
 3rd Qu. :0.146   3rd Qu.:0.8665   3rd Qu.:2.888  
 Max.   :0.146   Max.   :0.8743   Max.   :2.895  
mining info:
    data ntransactions support confidence
 baskets          1000     0.1        0.8
> inspect ( rules1 )
    lhs                     rhs         support  confidence   lift    
[1] {frozenmeal,beer}      => {cannedveg}  0.146   0.8588235  2.834401
[2] {cannedveg,beer}       => {frozenmeal} 0.146   0.8742515  2.894873
[3] {cannedveg,frozenmeal}  => {beer}       0.146   0.8439306  2.880309

在默认条件下（support = 0.1, confidence = 0.8），仅挖掘出3条规则。结合灌装蔬菜出现频率最高仅有0.3多一点的情况，这些规则的支持度（均超过0.14）已经相当高，另外它们的置信度均大于0.84，提升度也都超过了2。但是，仔细观察可以发现，这三条规则事实上仅是同一条规则的变相而已。因此，接下来我们将调整相关参数以挖掘更多规则。

> rules2 <- apriori ( baskets, parameter = list ( supp = 0.03 , conf = 0.8 , target = "rules" ) , 
                control = list ( verbose = FALSE ) )
> summary ( rules2 )
set of 15 rules
rule length distribution (lhs + rhs):sizes
 3  4 
 3 12 
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
    3.0     4.0     4.0     3.8     4.0     4.0 
summary of quality measures:
    support         confidence          lift      
 Min.   :0.0360   Min.   :0.8182   Min.   :2.709  
 1st Qu.:0.0360   1st Qu.:0.8475   1st Qu.:2.822  
 Median :0.0400   Median :0.8627   Median :2.895  
 Mean   :0.0604   Mean   :0.8636   Mean   :2.886  
 3rd Qu.:0.0440   3rd Qu.:0.8790   3rd Qu.:2.935  
 Max.   :0.1460   Max.   :0.9167   Max.   :3.035  
mining info:
    data ntransactions support confidence
 baskets          1000    0.03        0.8
> rules2.sorted <- sort ( rules2 , by = "lift" ) # 参照“lift”大小对规则（默认为降序）排列
> inspect ( rules2.sorted [ 1 : 5 ] ) # 展示排序后的前五条规则
    lhs                             rhs         support  confidence  lift    
[1] {cannedveg,beer,fish}           => {frozenmeal}  0.044   0.9166667  3.035320
[2] {fruitveg,cannedveg,frozenmeal}  => {beer}        0.040   0.8888889  3.033750
[3] {cannedmeat,frozenmeal,beer}    => {cannedveg}  0.036   0.9000000  2.970297
[4] {cannedveg,frozenmeal,fish}     => {beer}       0.044   0.8627451  2.944523
[5] {cannedveg,frozenmeal,wine}    => {beer}       0.036   0.8571429  2.925402

调整阈值（降低最小支持度）后，挖掘到15条规则，提升度也全都超过2.5，属于强有用规则。下面我们利用arulesViz包中的作图函数来对这些规则进行可视化操作。

> library ( arulesViz ) # 简单可视化
> windows ( 6 , 4 )
> plot ( rules2 )

从图13-3中可以看出，这15条规则的置信度均高于0.8，其提升度也全都超过2.5，但是绝大多数规则的支持度仅在0.04左右，并且随着提升度的增加，其支持度和置信度并未相应提高。

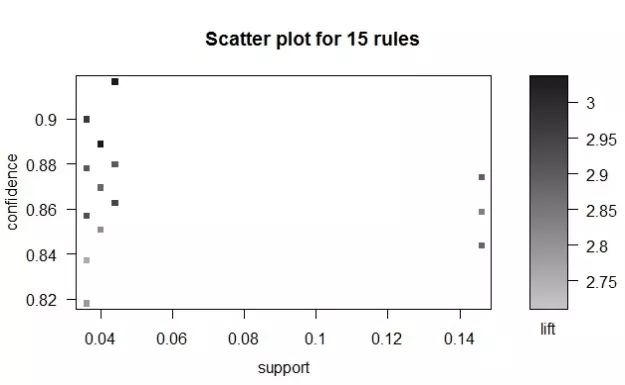
图13-3 简单可视化

在这15条规则中仍然包含冗余规则，继续筛选。

# 删除冗余的规则
> subset.matrix <- is.subset ( rules2.sorted , rules2.sorted )
> subset.matrix [ lower.tri ( subset.matrix , diag = T ) ] <- NA
> redundant <- colSums ( subset.matrix , na.rm = T ) >= 1
> which ( redundant )
 [1]  4  6  7  9 10 11 12 13 14 15
> rules2.pruned <- rules2.sorted [ ! redundant ]
> inspect ( rules2.pruned )
  lhs                               rhs          support  confidence     lift
1 {cannedveg,  beer, fish}          => {frozenmeal}   0.044   0.9166667  3.035320
2 {fruitveg, cannedveg, frozenmeal}   => {beer}        0.040   0.8888889  3.033750
3 {cannedmeat, frozenmeal, beer}     => {cannedveg}    0.036   0.9000000  2.970297
4 {cannedveg, frozenmeal, wine}      => {beer}         0.036  0.8571429  2.925402
5 {cannedveg, beer}                => {frozenmeal}   0.146   0.8742515  2.894873 

第4、6、7、9、10、11、12、13、14、15条是冗余规则，删去，最终得到5条有价值的关联规则。

（三）结果分析

解析最后得到的五条规则，可以得出以下结论：

（1）有91.66%的置信度保证购买罐装蔬菜、啤酒、鱼的顾客会继续购买冻肉；

（2）在保证可信度不低于0.8的条件下，购买罐装蔬菜和啤酒的顾客继续购买冻肉的可能性最大；

（3）灌装蔬菜与冻肉、灌装蔬菜与啤酒、冻肉与啤酒之间均存在双向关联。

因此，对于超市而言，可以在蔬菜、海鲜区放置啤酒专柜以促进啤酒的销售；可以将灌装蔬菜与冻肉、灌装蔬菜与啤酒、冻肉与啤酒等进行捆绑销售以增加这些商品销量。

最后再说明两点，首先，apriori是一个非常强大的算法，在你对数据还不太了解的时候，它可以为你提供一个了解数据的有趣的视角；其次，尽管最终的规则是在这份数据集基础上，系统性生成的，但是设定阈值真心是一门艺术，这取决于你想要得到什么样的规则，你可能需要一些能够帮助你做出决策的规则，另外这些规则也可能会将你引入歧途。

协同过滤等更多推荐算法请见《数据科学》一书！

协同过滤等更多推荐算法更多推荐算法请见《数据科学》一书！

注：由于微信排版限制，部分公式未对齐，书籍中均正常。

▼

往期精彩回顾

▼

作者简介

方匡南，厦门大学经济学院教授、博士生导师、耶鲁大学博士后、厦门大学数据挖掘研究中心副主任。入选国家“万人计划”青年拔尖人才，国际统计学会推选会士（ISI Elected member），全国工业统计学会常务理事、数据科学与商业智能学会常务理事，中国青年统计学家协会常务理事等。主要研究方向为 数据科学，机器学习，应用统计。先后与华为、华星光电、厦门国际银行、南方电网、普益标准、北京诺信创联等众多企业有联合研究，先后为联通、华星光电、建设银行、农业银行、国元集团等众多企业提供培训。

欢迎选购作者新作《数据科学》

了解更多详情

﹏

﹏

﹏

﹏

京东自营

当当自营