论文笔记之Neural Collaborative Filtering

Posted 2023-03-17

参考技术A 文中指出虽然之前有一些工作使用deep learning来解决推荐问题，但这些工作基本上使用deep learning来对辅助信息建模，对于协同过滤的关键信息——user和item的交互信息，之前的工作仍然使用矩阵分解(MF)，将users和items映射到一个共享的隐空间，然后对users和items的latent feature做内积。
用神经网络结构代替内积操作，可以从数据中学到任意函数，基于此本文提出了NCF模型(Neural network-based Collavorative Filtering)。本文专注于利用隐反馈信息(implicit feedback, 如浏览、点击等行为;explicit feedback指评分、评论等行为)。

有M个users, N个items。user-item交互矩阵Y(M * N维，反应了用户的隐反馈信息)定义为，

yu,i = 1只能说明用户u和物品i有交互，并不能说明用户u喜欢物品i；同样的，yu,i = 0不能说明用户u不喜欢物品i。
在这种情况下，观察到的数据至少能从一定程度上反应用户的兴趣，而未观察到的数据只能视为missing data，这就导致了负反馈的缺乏。
隐反馈推荐问题就是要估计Y中未观测物品的score，然后以此来对物品排序。(再次强调，这种应用场景下，对于以点击或浏览的物品是不知道用户是否喜欢的)
问题可以描述为学习下式，

y^u,i为交互yu,i的预测score，Θ为模型参数，f为映射函数。
文中提到优化目标参数，一般有两种目标函数：pointwise loss和pairwise loss。pointwise loss通常用于回归框架，最小化y^u,i和yu,i的squared loss。对于缺乏negative data问题，将所有的未观测数据视为负反馈，或者从未观测数据中采样negative instances。
pairwise learning中，观测到的数据应该排在未观测数据的前面，因此最大化y^u,i和yu,i的边界。
NCF支持pointwise和pairwise learning两者。

pu表示用户u的latent vector，qi表示物品i的latent vector，MF使用pu和qi的内积来估计y^u，

K表示latent space的维度。MF可以看作是latent factor的线性模型。

上图说明了MF的局限性。对于user-item矩阵(a)，u4与u1最相似，接下来是u3，最后才是u2。而在latent space (b)中，使p4更靠近p1会使p4更靠近p2而不是p3，这会增大ranking loss。

可以增大K来解决这个问题，但会降低模型的泛化能力，可能导致过拟合。
本文使用深度神经网络来学习这种交互关系。

最底下的input layer包括两个特征向量，分别描述用户u和物品i，它们可以根据具体问题具体定制。在本文中，用户u和物品i的one-hot作为输入。
上面是embedding layer，采用全连接，将稀疏的input映射成稠密的embedding(user和item的embedding都是k维)。
user和item的embedding向上进入全连接的神经网络结构，称为neural collaborative filtering layers，将latent vector映射成预测的score。(对于不同的问题，这里的每一层layer也是可以定制的)
layer X的维度决定了模型的capability。
通过最小化y^u,i和yu,i的pointwise loss来训练模型。(文中提到另一种训练模型的方法，使用pairwise learning，比如使用Bayesian Personalized Ranking和margin-based loss，但文中后面部分使用的是pointwise loss)
整个预测模型可以表示为，

P(M * K维)和Q(N * K维)分别表示users和items的latent factor matrix，Θf为模型参数。
f被定义为一个多层神经网络，因此可以表示为，

φout表示输出层映射，φx表示第x层的映射，共X层。

大多数的pointwise方法将损失函数定义为，

y表示Y中观测到的交互关系集合，y-表示负样本集合(可以是所有的未观测交互，也可以是从中采样的一部分)。wui是一个超参数，表示实例(u,i)的权重。使用squared loss可以解释为假设观测数据由一个高斯分布产生。
本文指出，对于implicit data，这种方式并不是特别合适。因为在implicit data中，目标值yu,i是binary的，表示用户u是否和物品i产生过交互。
本文提出了一种针对于implicit data的binary性质的损失函数。
用yu,i表示物品i与用户u相关，0表示不相关，预测score y ^ u,i表示物品i和用户u相关的程度。y ^ u,i的值在[0,1]之间，因此在output layer可以用sigmoid。
于是，定义likelihood为

损失函数为

(其实就是交叉熵)
用SGD进行优化。
对于负样本y-，在SGD的每次迭代中从未观测的数据中均匀采样，采样的数量与观测数据的数量相关。(文中提到一些非均匀采样策略可能会有更好的表现)

从NCF的角度来解释MF。pu表示用户u的embedding，qi表示物品i的embedding。将NCF的第一层定义为哈达玛积

然后将得到的向量映射到输出层

aout表示激活函数，h表示权重向量。如果令aout为identity function(即y=x)，令h为全1的向量，那么就得到了MF模型(相当于对pu和qi求内积)。
在NCF的框架下，MF可以被泛化和拓展。比如令h由数据学到，或者令aout为非线性函数。
文中，作者提出了GMF(Generalized Matrix Factorization)模型，令aout为sigmoid函数，令h从数据中学到，并使用log loss。

文中指出整合user和item的latent feature，如果仅仅是简单的concatenate(向量stacking)，或者像GMF中那样，使用固定的element-wise product(哈达玛积)，不能充分反映两者的交互关系。因此，文中提出在concatenate后，用MLP来学习它们的交互关系。

可以看到，第一层简单的把两者stacking起来，之后由MLP来进行特征整合，最后将整合得到的向量和每一维的权重向量h(由模型学习得到)相乘，再做sigmoid得到输出。
文中提出tower pattern的效果比较好，即下面的hidden层单元多，上面的hidden层单元少。文中使用的是，每上去一层，减半hidden层中的单元数。

考虑将GMF和MLP结合起来，更好的对复杂的user-item关系建模。
最简单最直接的方式就是让GMF和MLP共享同一个embedding layer，然后将两者的output结合起来。举个例子，结合GMF和一层MLP的模型如下

然而，让GMF和MLP共享embedding可能会限制融合模型的表现。比如说，这隐含了GMF和MLP必须有相同size的embedding。对于一些数据集，可能两者选择各自合适的embedding size会更好，这时候这种组合方式就不能够获得特别好的表现了。
为了能够更加灵活的结合两个模型，我们让GMF和MLP学习各自的embedding，结合两个模型通过整合各自最后的hidden layer。

pGu表示GMF部分的user embedding，pMu表示MLP部分的user embedding。
qGi表示GMF部分的item embedding，qMi表示MLP部分的item embedding。
在MLP部分，使用relu作为激活函数。
该模型结合了MF的线性和DNN的非线性，作者给其起名为NeuMF(Neural Matrix Factorization)。
模型参数的学习可以用标准的back-pop。

NeuNF的目标函数是非凸的，因此基于梯度的优化方法只能找到局部最优解。文中提出通过预训练GMF和MLP来初始化NeuMF。
首先随机初始化GMF和MLP来训练，直到收敛，然后用这些模型参数来初始化NeuMF中的相关部分。在output layer，整合两个模型的权重为

hGMF和hMLP分别表示预训练的GMF和MLP模型中的h。α是一个超参数。
具体的，预训练GMF和MLP时，使用了Adam，将模型参数输入到NeuMF做fine-tuning时，用SGD(因为Adam需要动量信息，而做完预训练后只保留了参数，没有保留动量相关信息)。

第九周.01.Neural Graph Collaborative Filtering

文章目录

• CF+GNN的原理
• 模型框架
• 论文泛读
• • 摘要
  • Introduction
  • 其他内容

本文内容整理自深度之眼《GNN核心能力培养计划》
公式输入请参考： 在线Latex公式
论文： Neural Graph Collaborative Filtering
PPT
代码
别人的翻译：https://www.jianshu.com/p/95da9785bea8
发表在19年的信息检索顶会SIGIR（International Conference on Research and Development in Information Retrieval）
本文主要涉及到一些推荐系统的知识，一些基本的概念这里不再详细介绍。
先讲主要思想：

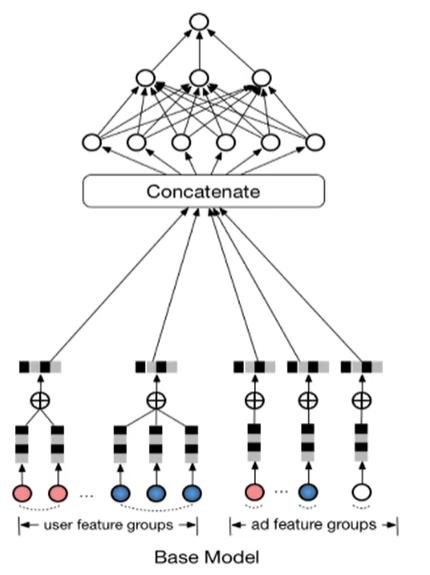
1、对于上面的Base Model而言，是把用户（User）和商品（Item，上图貌似是广告推荐）分开进行训练，得到的结果进行concat，这样的做法对于用户和商品的交互信息涉及较少，此为本文要改进的一点；

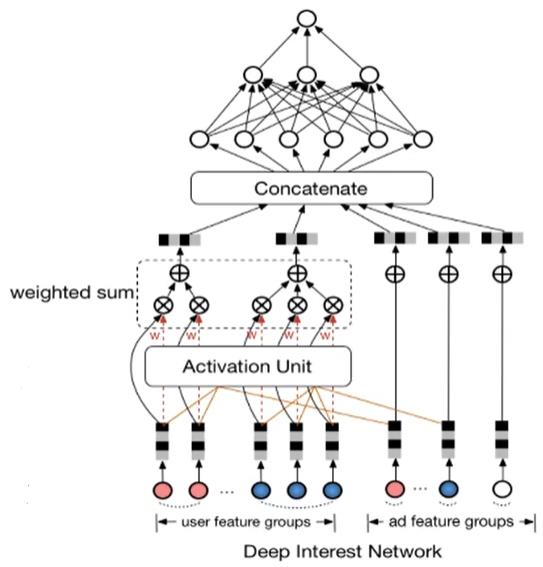
2、对于DIN模型来说，涉及到了一些用户交互信息，模型收集用户历史点击信息，用来和要购买的商品进行匹配，匹配的过程用到了注意力机制。该模型没有用到图的信息，但是从图网的角度来看，该模型仅用到了图的一阶相似度作为推荐依据。此为本文改进点二。
PPT中也总结了文章的贡献：
CF modeling with high-order connectivity via GNN.

CF+GNN的原理

撇开公式的推导，我们从PPT的一个例子来看看如何通过GNN来做协同过滤推荐。

这个是PPT里面的例子，我们看到$u_1$和$u_2$两个用户，分别购买了 { i 1 , i 2 , i 3 } \\{i_1,i_2,i_3\\} {i1​,i2​,i3​}和
{ i 2 , i 4 , i 5 } \\{i_2,i_4,i_5\\} {i2​,i4​,i5​}
如果我们把上面的关系看做图，那么就是一个Bipartite，
$u_1$的邻居是： { i 1 , i 2 , i 3 } \\{i_1,i_2,i_3\\} {i1​,i2​,i3​}
$i_2$的邻居是： { u 1 , u 2 } \\{u_1,u_2\\} {u1​,u2​}
$u_2$的邻居是： { i 2 , i 4 , i 5 } \\{i_2,i_4,i_5\\} {i2​,i4​,i5​}
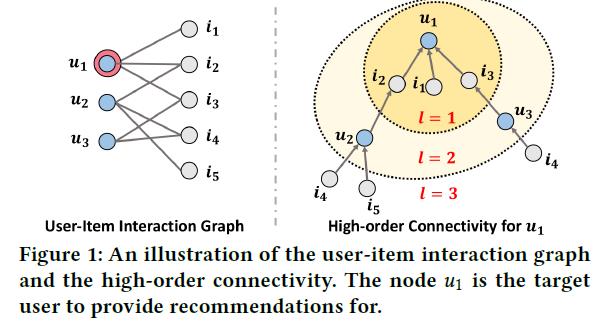
那么整合后可以看到$i_4$其实是$u_1$的高阶邻居（high-order connectivity），

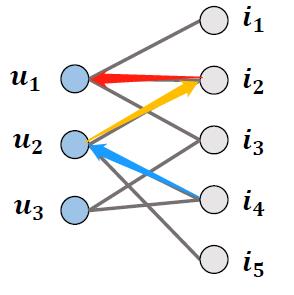
如果我们把图网的卷积传播放进来，那么经过3次卷积后，$i_4$的表征信息就会通过aggregate进入$u_1$，然后进行类似相似度计算的时候，$u_1$会比较倾向购买$i_4$。

从CF的角度来理解，$u_1$和$u_2$两个用户是同一类用户，二者会倾向于购买同一类商品，就好比两个宅男都会喜欢购买手办之类的。因此$u_2$购买过$i_4$，那么系统会向$u_1$也推荐$i_4$。

模型框架

左边$e_{u_1}$是用户1的表征，右边$e_{i_4}$是商品4的表征
这里作者将每一层（上图中是三层，用上标区分）计算出来的结果concat得到结果，然后将用户和商品的表征进行相似度计算得到Loss，进行反向传播。
The representations atdifferent layers
•emphasize the messages passed over different connections
•have different contributions in reflecting user preference
思考：将不同层的结果进行concat有什么好处？

论文泛读

摘要

两段式摘要。
第一段：开篇先说RS的核心任务是学习users and items的表征
Learning vector representations (aka. embeddings) of users and items lies at the core of modern recommender systems.
现有的方法：矩阵分解→DL，基本思想都是高维表征到低维表征的映射
Ranging from early matrix factorization to recently emerged deep learning based methods, existing efforts typically obtain a user’s (or an item’s) embedding by mapping from pre-existing features that describe the user (or the item), such as ID and attributes.
现有方法的缺点：交互信息collaborative signal难以被现有方法捕获。
We argue that an inherent drawback of such methods is that, the collaborative signal, which is latent in user-item interactions, is not encoded in the embedding process. As such, the resultant embeddings may not be sufficient to capture the collaborative filtering effect.

第二段，第一句就开门见山we propose 什么什么， We develop什么什么
In this work, we propose to integrate the user-item interactions — more specifically the bipartite graph structure—into the embedding process. We develop a new recommendation framework Neural Graph Collaborative Filtering (NGCF), which exploits the useritem graph structure by propagating embeddings on it.
然后点出创新点collaborative signa+high-order connectivity
This leads to the expressive modeling of high-order connectivity in useritem graph, effectively injecting the collaborative signal into the embedding process in an explicit manner.
最后摆出实验结果
We conduct extensive experiments on three public benchmarks, demonstrating significant improvements over several state-of-the-art models like HOPRec and Collaborative Memory Network. Further analysis verifies the importance of embedding propagation for learning better user and item representations, justifying the rationality and effectiveness of NGCF.

Introduction

给出了CF的概念：Collaborative filtering (CF) addresses it by assuming that behaviorally similar users would exhibit similar preference on items.
给出基于CF的两个关键：

1. embedding, which transforms users and items to vectorized representations.
2. interaction modeling, which reconstructs historical interactions based on the embeddings.
   为了更好的把collaborative signal进行融合，这里提出用用户商品之间的high-order connectivity来实现表征。
   然后在这里用$u_1$作为推荐对象给出了例子：
   

其他内容

METHODOLOGY这节就是模型的数学表达，里面的内容基本都在图网里面讲过，不重复了，稍微点一下
2.1讲的是模型的输入
2.2.1First-order Propagation.实际上是GNN的单层卷积表示
这里要提一下公式2里面有一个变量：$p_{ui}$这个表示discount factor，实际就是一个权重，例如张三喜欢周杰伦，我们推断李四是否喜欢周杰伦。由于周杰伦基本大家都喜欢，跟张三李四是不是同一类用户其实关系不大，因此这里就要对周杰伦参与计算加入discount factor。
另外在公式4里面的$m_{u\leftarrow u}$代表节点self aggregate。
2.2.2 High-order Propagation.实际上是GNN的多层卷积
2.3就是对上面模型框架图的讲解。
2.4.1Model Size对模型的参数个数进行了分析，$2L{d}_l{d}_{l-1}$，其中$L$是GNN的层数，$d_l$是表征维度，比起基线的参数量相比，并没有增加多少。
2.4.2消息和节点的抓爆，这个第一次看到，有点意思。
2.5.2时间复杂度分析，第一部分是GNN卷积计算的时间复杂度，第二部分模型的prediction layer的时间复杂度