图论--05:最短路径问题（Floyd算法）

Posted 2021-04-28 株洲市二中信息技术教研组

• 描述

• 面上有n个点（n<=100），每个点的坐标均在-10000~10000之间。其中的一些点之间有连线。

  　　若有连线，则表示可从一个点到达另一个点，即两点间有通路，通路的距离为两点间的直线距离。现在的任务是找出从一点到另一点之间的最短路径

• 输入

• 　第一行为整数n。 
  　　第2行到第n+1行（共n行） ，每行两个整数x和y，描述了一个点的坐标。 
  　　第n+2行为一个整数m，表示图中连线的个数。 
  　　此后的m 行，每行描述一条连线，由两个整数i和j组成，表示第i个点和第j个点之间有连线。 
  　　最后一行：两个整数s和t，分别表示源点和目标点。

• 输出

• 仅一行，一个实数（保留两位小数），表示从s到t的最短路径长度。

• 样例输入

• 5 0 0 2 0 2 2 0 2 3 1 5 1 2 1 3 1 4 2 5 3 5 1 5 

• 样例输出

• 3.41

试题分析：

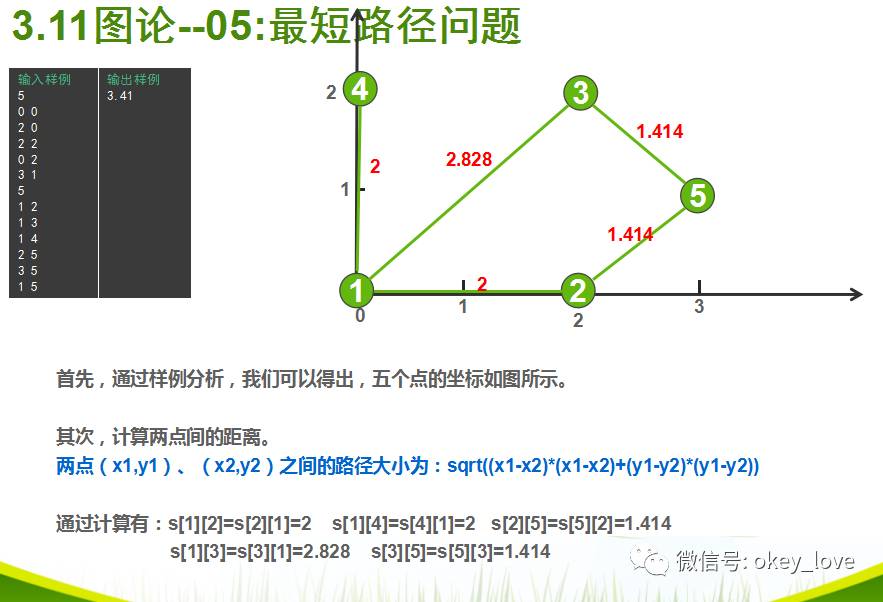
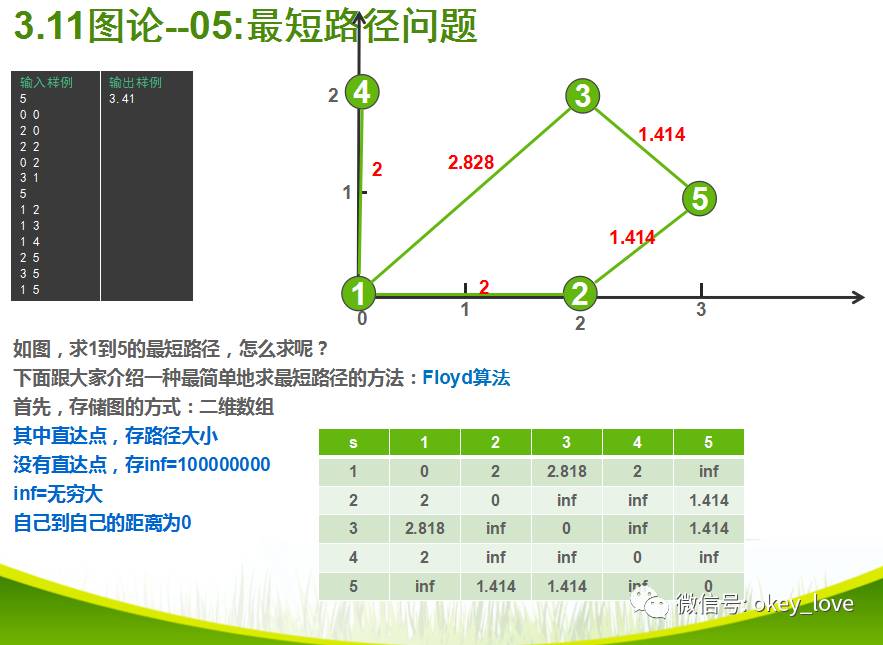
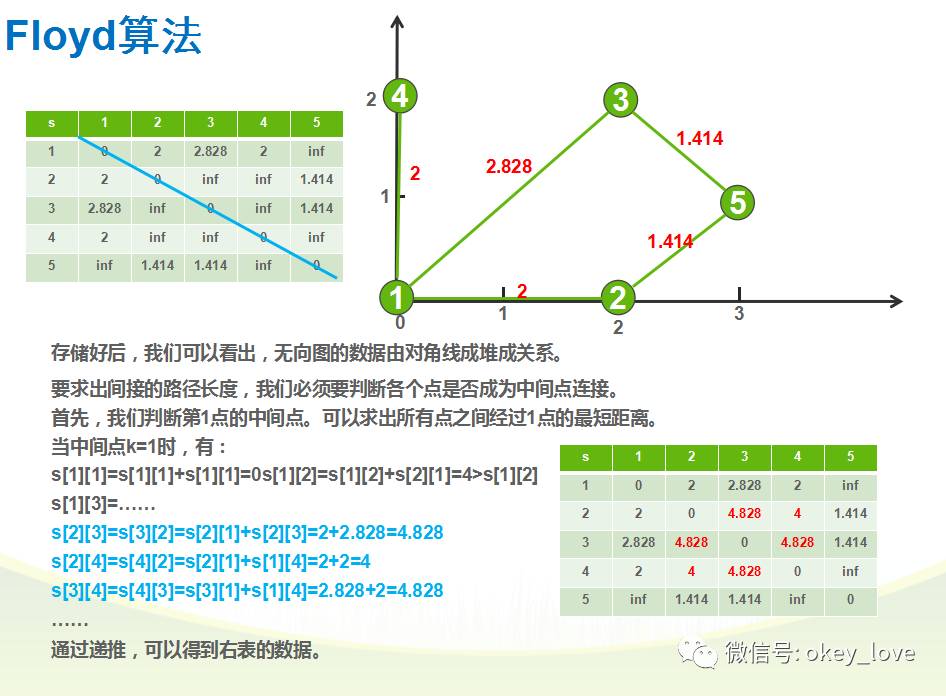
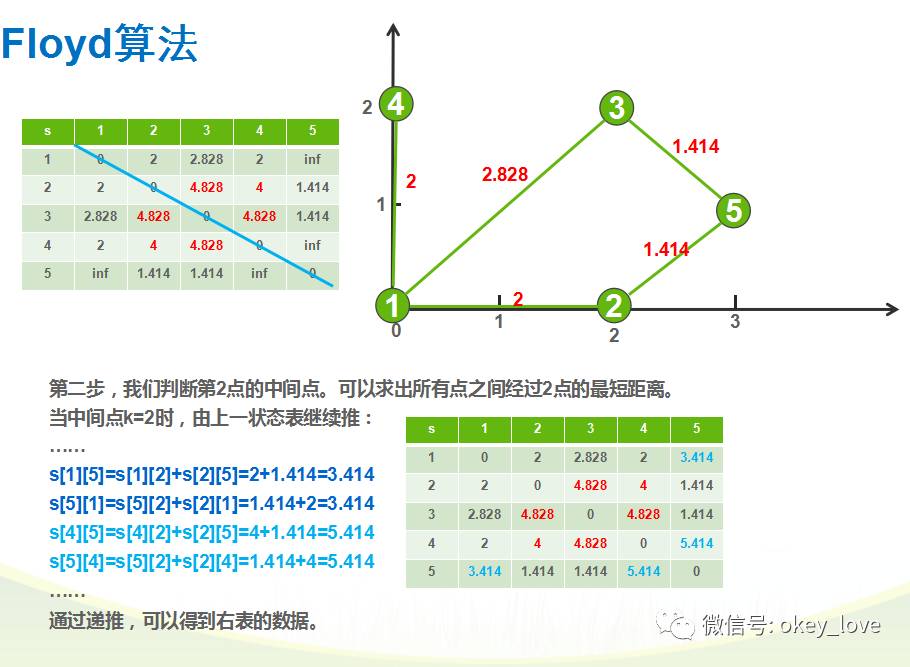
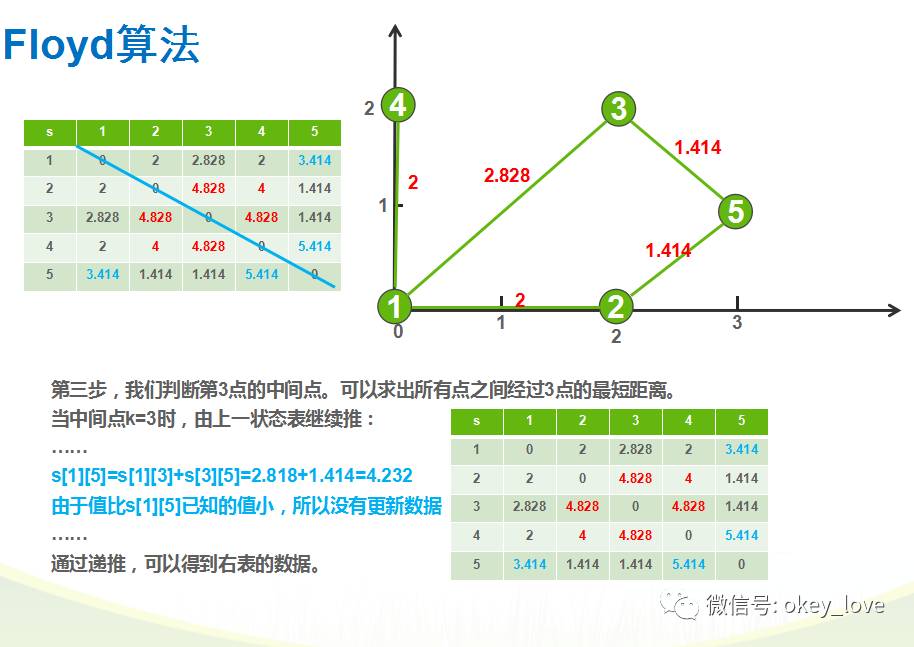
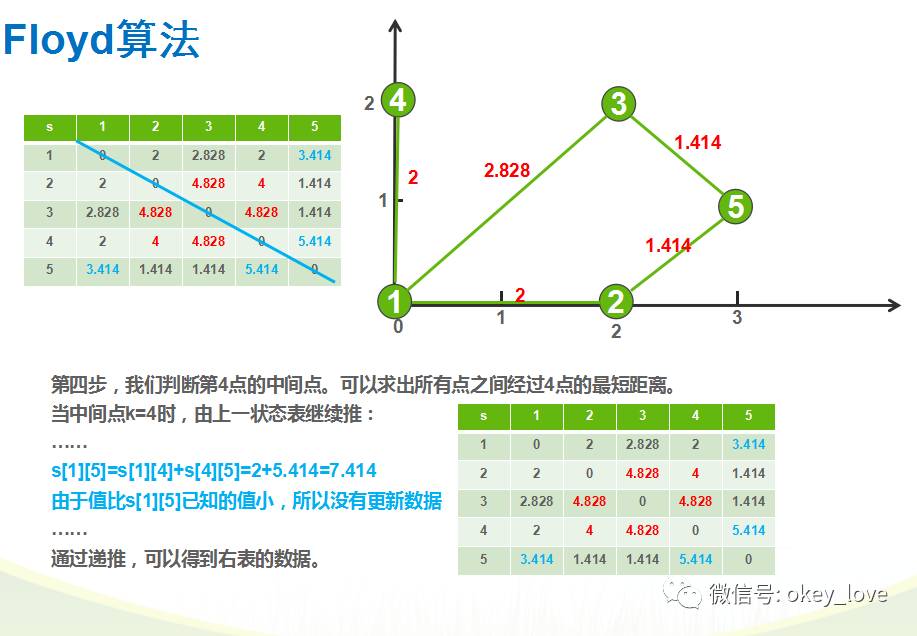
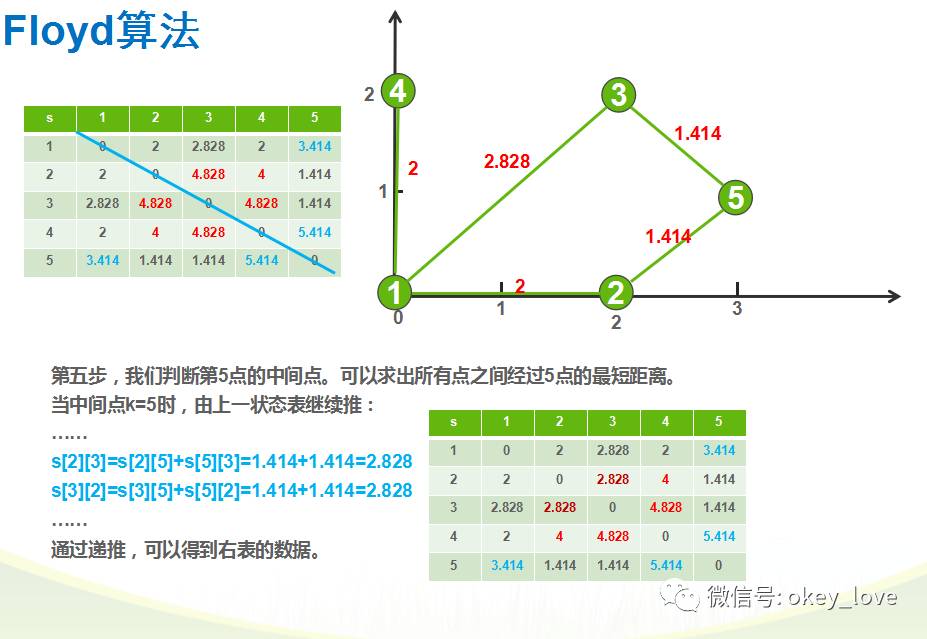
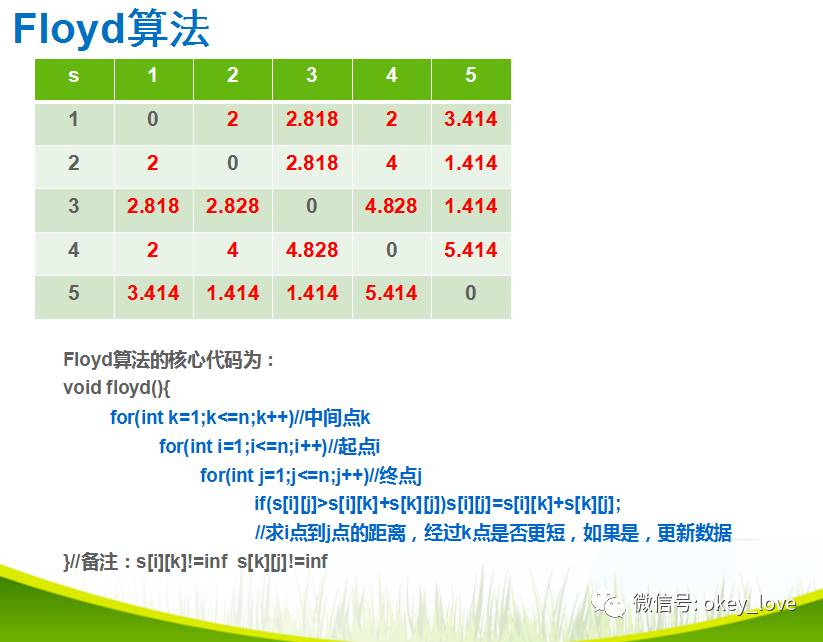
参考程序：

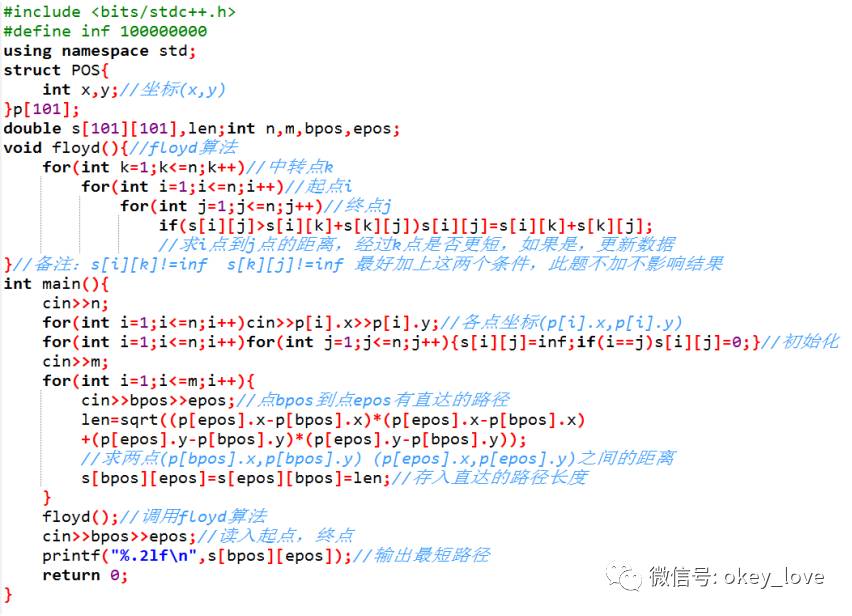
图文编辑：陈鸥辉老师