最短路径（几何最值）问题难点突破——中考数学压轴题

Posted 2021-04-28 中考数学压轴题

以下是人教版八年级上的教材截图：

问题简化如下所示：

如图，A和B两地在一条河的两岸，现要在河上建一座桥CD，桥造在何处才能使从A到B的路径ACDB最短？  （假设河的两岸是平行的直线，桥要与河垂直）

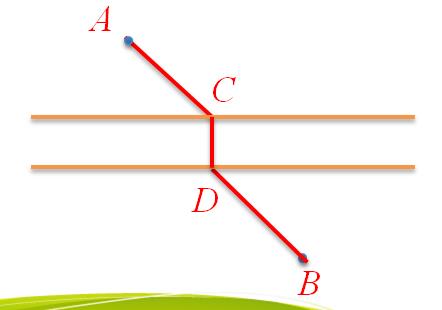
应该怎么做呢？请看下面的视频演示：

但是一般中考题中会换一种说法。例如：

②如图所示，长度不变的线段CD在直线l上运动，在直线l上找到使得AC＋BD最小的CD的位置．分别过点A，D作AA′∥CD，DA′∥AC，AA′与DA′交于点A′，再作点B关于直线l的对称点B′，连接A′B′与直线l交于点D′，此时点D′即为所求．

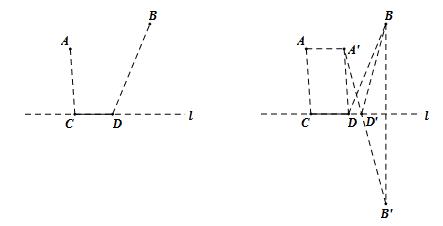
解析可以看视频演示：

总结一下：

过两动点与一个定点构造平行四边形。把两条分开的线段其中一条进行平移，使他们有公共点，再利用将军饮马模型即可解决。

【典型例题】

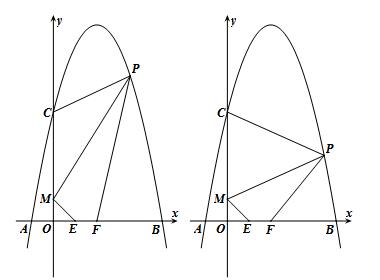
1．（14海南）如图，对称轴为直线x＝2的抛物线经过A（－1，0），C（0，5）两点，与x轴另一交点为B．已知M（0，1），E（a，0），F（a＋1，0），点P是第一象限内的抛物线上的动点．

（1）求此抛物线的解析式；

（2）当a＝1时，求四边形MEFP的面积的最大值，并求此时点P的坐标；

（3）若△PCM是以点P为顶点的等腰三角形，求a为何值时，四边形PMEF周长最小？请说明理由．