最短路径大综合（八年级）

Posted 2021-04-28 老傅教难题

（点击“老傅教难题”关注）

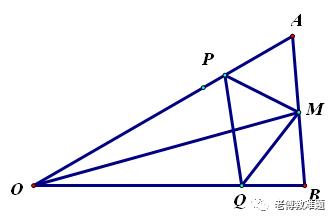
已知：点M是锐角△AOB的边AB上任意一点。

（1）请在OA边上求作一点P，在OB边上求作一点Q，使得△PMQ的周长最小.如果OM=2，∠AOB=30°，求此时△PMQ的周长.

（2）当点M 在边AB上运动时，请研究△PMQ的周长何时会取得最小.如果AB=3，∠AOB=30°，△AOB的面积为6，求此时△PMQ的周长的最小值.

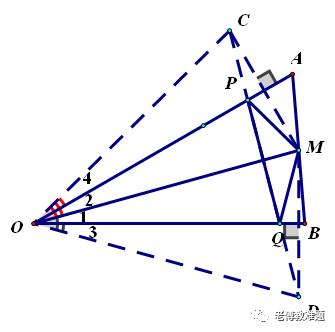
分析（1）：利用轴对称性确定点P、Q的位置

解：（1）分别作点M关于OA、OB的对称点C、D.连CD分别交OA、OB于P、Q两点，连MP、MQ.则点P、Q即这所求，△PMQ的周长最小.

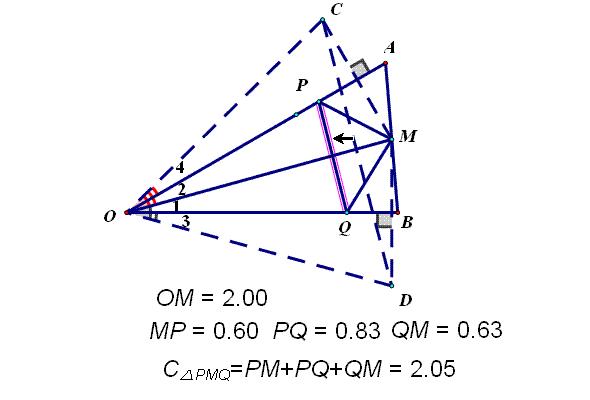
构造等边三角形求最小值

连CO、DO，由对称性知：PM=CP，QM=DQ，OM=OC=OD=2，

∠1=∠3，∠2=∠4.

∴△PMQ的周长=PM+PQ+QM=CP+PQ+QD=CD

∵∠AOB=∠1+∠2=∠3+∠4=30°

∴∠COD=60°

∴△COD为等边三角形

∴CD=OC=2

∴此时△PMQ的周长为2.

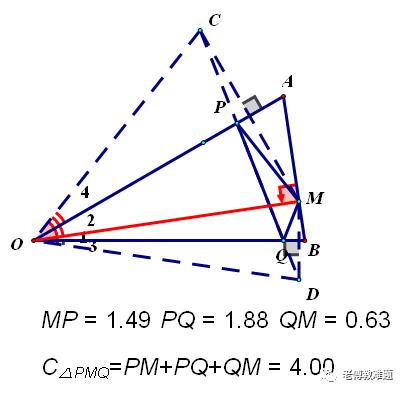
分析：（2）根据“垂线段最短”得：当OM⊥AB时，OM最小

解：（2）当∠AOB=30°时，由（1）得△PMQ的周长=CD.△COD为等边三角形，OC=OM

∴△PMQ的周长=CD=OC=OM.

∴据“垂线段最短”得：当OM⊥AB时，△PMQ的周长取得最小.

利用面积求高OM

拓展提高

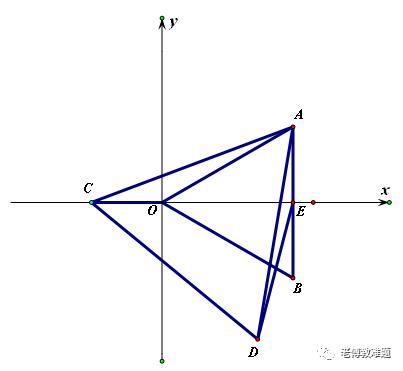
分析：先观察点D的运动轨迹

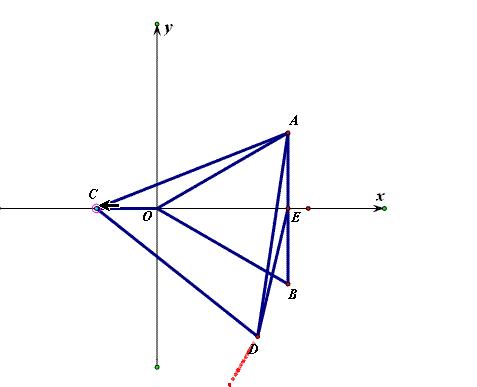
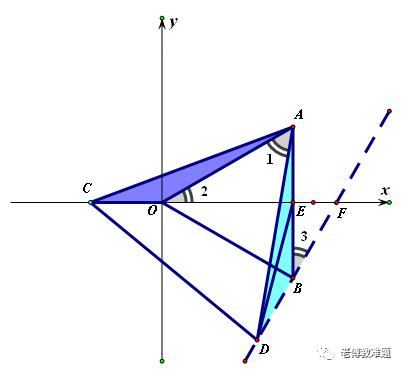
∴据“垂线段最短”得：当ED⊥BF时，ED最小.

此时∠EDB=90°，∠3=30°.

∴ED=EB÷2=1.

∴ED的最小值为1.

最短距离的动态演示图（当ED⊥BF时，ED最小.）

小结：

（1）定点到定点的最短路径是根据“两点之间，线段最短”.

（2）定点到直线上的动点的最短路径是根据“垂线段最短”