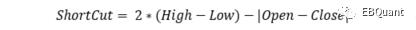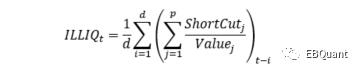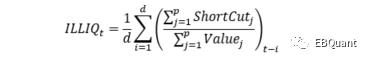基于K线最短路径的非流动性因子

Posted 2021-04-28 EBQuant

多因子系列报告之七 

特别提示 ：本订阅号中所涉及的证券研究信息由光大证券金融工程研究团队编写，仅面向光大证券客户中专业投资者客户，用作新媒体形势下研究信息和研究观点的沟通交流。非光大证券专业投资者客户，请勿订阅或使用本订阅号中的任何信息。

随着对金融市场的研究不断深入，数目众多的选股因子早已被研究者与市场参与者们挖掘出来。然而近年来数据维度的不断提升，又使得我们回头重新审视那些作为股票属性代理变量的因子，它们的代理精度是否可以再次提升？选股效果能否得以再次加强？本篇报告将利用高频数据的信息，构造代理精度更高的非流动性因子——K线最短路径非流动性因子。

经典的非流动性代理变量在日内震荡行情下失效

大类因子测试主要结论

经典的非流动性因子定义方式（Amihud, JFM 2002）：

该定义方式的逻辑在于试图通过单位成交量对收益率的影响，来刻画该股票交易的市场冲击，从而间接描述该股票的非流动性。在A股中，该非流动性定义方式是有效的选股因子，在移动平均参数d=5时，其因子IC均值4.25%，IR值0.46。但从它的定义本身出发，其刻画方式有着一定程度的缺陷。

如果当日的交易处于单边上涨或单边下跌，经典定义方式可以较好地度量交易对股票价格的市场冲击；但如果遇到当日日内震荡，股票上涨时的价格变动与下跌时的价格变动方向相反从而相互抵消，而成交量却没有方向继续累加，此时经典定义方式并不能有效地度量当日该股票的交易对其价格的市场冲击，从结果上会严重低估该股票的非流动性。

用K线最短路径近似描述市场冲击总量

经典定义的非流动性代理变量的缺陷在于会在日内震荡行情下失效。而终其根本失效的原因则在于，分子部分中收益率的形成为逐笔交易收益的有向叠加，而分母部分中成交量的形成则为无向叠加。叠加方式的不同，造成了经典定义有效性对于日内行情的极度依赖。容易想到，如果能让分子与分母的叠加方式一致，将很大程度上克服经典定义遇到的难题。方式一致的情况有两种：全部变成有向叠加，或全部变成无向叠加。

但是通过将收益率的正负号赋给成交量的方式而形成的有向叠加仍旧有着负值因子（作为单位成交量下的市场冲击代理变量，出现负值显然并没有逻辑意义）与零值分母（因子值在分母接近零值时极度不稳定，分母微小的变动会对因子值造成巨大改变）等诸多弊端。

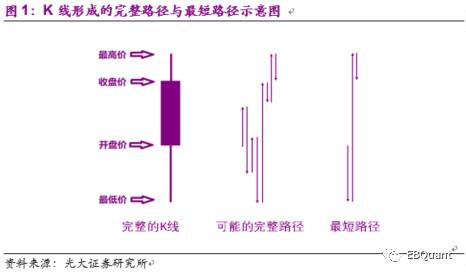
既然将分子分母全部变成有向叠加的方式并不适合。而采用无向叠加的方式又不会出现上述讨论的缺陷。因此我们定义新的代理变量时将使用全部变成无向叠加的方式。我们认为股票在一个时间段里价格所经历的完整路径长度，很好地体现了该段时间内交易造成的市场冲击总值。而在仅有一个完整K线的情况时，且没有K线完整路径长度分布的信息下，我们能够得到的最确定的接近完整路径长度的值为股票形成该K线的最短路径长度（ShortCut），即：

在在一根K线上，我们定义在该K线的时间段上，非流动性的代理变量为单位成交额下的最短路径长度。容易想到，如果一根K线能分解成频率更高的多跟K线，那么高频K线的最短路径就更接近于完整路径。使用高频K线下，如15分钟、5分钟等，计算我们定义下的非流动性代理变量将得到更高的精度。此时每日的K线最短路径非流动性因子定义为：

高频数据下因子改善效果显著

大类因子测试主要结论

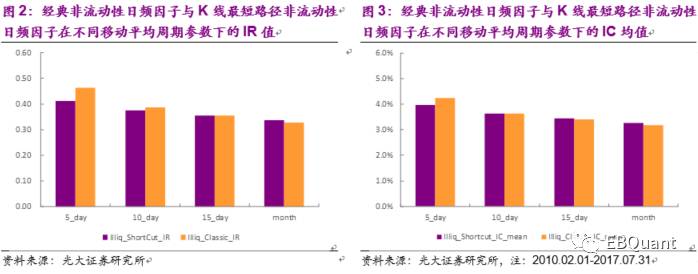
在日频数据下，K线最短路径非流动性因子与经典非流动性因子之间对于股票相对收益的预测能力的差异较小。在5日MA下，经典因子的IC均值与IR值甚至超过了K线最短路径非流动性因子。

我们认为造成这种情况的原因可能主要是由于以下两点：1）在日频下，即使是K线最短路径长度，也与K线完整路径长度大概率相差太远。即使使用K线最短路径的定义，对非流动性的刻画提升程度也有限。2）经典定义中使用的收益率，本身带有其它一些Alpha因子效应。利用收益率构造的因子可能会从中收益。当其它非流动性因子通过对非流动性刻画的提升带来的收益不足以覆盖收益率自身可能带来的收益时，那么可能使用它的最终效果反而不如直接使用经典非流动性因子好。

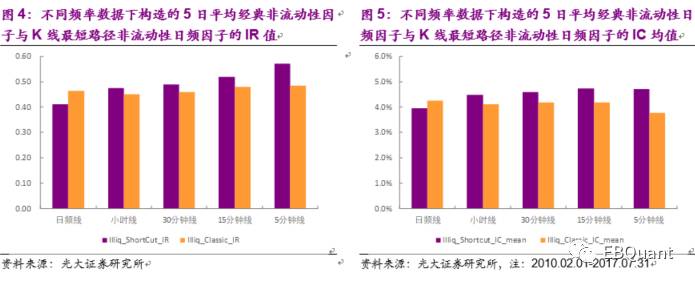
依此使用1小时K线，30分钟K线，15分钟K线与5分钟K线分别计算K线最短路径非流动性因子与经典因子并测试其因子效果统计数据。从实证结果中，我们得到一下几个结论：首先，无论在哪个频率的数据下，因子的IC均值与IR值都是随着使用的移动平均周期参数减小而增大，在测试的几个MA参数中，使用5日平均的效果最好。其次，因子的IR值无论在哪个MA参数下，都随着使用数据频率的增大而单调增加，且有较强的线性关系。与IR值类似，因子的IC均值也基本上随数据频率的增大而增加。

从上图可知，K线最短路径非流动性因子的IC均值与IR值在小时线频率时均超过经典非流动性因子。并随着使用频率的不断提高，两种非流动性因子的IC均值与IR值之间的差距单调扩大。这是因为比起经典的定义方式，K线最短路径能更充分地利用高频数据新引入的信息。

K线最短路径非流动性因子其它变化的尝试

大类因子测试主要结论

前文我们已阐明了K线最短路径非流动性因子的具体构造方式，在本节中我们研究在原有定义方式上的一些变形，看看不同变形下因子的效果。

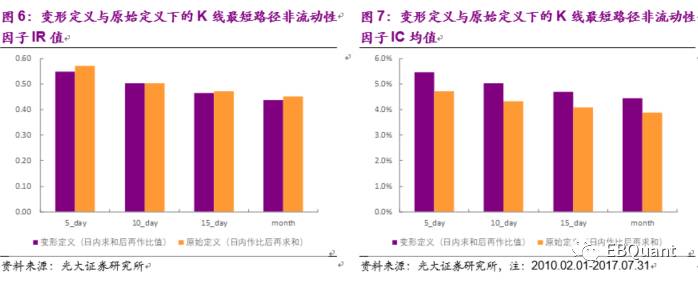
首先，我们尝试在做移动平均的操作时采用加权移动平均的方式来替代原先使用的简单移动平均。从IR及IC均值来看，两种不同移动平均方式对因子效果影响很小。其次，我们尝试将定义中括号内部分的求和与求比的操作顺序调换，即将K线最短路径非流动性因子定义变形为：

从测试结果来看，原始定义与变形定义各有优劣。从IC均值的角度来说，变形定义的IC均值明显高于原始定义，表明变形定义下的因子预测性更好。但由于变形定义下IC标准差过大，其IR值并没有得到提高。

K线最短路径因子选股与预测能力较强

大类因子测试主要结论

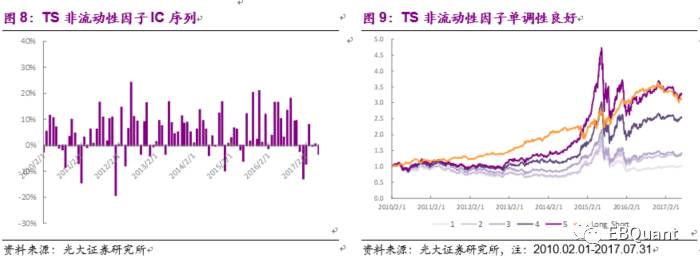
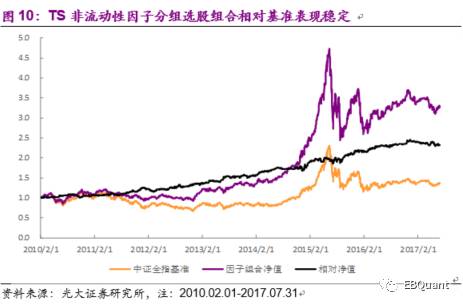
通过对各种定义下的K线最短路径非流动性因子多空组合表现的比较，我们将调换过计算顺序但未经移动平均操作的K线最短路径非流动性因子确定为我们最终的选股因子。为了之后描述方便，我们称其为TS非流动性因子（Transformed-Shortcut）。TS非流动性因子IC均值与IR分别高达6.5%与0.72。从它的选股组合分组净值可以看出其单调性也较佳。

将5组分组中的第5组作为我们的选股组合，在2010年至2017年间，年化收益18.2%，年化波动率24.8%，夏普比率0.8，最大回撤48.3%，月度换手率31.4%。相对中证全指年化收益12.5%，相对波动率8.3%，相对最大回撤仅8.35%。

为了了解有哪些已有因子与TS非流动性因子有较高的相关性，我们分别计算了规模因子、动量因子、技术因子、波动因子及流动性因子中单因子测试显著性较高的几个因子与TS非流动性因子之间历史IC值的相关系数。从结果上看，代表流动性因子的VSTD以及代表规模的市值因子与TS非流动性因子相关性都很强，相关系数分别为 -0.55与 -0.34。这与大众认知观念是相一致的，小市值股票的流动性一般弱于大市值股票。而换手，动量，波动率等因子与TS非流动性因子的相关系数基本在0.1到0.15之间。

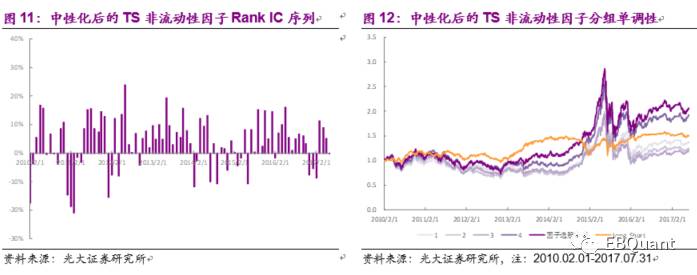
对TS非流动性因子做行业、市值中性处理并剔除换手、动量等因素的影响后，因子的有效性检验等结果有不小下降，但依然显著，IC平均值为3.5%，，IR值为0.39。分组依旧有一定单调性，然而相比中性化之前，最低3组的单调性结果较差；多空组合年化收益亦有所下降为5.52%，夏普比率则大幅下降至0.52。中性化处理后的TS非流动性因子选股能力从收益上看有不小下滑，年化收益仅为10.14%。波动也有小幅扩大，年化波动率为26.08%，夏普比率0.50。

综上，TS非流动性因子在剔除其它类型因子的整体效果有较大程度地回撤，但依然包含大量的独有信息。同时该因子还有着较大的提升空间。实际上，在每根K线至少包含3次交易的情况，提高K线的频率基本上都能够提升K线最短路径对该股票交易的市场冲击模拟精度，进而提升以此构造的非流动性因子的有效性与预测能力。可以预见，如果得以运用1分钟甚至更高频的的K线数据，K线最短路径非流动性因子的预测能力与选股效果能够进一步加强。

更多详细内容敬请参考光大金工的完整报告《基于K线最短路径构造的非流动性因子——多因子系列报告之七》

联系人： 胡骥聪 

邮箱： [e-mail] 

特别声明：本订阅号由光大证券金融工程研究团队编写，所刊载的信息均基于光大证券研究所已正式发布的研究报告，仅供在新媒体形势下研究信息、研究观点的及时沟通交流，其中的资料、意见、预测等，均反映相关研究报告初次发布当日光大证券研究所的判断，可能需随时进行调整，本订阅号不承担更新推送信息或另行通知的义务，任何情况下任何完整的研究观点，均应以光大证券研究所已正式发布的相关研究报告为准。

本订阅号仅面向光大证券专业投资者客户。光大证券客户中非专业投资者客户，不论通过何种渠道阅读到本订阅号的内容，请自行评估相关内容适当性，并咨询专业投资顾问，对相关信息可能的风险进行充分的了解，若因不当使用本订阅号中任何信息而造成任何直接或间接损失，需自行承担全部责任。非光大证券客户，请勿订阅或使用本订阅号中的任何信息。