蚂蚁很忙——几何体的最短路径问题

Posted 2021-04-28 初中数学小魔方

      在数学的世界里，有一只蚂蚁真的很忙，简直称得上“劳模”．这不，刚刚从立方体、长方体表面下来，它又踏上了新的征程——在圆柱、圆锥的侧面爬行．圆柱、圆锥与立方体、长方体最大的区别就在于前者的侧面是曲面，而后者都是平面．那怎么解决这类问题呢？我们仍然要借助展开图（侧面），将曲面转化为平面，难题就迎刃而解了．

例1

在底面半径为1、高为4的圆柱中，一只蚂蚁从A点出发，沿圆柱的侧面爬行一周到达与A同一条母线上的另一个端点B处，问蚂蚁爬行的最短路径长为多少？

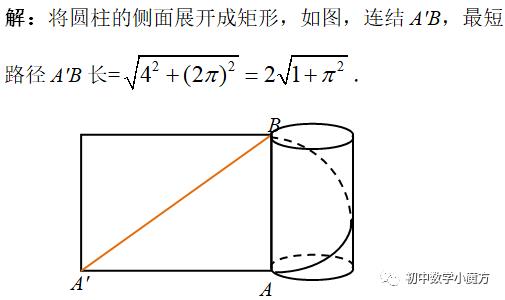
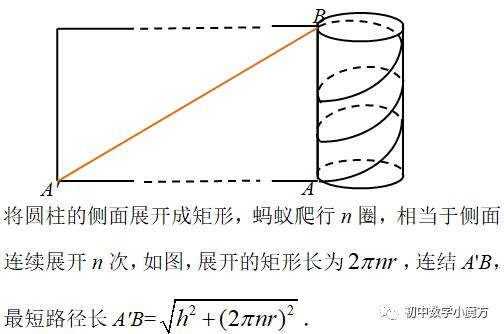
在底面半径为r、高为h的圆柱中，一只蚂蚁从A点出发，沿圆柱的侧面爬行n圈到达与A同一条母线上的另一个端点B处，问蚂蚁爬行的最短路径长为多少？

例2

如图，在底面直径BC为2、母线长为3的圆锥中，一只蚂蚁从C点出发沿侧面爬行到母线AB的中点D处，问蚂蚁爬行的最短路径长为多少？

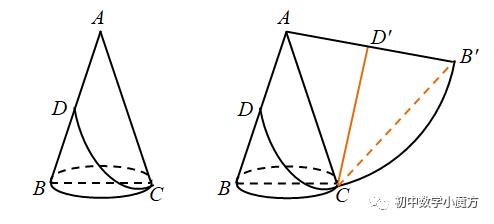
      总而言之，无论是正方体、长方体还是圆柱、圆锥，解决最短路径问题的本质都是相同的．在解决最短路径问题时，先确定蚂蚁在几何体的哪些面上爬行（必要的时候进行分类讨论），然后在同一平面内将这些面展开，根据两点之间线段最短（或垂线段最短），将复杂的路径最短问题转化为简单的求线段长问题即可．当然，我们也要清楚的知道，圆柱的侧面展开图是矩形，而圆锥的侧面展开图是扇形，同时也要掌握侧面与展开图之间的一些数量关系．

      说到这里，在以后的学习中，看到几何体中最短路径的你，再也不会害怕了吧！想想这只勤劳的蚂蚁，想想它教会你的，相信无论是蚂蚁苍蝇，还是蜘蛛螳螂，你都能轻松解决哦！

思考题

如图，圆柱形容器高为18cm，底面周长为24cm，在杯内壁离杯底4cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿2cm与蜂蜜相对的点A处，求蚂蚁从外壁A处到达内壁B处的最短距离．

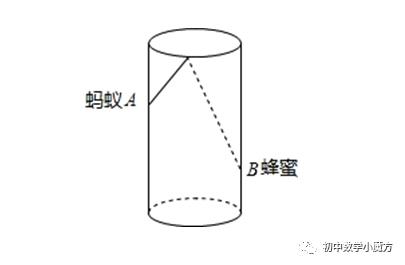
End