抛物线压轴题最短路径面积最值问题

Posted 2021-04-28 老杨和数学的故事

抛物线压轴题

最短路径、面积最值问题

2018.1.17

（2016•湘西州）如图，长方形OABC的OA边在x轴的正半轴上，OC在y轴的正半轴上，抛物线y=ax²+bx经过点B（1，4）和点E（3，0）两点．
（1）求抛物线的解析式；
（2）若点D在线段OC上，且BD⊥DE，BD=DE，求D点的坐标；
（3）在条件（2）下，在抛物线的对称轴上找一点M，使得△BDM的周长为最小，并求△BDM周长的最小值及此时点M的坐标；
（4）在条件（2）下，从B点到E点这段抛物线的图象上，是否存在一个点P，使得△PAD的面积最大？若存在，请求出△PAD面积的最大值及此时P点的坐标；若不存在，请说明理由．

解法提示

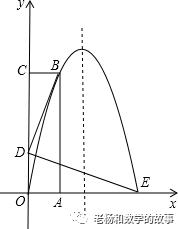
（1）将点B（1，4），E（3，0）的坐标代入抛物线的解析式，得到关于a、b的方程组，求得a、b的值，从而可得到抛物线的解析式；
（2）依据同角的余角相等证明∠BDC=∠DE0，然后再依据AAS证明△BDC≌△DEO（即：一线三等角），从而得到OD=AO=1，于是可求得点D的坐标；
（3）将军饮马问题：

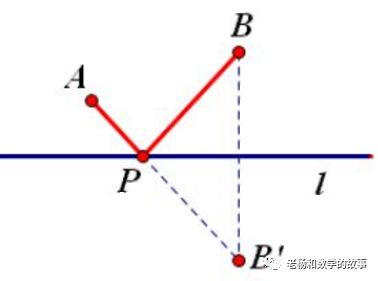
作点D关于抛物线的对称轴的对称点D′，连接D′B交抛物线的对称轴与点M．先求得抛物线的对称轴方程，从而得到点B′的坐标，由轴对称的性质可知当点B、M、D′在一条直线上时，△BMD的周长有最小值，依据两点间的距离公式求得BD和BD′的长度，从而得到三角形的周长最小值，然后依据待定系数法求得直线D′B的解析式，然后将点M的横坐标代入可求得点M的纵坐标；
（4）提供四种思路：

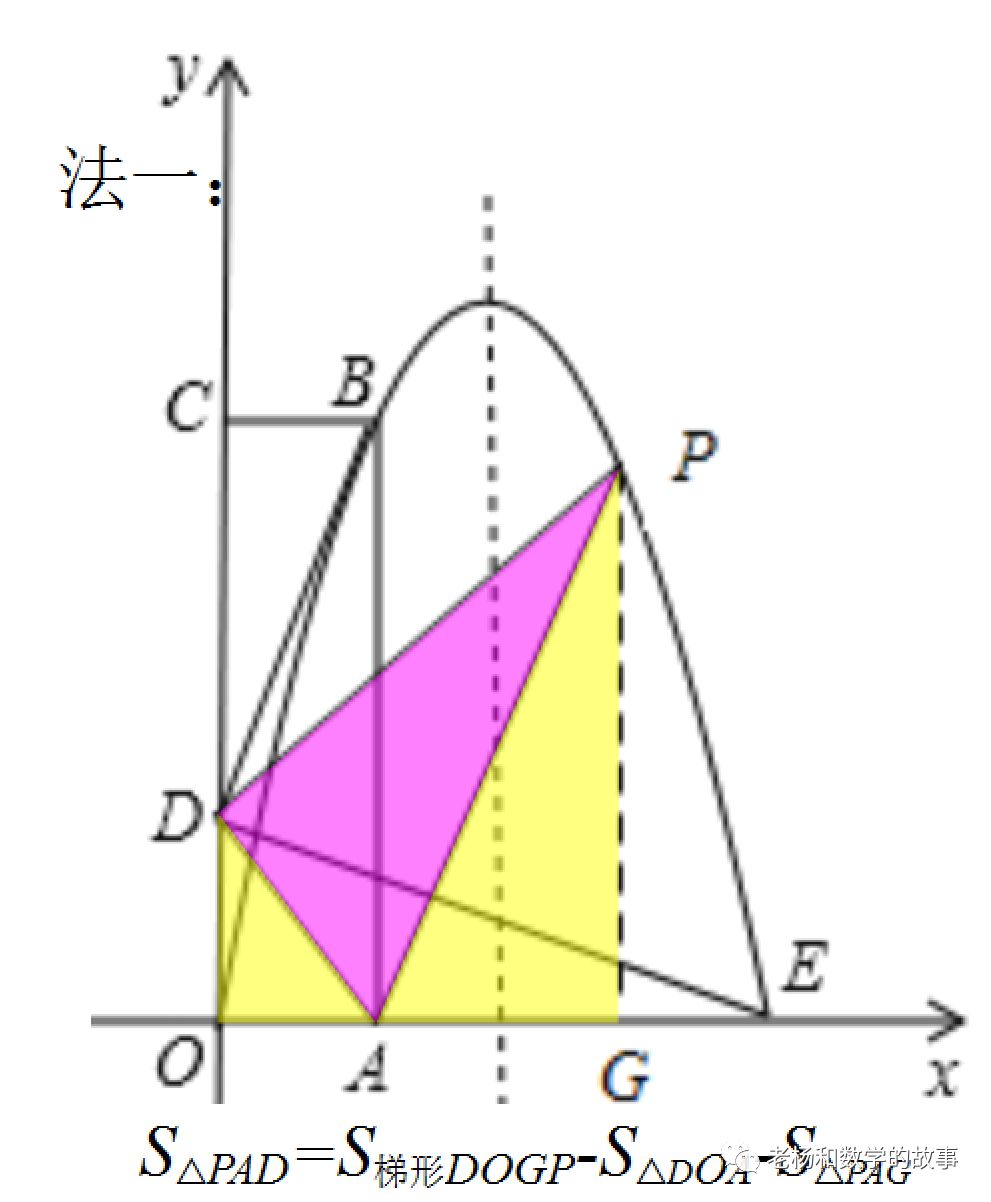
方法一：过点P作PG⊥x轴，垂足为G．设点P（a，-2a²+6a），则OG=a，PG=-2a²+6a．然后依据S_△PAD=S_梯形DOGP-S_△ODA-S_△AGP的三角形的面积与a的函数关系式，然后依据二次函数的性质求解即可，如下图法一。

        

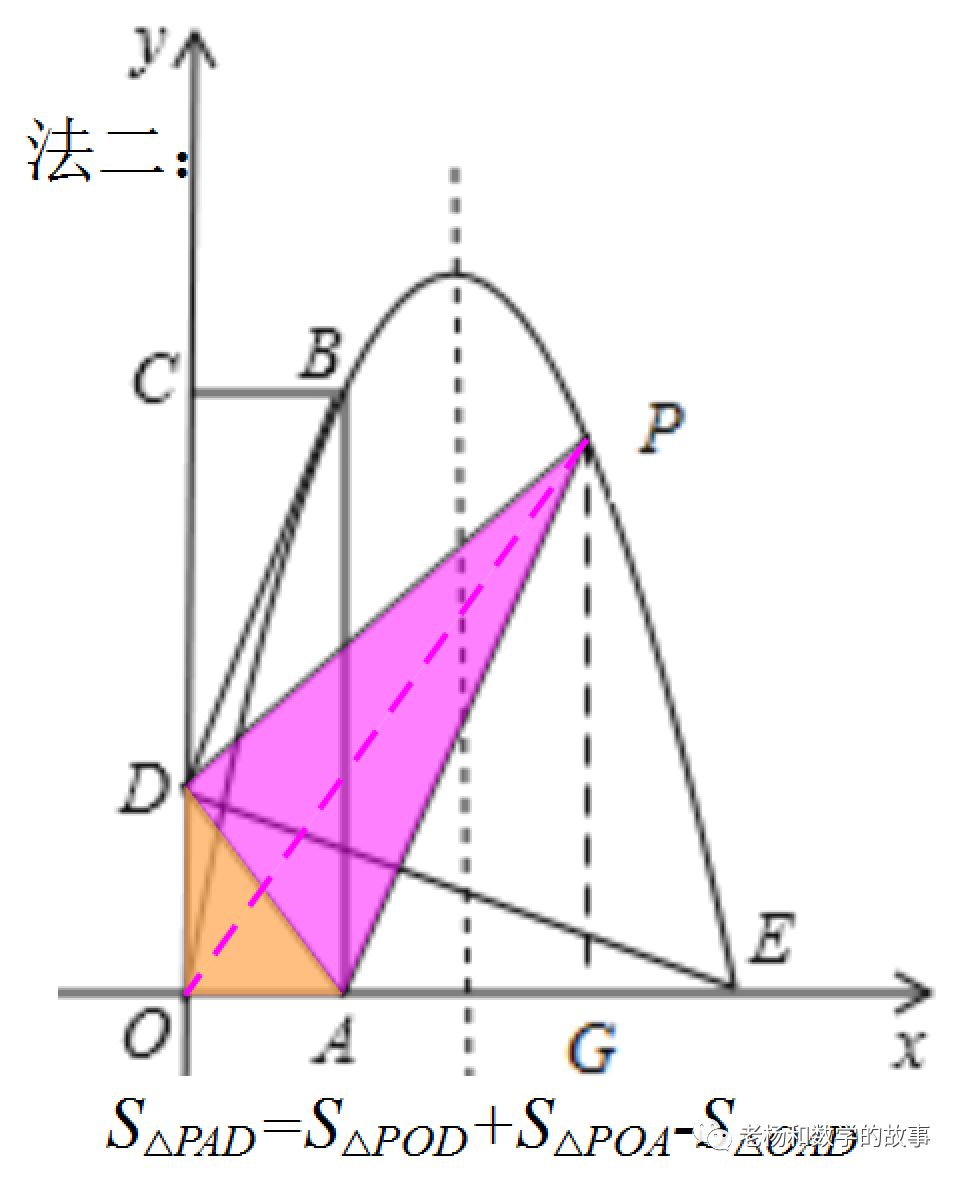
方法二：如上图法二，连接OP．设点P（a，-2a²+6a），则OG=a，PG=-2a²+6a．然后依据S_△PAD=S_△POD+S_△POA-S_△OAD得到面积与a的函数关系式，然后依据二次函数的性质求解即可。

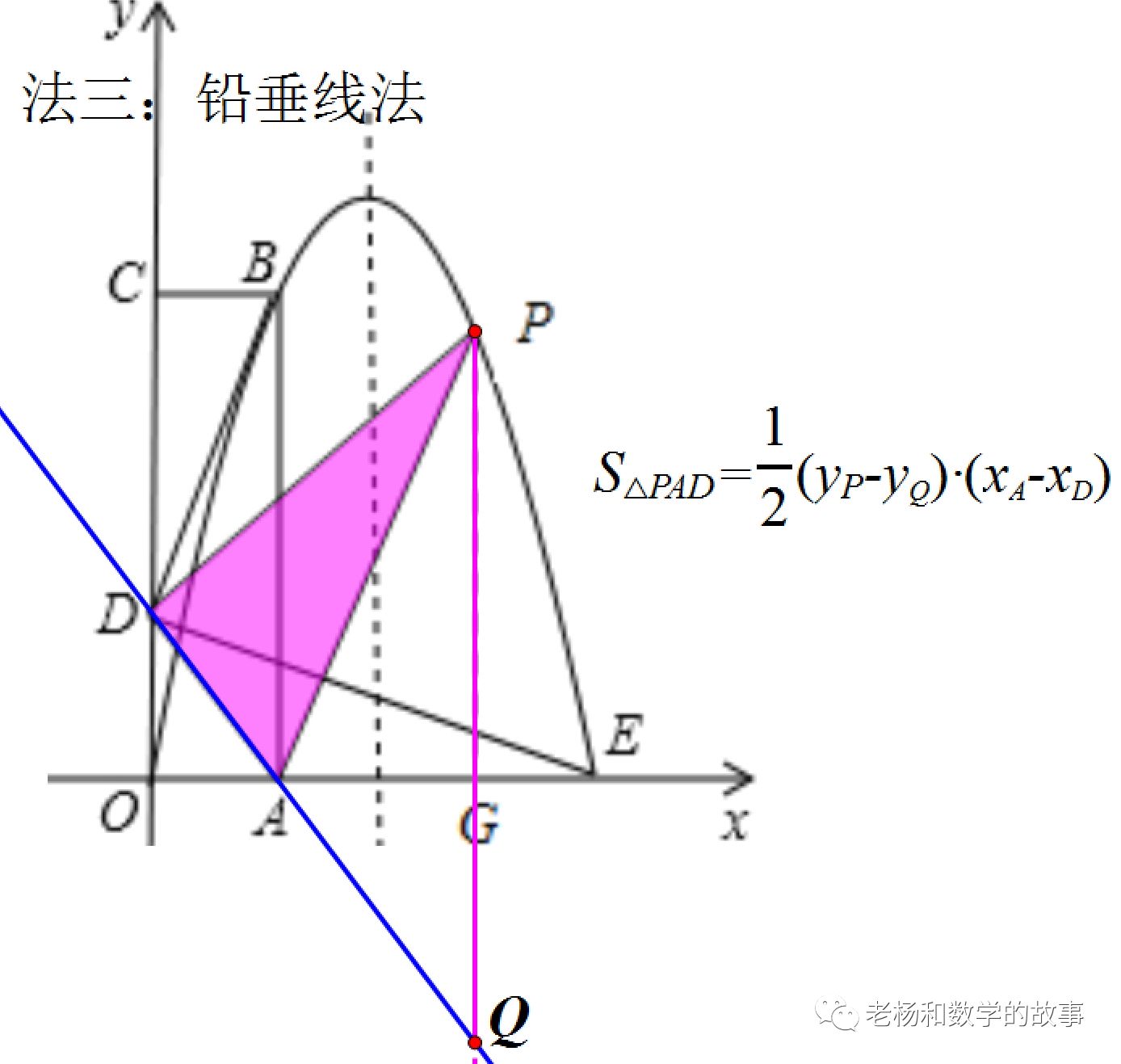
方法三：铅垂线法。过P作x轴的垂线，交直线AD于点Q，则：

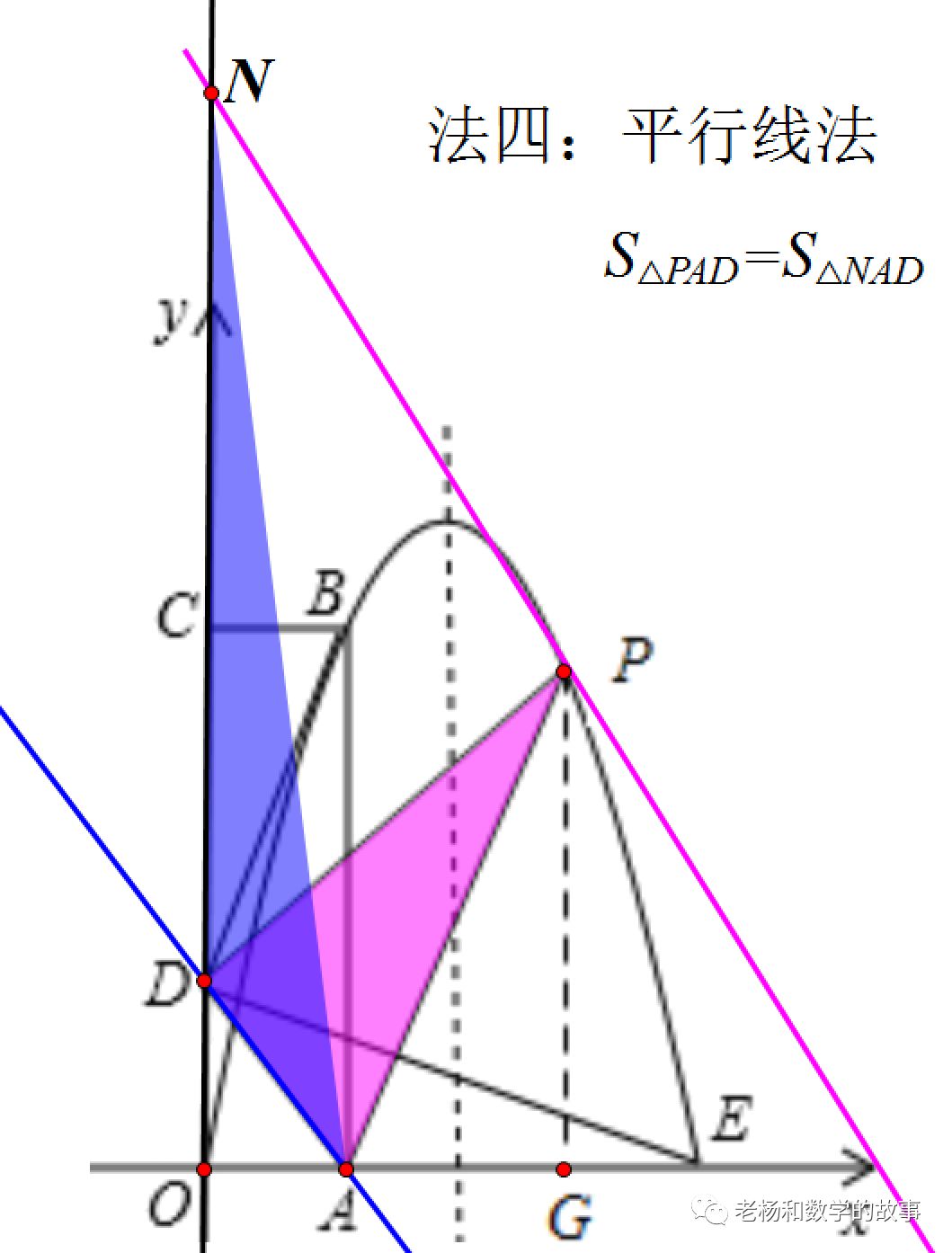
方法四：平行线法。过P作底边AD的平行线PN交y轴于N，则PN的解析式y=kx+b中的k与AD解析式的k相同。当直线PN与抛物线仅有一个公共点（即联立直线PN和抛物线解析式，消元后的一元二次方程有二等根，即△=0）时，面积最大，依据△=0，得到直线待定系数b。面积等于△ADN，ND为底，OA为高，面积易求。

参考解答

（4）今日打印题目没有此问，因此粘贴原题解析于此。仅给出方法一的求解过程如下：

注：点击图片可查看高清原图。欢迎分享。

著作权声明

        联系方式： 

        微  信：TheYoungMATH

        Q   Q：497030182 

        T E L：133 3378 5850