用数学告诉你成功的最短路径在哪儿，杨武建的科学成功学第一期

Posted 2021-04-28 杨武建

其实打小我就喜欢数学，不论其他学科怎么样，数学一直保持着名列前茅。只是后来发现社会上不按数学出牌的太多，不讲理性的人太多，甚至是不讲理性的男人也不少（女权主义者请拍砖）。慢慢地让自己学一些商业的东西，开始世故一些，学会社交学会客套。但骨子里自己真不是一个情商太高（当然智商也不高）的人。

     好像有点走题了，我想说成功来着。

    成功有捷径吗？有？没有？相信有捷径的人往下看，不相信有捷径的按左上角的箭头退出（免得说我在安利，在洗脑。。。）

    

    其实捷径是有，但成功是什么大家可能概念不一致。那我们就先研究研究捷径。所谓捷径其实我们计算机专业的同学们都学过：最短路径。就是从起点到终点最短的路。

保持对同一个问题的思考

在那一个瞬间找到了答案

1

人们总是在做一件事情：

找最短路径

公元前32世纪，苏美尔人在粘土片上制作了城市地图，图上描绘了神庙、公园、城墙、河流。这幅地图是世界上现存最古老的地图。随着人类的发展，地图的形式越来越丰富，但其核心都是一致的，也就是帮助人们找到去某个地方的最短路径。

苏美尔人制作的地图是世界上现存最古老的地图

18世纪初，在普鲁士的格尼斯堡，普瑞格尔河从市中心流过，河中心有两座小岛，岛和两岸之间建筑有七座古桥。

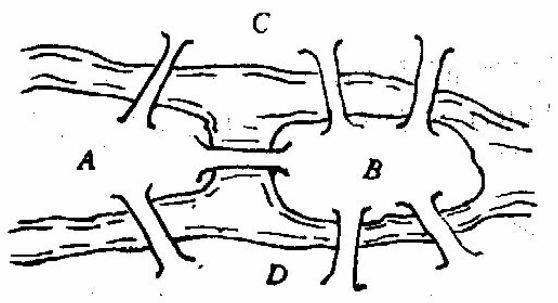
哥尼斯堡的七座桥

当地居民有一项消遣活动，就是试图每座桥恰好走过一遍并回到原出发点。这个问题俗称七桥问题。有很多外地游客慕名而来，跃跃欲试，但从来没人成功过。

于是有人写信给当时著名数学家欧拉，希望他能解决这个问题。欧拉通过简化七桥问题为一个简单图形，证明了这种走法是不存在的。证明过程非常简单，但不经意间他开创了一个新的学科：图论。

时光轮转，20世纪30年代，旅行商问题（Travelling salesman problem， 简称TSP）正式载入史册：

“有一个旅行商人要拜访n个城市，每个城市只能拜访一次，而且最后要回到原来出发的城市。这位商人如何设计拜访顺序，使走过的路径最短？ ”

虽然已经诞生了非常多的启发式算法和精确解法，但一直没有出现能够解决旅行商问题的有效算法。旅行商问题的难度非常大，但是科学家们对它热情不减，希望能找到更加高效的算法。从诞生至今，它一直是优化领域最经常研究的问题之一。

TSP问题历史悠久，最早的描述来自18世纪的骑士环游问题（Knights Moves）

在历史长河中，人们从各个角度致力于寻找最短路径，然而只能做到将路径的表示形式越来越简单，却没有一个机械化算法可以帮助人们快速寻找最短路径。

直到1956年，Dijkstra算法，一个为求最短路径而生的算法，它的诞生改变了这个局面。

2

在咖啡馆诞生的

Dijkstra算法

Dijkstra算法的发明者，叫Edsger Wybe Dijkstra。

故事要从1952年开始说起。当时Dijkstra刚完成学士学位，参加了剑桥大学开设的一个课程。在他的课程导师，也是著名的英国计算机科学家威尔克斯（Maurice Vincent Wilkes）推荐下，Dijkstra来到了荷兰国家数学研究中心（Mathmetical Centre）。在荷兰数学家阿德里安·范韦恩哈登（Aad van Wijngaarden）领导下开始了编程生涯，参与了新计算机的程序研发，包括ARRA I、ARRA II和ARMAC，开始研发荷兰最早期的第一批计算机。

由于这些计算机还在设计当中，Dijkstra的工作实际上是为这些并不存在的机器写程序，而且只能用纸和笔把程序写出来，验证它们的正确性，和负责硬件的同事确认需要的指令是可以被实现的，并写出计算机的规范说明。因此后来他很习惯于不测试自己写的程序，因为无法测试。

时间来到了1956年，Dijkstra从事编程工作到了第4个年头，此时新计算机ARMAC已经研制完成，为了方便向媒体和公众展示ARMAC的计算能力，Dijkstra需要想出一个可以让不懂数学的媒体和公众理解的问题，来验证这台计算机的实力。Dijkstra思考许久，始终没有一个合适的答案。

就在一个阳光明媚的下午，Dijkstra和未婚妻在一家咖啡馆的阳台上喝咖啡，他习惯性地思考这个问题。

而此时Dijkstra的未婚妻并没有察觉呆呆的Dijkstra，一个劲地跟Dijkstra聊起，准备出门去另一座城市拜访贵族的事情。

Dijkstra突然间灵光一闪，如果让计算机演示如何计算荷兰两个城市间的最短路径，这样问题和答案都容易被人理解。

Dijkstra也不管未婚妻的询问，在沐浴在暖和的阳光下，埋头想着自己的问题，终于在20分钟内想出了一个简洁且高效计算最短路径的方法，也就是我们所熟知的Dijkstra算法。

Edsger Wybe Dijkstra

3

Dijkstra算法

是一个既贪心又最优的算法

大名鼎鼎的Dijkstra算法是怎么工作的？

设两个集合，S和U。初始状态下，S只包含源点v，即：S＝{v}，U包含除v外的其他顶点，即：U={其余顶点}。

设dis[u]表示源点v到u的最短距离，若v与U中顶点u有边，则dis[u] = d(v,u)（d(v,u)表示v到u这条边的长度），否则dis[u] = ∞。

第一步，从U中选取一个距离源点v最小的顶点k，即dis[k]最小，把k加入S中，同时在U中剔除k。

第二步，以k为中间点，修改源点v与U中各顶点的距离。若从源点v经过顶点k到顶点u的距离，比原来的dis[u]小（dis[k] + d(k,u) < dis[u]），则更新dis[u]。

第三步，重复第一步和第二步，直至S包含所有顶点，算法结束。

事实上，Dijkstra算法思想非常简洁：

Dijkstra算法对图中的顶点分成两类，一类是已经求出最短路径的顶点集合，用S表示，初始时在S中的只有源点。另一类是其余为未确定最短路径的顶点集合，用U表示。

Dijkstra算法不断在U中挑出与源点距离最短的顶点，加入S中，同时每挑出一个顶点，则利用这个顶点的信息更新U中所有顶点与源点的距离数值。

这种算法有种贪心算法的意味：总是做出在当前看来最好的选择，看似不从整体的角度上考虑，不可能得到最优解。

实际上，Dijkstra算法能够得到最优解，其正确性已被确认，兼具快速和最优的特性。

以Dijkstra算法寻找顶点a与顶点b之间的最短路径

信号传输经过多个节点，必须使用算法计算最短的传输路径

关于成功的捷径欲知后事如何，请听下周分解。。。（下周解不了咱们一起解）