谜之问题：溺水救人的最短路径

Posted 2021-04-28 利维坦

Miss You-Trentemøller 来自利维坦 00:00 07:34

利维坦按：这是一个求极值的问题，有心者不妨用三角函数试着解决这一问题，但这并不是本文最值得讨论的地方。最为神奇的是：无论是光线、狗还是火蚁，都能得出最优解——大自然总能找到最合适的方式。当我们依靠数学工具进行换算的时候，大自然通过进化早已得出了答案。

---

文/Aatish Bhatia

译/Anthony

校对/boomchacha

原文/nautil.us/blog/-to-save-drowning-people-ask-yourself-what-would-light-do

本文基于创作共同协议（BY-NC），由Anthony在利维坦发布

想象一下，你是个救生员，突然看见有人在水中挣扎呼救。一名认真负责的救生员，脑中想的肯定是如何尽快的把ta救上岸来。你虽然是个游泳健将，但在沙滩上奔跑的速度更快。所以对你而言，怎样是到达呼救者的最快的路程呢？这个由著名物理学家理查德·费曼（Richard Feynman）提出的（奇怪的）问题，和光的传播具有一定的相似性。尽管我第一次知道这件事是在10年前，但这个问题与光的行为的相似性给我留下了很深的印象。

图源：Aatish Bhatia

 

你首先考虑到的是直线距离（路程A）是否是最短的。这确实是最短的路程，但并不是最快的。想想看，如果在沙滩上跑的更远，那么陆上路程会增加，水中路程会缩短。但因为你在陆地上奔跑的速度更快，所以在这种情况下，花费的时间可能会更少。

这样的话，也许路程B是最快的？在所有选择中，这条路线游泳的路程最短。但B也不是正确的选择。尽管你跑步速度很快，但是这条路线太长了，同样会增加到达溺水者的时间。

正如你所看到的那样，这个问题中陆上和水中的路程是需要我们去权衡的。正如费曼所说：“代表最短路程的路线中（A）水路过长，而水路最短的路线（B）陆上运动时间又太久，耗时最短的路线一定是这两个因素的合理分配。”实际上，最快的路线是C，很明显这是一条介于路线A和B选择之间的路线。

数学系的学生们会用微积分解决这类最优化问题，但是救生员究竟会怎么做呢？难不成他们会在脑中列出每一种可能，并用公式去计算最优解？我非常怀疑这一点，但我打赌他们最终的选择一定是结合了长期的训练和临场的直觉。正如篮球运动员不需要知道抛物运动原理，就可以投出漂亮的罚球一样。不知怎么的，人不需要进行任何计算，便可以估计出复杂的数学问题（因为一些类似于洋流因素等的变量的介入，实际中用数学方法解决这些问题是更加困难的）。

你可能会问，这究竟与光有何关系？1657年，法国律师和数学家皮埃尔·德·费马【Pierre De Fermat，同样也是费马大定理（Fermat’s Last Theorem）的提出者】，解决了光的传播问题（费马原理的当代解释为：光在运动时，路程的微小变化并不会影响光运动的时间。在大多数情况下，光会选择时间最短的路程。费曼的物理讲义有更多细节）。他证明，当光从一点传播到另一点时，总是会选择耗时最短的路径。这一现象奇妙的暗示着，当救生员想要尽可能快的到达呼救者时，要问自己光会怎么做。

你也可以这么理解，当你用激光笔照向一碗水时，激光也面临着和救生员一样的问题。光会以极快的速度穿过空气，但进入水面后，由于与水分子的碰撞，光的速度会慢下来。这下你看到光会怎样了吧？光会折射，正如救生员到达水域时的运动路径一样。

当你用激光笔向一碗水中发射激光时，你会发现光路出现了弯折，折射角可以通过斯奈尔定律（Snell’s Law）进行计算。图源：Matt Kuchta/CC-BY 

通过斯奈尔定律，你可以准确计算出光线发生偏转的折射角，这一角度与光线穿过的介质，到达分界面时的入射角度有关。虽然公式准确无误，但并不能解释光为何会发生偏折。

费马看待这件事的角度不同。他问道，当光传播的时候，面对那么多条可选的路径，对于任何给定的终点，它会不会总是选择时间花费最少的路程呢？这一现象意味些什么？当得出这一猜想的结论后，他发现这与斯奈尔定律是相符的。费马的猜想完美的印证了所观测到的光的运动。光奇特的行为背后有个合理的解释——一种尚未被发现的方法来解释这一近乎疯狂的现象。

这个发现的意义，远远大于光是如何偏折的。费马的最少时间定理同样解释了光在镜面上对称的反射运动；为什么眼镜是这种形状；为什么卫星天线是锅形的。（你可以从关于费曼的书或者录像中了解这些应用。）

如果你觉得费马的观点有些奇怪，那么放心，你一点也不孤单。费马时期的一个光学领域的著名专家克劳德·克莱尔色列（Claude Clerselier）写下了下面的言论：

费马原理不可能是造成这一现象的原因。这样的话，我们只能把这一现象用自然现象来解释：自然现象的发生并不会有预判，同样自然也不会做出选择，而总是一种带有必然性的果断。

关于费马的观点，大家的困惑在于这一理论似乎需要“能动性”（译注：Agency is the capacity of an actor to act in a given environment. 在哲学里，agency的定义是：对外界或内部刺激、影响作出的反应或回答）的介入。光怎么能选择运动路径？它究竟是怎么知道哪条路径花费时间最短？光是否是通过某种其它的方式，发现了别的路径并非最佳之选。费马当时并不能做出解答。但答案是肯定的，下面是费曼的结论：

最短时间原则，与大自然的因果关系截然相反，与自然规律完全不同。按常理来说，当我们做某件事后，别的事件根据之前的结果尔发生。换句话说，最短时间原则指出，光会发现，选择耗时最短的路线（既最极端的情况）。那么问题来了，光是通过什么方式知道的？光会对每一个选择进行对比嘛？答案是肯定的，是的，从某种角度来说，光是这么做了。

如同“量子擦除”（quantum eraser）等实验所产生的结论——光可以展现出量子的特性，光选择最短路线很难用宏观物理去解释。但是，这些实验，和镜面和抛物面的运用，都是“光确实可以高效地察觉到并选择最短路径”这一观点的有力证据。

最近，我听说了两个关于动物的事。这两个故事中，动物都完成了与救生员拯救溺水者，光的运行路径类似的行为——采用耗时最短的路程从一点到达另一点。至于它们究竟是怎样做到的，仍旧是个谜。

诶尔维斯（Elvis）也许体型很小，但是它却有着很强的计算能力。图源：Tim Pennings

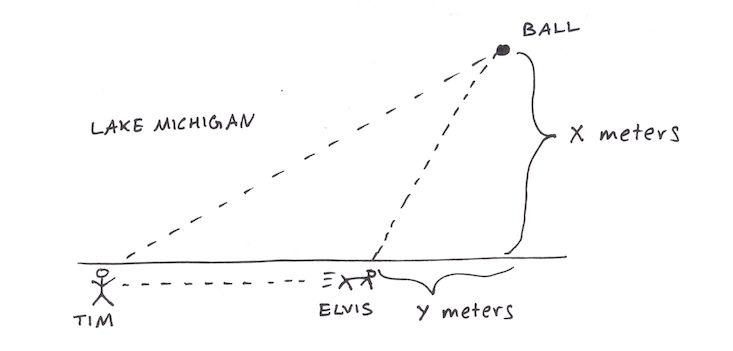
第一个故事是关于一只叫做诶尔维斯的威尔士柯基犬，它的主人是数学教授蒂姆·彭宁斯（Tim Pennings）。蒂姆总是与诶尔维斯在密歇根湖（Lake Michigan）的岸边玩抛接球，他会将诶尔维斯最喜欢的网球扔进水中，诶尔维斯会立即冲出去并将球捡回来。

数学教授蒂姆·彭宁斯和他的爱犬诶尔维斯。图源：The Chronicle of Higher Education

在抛接球游戏中，蒂姆发现诶尔维斯的行为非常有趣。当蒂姆将球扔入水中后，诶尔维斯不会立即跳入水中，游完全程。它并不会选择这样一条看似更加直接的路程。非常明显的，诶尔维斯会先在岸边跑一段，然后到达某一点时，才跳进水中并将球衔回。

蒂姆的脑海中出现了一个问题：诶尔维斯会不会是通过一条耗时最短的路程取回网球的呢？别忘了蒂姆是个数学教授，他很快用微积分解决了问题的最优解。紧接着他决定去验证他的观点。

图源：Aatish Bhatia

蒂姆用了一整天的时间与埃尔维斯在密歇根湖畔玩抛接网球的游戏。他划分出并且测量了诶尔维斯在岸上跑过的距离以及网球运动的距离。在收集了35个数据后（上图中的x和y数值，以米为单位），蒂姆绘制出了这些数据所拟合出的曲线，并用下图的直线画出了代表最优解的直线。

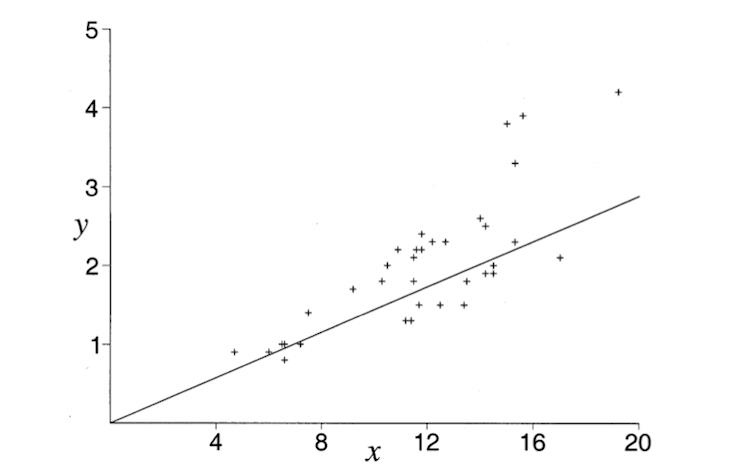
正如蒂姆所预料的那样，诶尔维斯很聪明，总能找到最优路径，既最快而非最短！别忘了，数学模型必须要做出许多假设，让问题简单化，例如：湖没有波浪，水是静止的；诶尔维斯匀速前进，不会因为疲倦尔放慢速度；湖畔可以看作一条直线等等。实际上，诶尔维斯用的时间说不定比数学模型所计算的结果还要短。

图源：Courtney Gibbons/CC BY-NC-SA 3.0

诶尔维斯的举动给蒂姆留下了深刻的印象，他后来写了一篇论文，叫“狗懂微积分么？”。在这论文章中，蒂姆首先消除了读者的疑虑。“诶尔维斯连求微分都不会……实际上，”他紧接着补充道，“它根本不懂微积分。言归正传，虽然它不懂数学，但是诶尔维斯的行为反应了大自然的神奇之处，即自然总会选择最优解。”

【顺便说一下，诶尔维斯并非唯一一个会寻求最优解的犬类。在另外一篇论文中，两个数学家证实，萨尔萨（Salsa），一只雌性的拉布拉多也会选择耗时最短的路径。说不定数学家的狗都会继承主人这方面的潜质呢。】

（www.maa.org/sites/default/files/pdf/mathdl/CMJ/cmj37-1-016-018.pdf）

第二种具有这种奇特能力的生物，是这个世界上最具有侵略性的物种之一——红蚁，既“小火蚁”（Wasmannia auropunctata）。蚂蚁在爬过的路上留下信息素，以此来向同伴传达信息。一段时间之后，信息素会逐渐汇集成一条直线，成为从食物源到达巢穴的最短距离。这些小家伙是这方面的行家，它们甚至可以在比较复杂的迷宫中发现最短路径。之前没有人研究过，当蚂蚁面临着和救生员一样的难题时会怎样。当蚂蚁从较光滑的表面（运动的速度较快）运动至相对较粘的表面（运动速度较为缓慢）上时，它会选择最直接的路径，还是选择花费时间最少的路径呢？

（jeb.biologists.org/content/214/1/50）

一个研究团队开始针对这一问题进行实验。他们用一块玻璃表面以及相对粗糙的绿色桌面来模拟沙滩和海水。他们发现，蚂蚁的选择更加接近于最快，而非直接的路径。正如光的轨迹以及救生员，这些蚂蚁似乎会选择减小时间而非距离。

当蚂蚁从光滑的玻璃表面到达粗糙的绿色桌面时，它们的路径会发生偏转以求更快的到达终点，正如光的运动。图源：Simon Tragust/CC BY 3.0

但是它们究竟是如何做到的呢？总不能真的做数学题吧？研究者表示，很可能是只是运气好罢了。一些蚂蚁碰巧走到了这条更加快速而高效的路上，久而久之，走这条路的蚂蚁越来越多，留下的信息素也越来越多，这条路也就成了首选。但是，没有人真正知道蚂蚁究竟是如何解决了救生员难题。这仍旧是一个开放的问题。

很显然，进化是寻求最优的过程。优胜劣汰，更快更高更强的基因才能留在基因库中。也许我们并不应该惊讶，不同的生物会采用不同的方式而达成相同的结果。所以，下一次被困在车流中，试图找到回家的最快路程，你不妨向蚂蚁、狗和光求教。

往期文章：

---

---

投稿邮箱：[e-mail]

一家过去时的书店

长按上图二维码，或点击“阅读原文”进店