四五个最短路径问题，都用物理方法求解，很有趣！

Posted 2021-04-28 数学教学研究

上一期讲了用等高线的方法在一条直线上寻找一个点，使这个点与位于直线同侧的两个定点连线的夹角达到最大。如下图所示。结果发现，这个点是过两定点的圆弧与直线相切的切点（下图中的点S）。除去这点，直线上的其他点则都是过这两定点的其他圆弧与直线的交点（不是切点），而根据等高线的概念，交点一定不是使某变量（这里是夹角或视角）达到最大值或最小值的点。

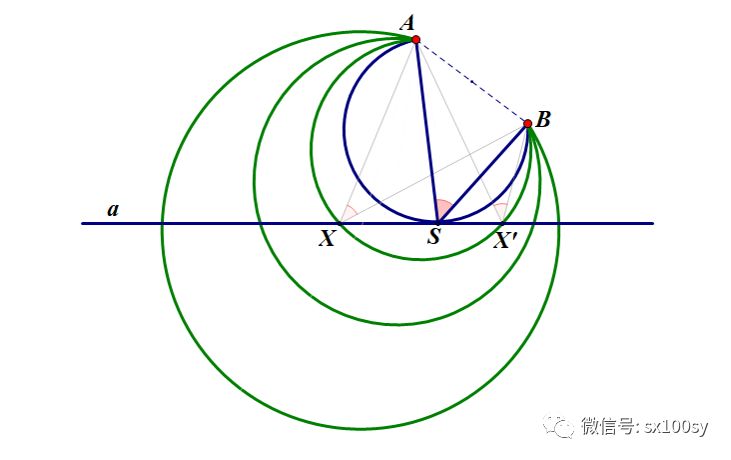
上面的图形中，都是与两定点有关的一系列圆弧，那么，您是否会想到与两定点有关的其他什么图形或曲线？对，椭圆，即到两定点的距离之和等于定长的点的轨迹。

好的，于是，我试着在平面上也画一条直线和位于直线同侧的两个点，再画一系列以这两个定点为焦点的椭圆，如下图所示。其中有一个椭圆比其他椭圆都特殊，即与直线相切的椭圆（图中深蓝色）。

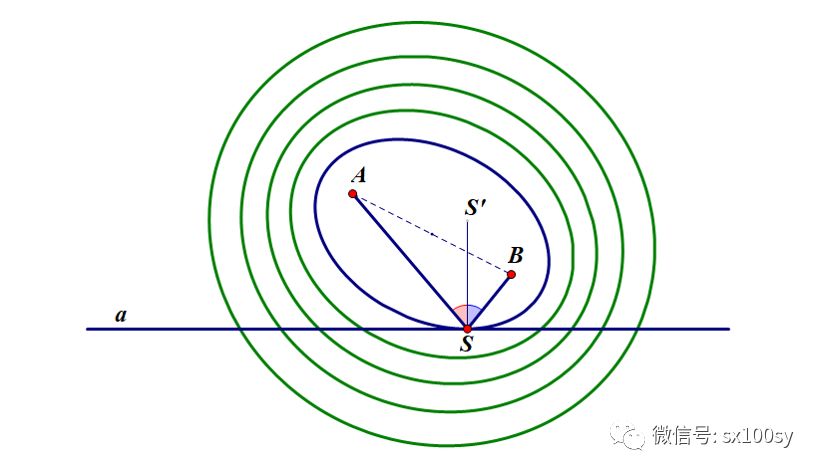
我们上一讲的那个例子是寻找到了最大值点，就是使夹角或视角最大的点，这个点是切点。那么这个椭圆的特殊性特殊在哪里呢？它使什么变量达到最大或最小吗？因为所有这些椭圆的焦点都是相同的两个定点（即同焦点椭圆），所以，我们说这个蓝色椭圆是所画椭圆中最小的一个，这种说法就是有道理的，这个道理就体现在定长2a的大小上，与直线相切的椭圆的2a是最小的。也就是说，一个点在直线上运动，这个切点是使直线上的点到两定点距离之和最小的点。这确实是一个很特殊的点。

其实，求这个点的最简单的办法是，画出一个定点（比如点A）关于直线a的对称点A'，连接点A‘和B，则A'B与直线a的交点就是所求的点S。显然有AS与垂线SS'的夹角等于BS与垂线SS'的夹角。这就是光线的反射定理，即入射角等于反射角，这最早由海伦提出来的。也就是说，假设直线a是一面立着的镜子的截面，点A处有一盏灯亮着，我们位于点B处。若点A与点B之间有东西遮挡着使我们不能直接看到A处的亮灯，但我们可以从镜子中看到这盏灯，我们在镜面上看到的灯的位置就是所求的点S的位置。下图中还显示了，直线a上的其他点到两定点A和B连线之和都大于折线ASB（观察图中绿色线和粉色线。再根据三角形两边之和大于第三边）。

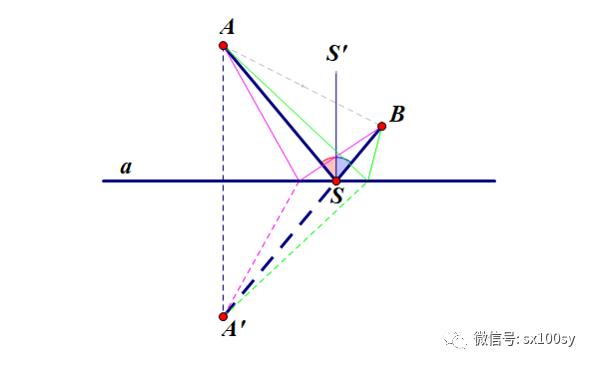
还有两种用物理原理求这个点的方法。第一种方法是，在桌面上固定一根水平直棒，上面套一小圆环，棒与圆环光滑接触，环在棒中可以自由滑动。当然，环不能太大，因为我们还是要认为环是代表一个在棒上运动着的点。取来一根橡皮筋，从环中穿过，把两端分别系在点A和点B处。一定要让橡皮筋拉紧。沿棒左右拖动圆环，但放手后圆环最终都会停留在某个位置，这个位置就是我们所求的点S位置。这时，根据最小势能原理，橡皮筋中张力是最小的（当然是在橡皮筋穿过圆环这一限制条件下）。橡皮筋张力最小，说明长度相对来说已经达到最小。这就等价于路径最短。这个数学问题在现实中的原型有很多，比如直线代表火车线路，A和B是同侧两个村庄，要建一个火车站，火车站与两个村庄之间要修公路。问在哪里建火车站使公路的造价最省。问题基本上可以简化成火车站到两村庄距离之和最小的问题。

另一个物理方法是，在木制黑板上钉两个钉子代表点A和B（两点不在同一铅垂线上）。在黑板上两个钉子的下面用粉笔画一条水平直线a。准备一根适当长度的绳子，一端固定在点B，把点A想像成一个滑轮，把绳子像套在滑轮上一样绕过点A处，要用手握住绳子的自由端。然后在绳子位于两个钉子之间的部分放进一个小圆环（应该是在之前就放进去的，但这个对本问题无关紧要），圆环与绳子之间无摩擦。在圆环上挂一重物。重物是用一根较长的细线吊着的。基本准备好了，我们就用手拉动绳子，同时观察那个小圆环。在小圆环正好与直线a平齐时，把绳子在钉子A处固定好。那么，这时圆环的位置就是我们要求的点S的位置。为什么是这样呢？

我们继续研究。把重物取下。把一支粉笔插入圆环中，然后，移动粉笔，但要求始终让两钉子之间的绳子繃紧。于是，粉笔画出一条曲线。这条曲线一定是椭圆（实际上只能画出半个椭圆，要画出另一半椭圆，需要把两钉子之间的绳子拉到两钉子上面，再画。这是画椭圆的标准方法，也是椭圆的定义）。

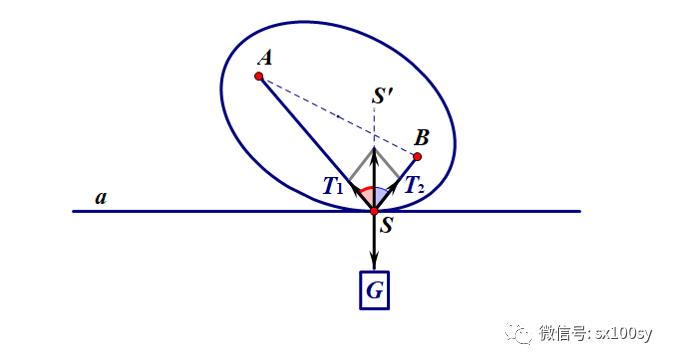
再把重物挂回。根据势能最小原理，重物一定是停留在尽可能低的位置，即椭圆上的其他点都比点S相对于直线来得高。所以，点S一定是椭圆与直线的切点。

另外，小圆环在三个力的共同作用下达到平衡，一个是重物给的向下的拉力G，另外两个是分别指向两个钉子方向的绳子的拉力T1和T2。因为小圆环左右平衡了，所以T1和T2在水平方向上的分力大小相等、方向相反。而T1和T2因为是一根绳子中的张力所以相等（T1和T2在垂直方向上的分力大小相等、方向相同）。所以，T1与铅垂线的夹角等于T2与铅垂线的夹角。这正好对应着光线的入射角等于反射角，也说明，从椭圆一个焦点（比如点A）发出的光，照射到椭圆镜面上，光线一定反射后射向另一个焦点（点B）。

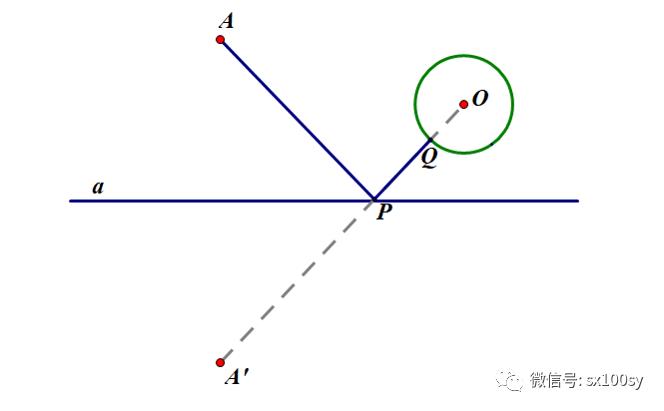
下面是一个简单的拓展问题：也是有一条直线a，在它的同侧有一个定点A和一个定圆O，现在要在定直线a上找一点P，在定圆上也找一点Q，使得点P到定点A的距离AP，与点P到定圆上的点Q的距离PQ，两者之和AP+PQ最小。

这个很简单，如下图所示。同样作点A关于直线a的对称点A'，连接A与圆心O，则A'O与直线a的交点即为所求之点P。A'O与圆的交点即为所求之点Q。用橡皮筋法也可以寻找到点P和点Q。把下图中的圆用一个可以绕圆心旋转的轮子，点P和点Q都用小圆环代替。把橡皮盘筋的一端系在点A处，而另一端先从环P穿过，再系在环Q上。橡皮筋繃紧时，它就是最短路径。

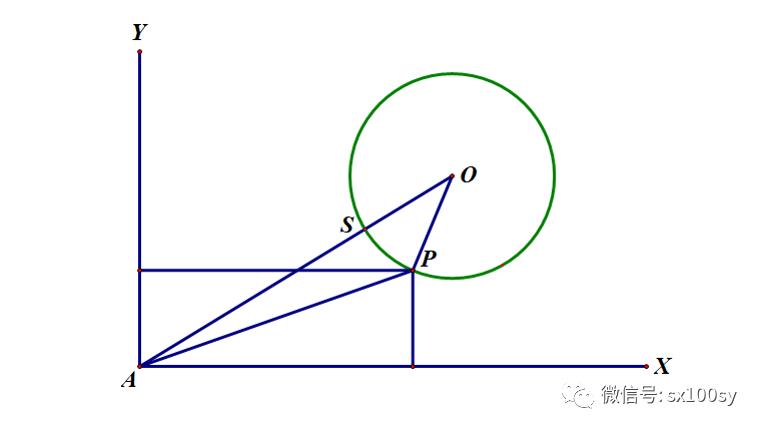
还有很多这样的求最短路径问题，比如：在直角内部有一个圆O，求圆上一点，使得这个点到两直角边的平方和最小。也很简单，解答如下图所示。连接AO，它与圆的交点S即为所求之点。这是因为到两直角边距离的平方和等于这个点到直角点A的距离的平方。所以，就是在圆上找到使AP最小的点P。显然这个点位于连线AO上，即点S。橡皮筋方法很简单，只需把一根橡皮筋一端系在点A，另一端系在套在圆上的小圆环上。圆当然是可以转动的，小圆环也是与圆之间无摩擦，可在圆中自由移动。

下面的问题，相信您一定会解：有一条河（可以近似看成两条平行的直线），在河的两岸之外各有一个村庄（A和B），现在要修一条道路，这条道路是由三条直线段组成的折线，其中的中段是架设在河两岸之间与河岸垂直的桥梁，另两段是分别从村庄到各自岸边的桥端的直线道路。问如何选取桥梁的位置，使三段道路的总长度最短（从而建设费用最省）？答案：从点A向垂直河岸的方向移动河宽的距离到A'，连接A'B，与B所在一边的河岸交于点P，在点P的正对岸取一点Q，于是，PQ就是桥梁的位于，折线AQPB就是所求的最短路径。（也可用橡皮筋模拟：a和b是两根直棒，穿进一个工字型空心管的平行两管当中，中间垂直的圆管两头开洞，然后，把橡皮筋从中间管中穿过，再把两端系在点A和点B上。于是，在橡皮筋拉力的作用下，工字型空心管会沿直线a和b运动，并最终达到平衡位置，这时中间管子的位置就是桥梁的位置。）

今天讲了很多用物理方法解决数学问题的例子，就算是以此纪念伟大的物理学家霍金先生！

好的，下一期给出更多有趣的最小路径问题。