最短路径Dijsktra

Posted 2021-04-28 数据结构C语言版

Dijkstra算法

---

---

---

---

---

---

---

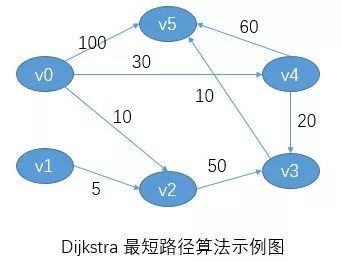
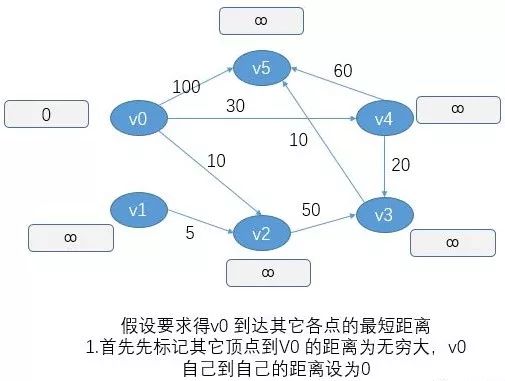
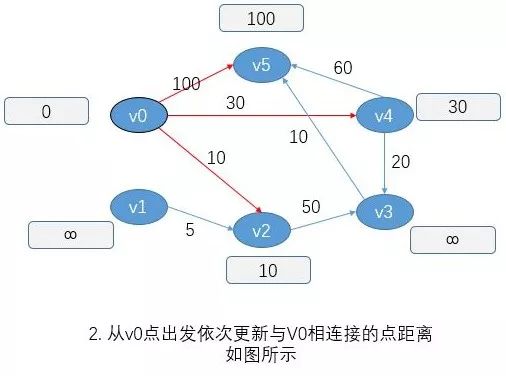
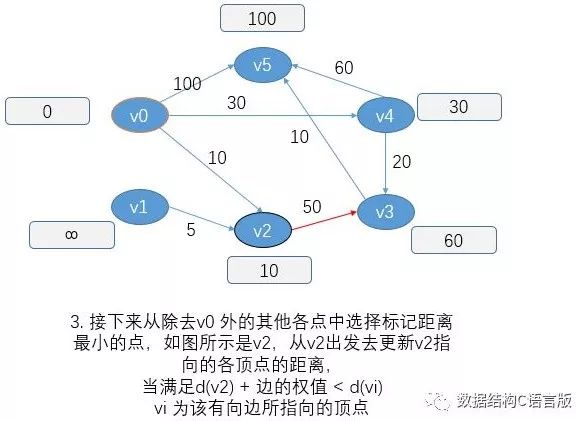
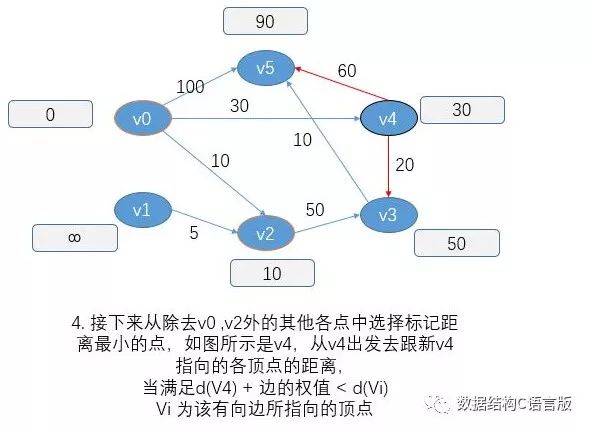
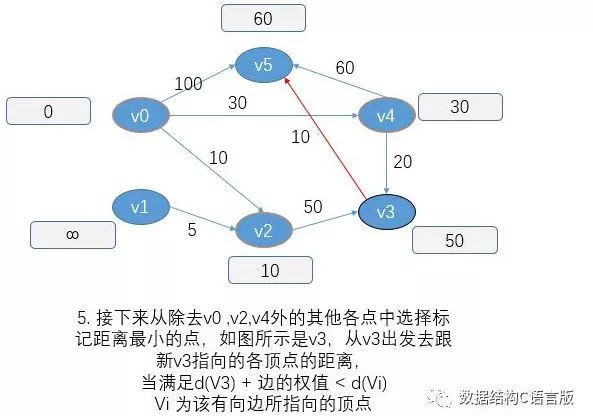
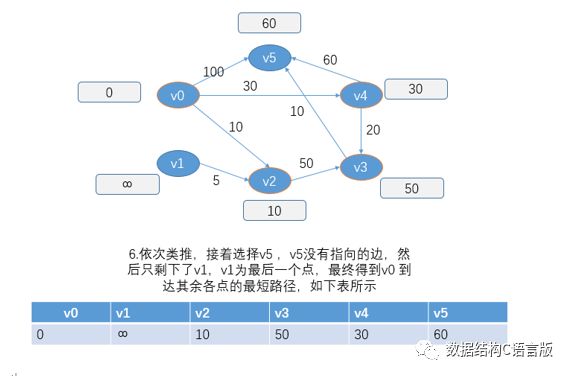
建议在了解算法的基础上 能够更好的理解相关代码

程序：

（程序框可以左右滑动哦~）

/*
    Dijkstra 最短路径算法
*/
#include <stdio.h>
#include <windows.h>
//预定义常量和类型
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define OVERFLOW -2
#define MAX_VERTEX_NUM 20   //最大顶点的个数
#define MAX_EDGE_NUM  30   //最大边的个数
#define INFINITY 65535  //最大值 为int 所能表示的最大值
typedef int Status;
typedef int VertexType;
typedef int VRType;
typedef int InfoType;
// 用于存储最短路径下标的数组
typedef int Patharc[MAX_VERTEX_NUM];
//用于存储到各点最短路径的权值和
typedef int ShortPathTable[MAX_VERTEX_NUM];
//----图的数组（邻接矩阵）存储表示
typedef struct ArcCell{
    VRType adj; //VRType 是顶点关系类型。对于无权图，用0或者1 来表示是否相邻；对带权图，则为权值类型
    InfoType *info; //该弧相关信息指针
}ArcCell,AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
typedef struct{
    VertexType vexs[MAX_VERTEX_NUM];    //顶点向量
    AdjMatrix arcs;     //邻接矩阵
    int vexnum,arcnum;  //图的当前顶点数和弧数
}MGraph;
int LocateVex(MGraph &G,VertexType v)
{
    int i;
    for(i=0;i<G.vexnum;i++)
    {
        if(G.vexs[i] == v)
        {
            break;
        }
    }
    return i;
}
//创建图（邻接链表）
Status CreateGraph(MGraph &G)
{
    //采用数组（邻接矩阵）表示法，构造无向图G
    int i,j,k;
    VertexType v1,v2;
    VRType w;
    printf("请输入图的顶点数和边数\n");
    scanf("%d %d",&G.vexnum,&G.arcnum);
    printf("初始化顶点信息\n");
    for(i=0;i<G.vexnum;i++)
        scanf("%d",&G.vexs[i]);
    //初始化邻接矩阵
    for(i=0;i<G.vexnum;i++)
    {
        for(j=0;j<G.vexnum;j++)
        {
             G.arcs[i][j] = {INFINITY,NULL};
        }
    }
    //构造邻接矩阵
    printf("初始化邻接矩阵信息\n");
    for(k=0;k<G.arcnum;k++)
    {
        scanf("%d %d %d",&v1,&v2,&w);
        i = LocateVex(G,v1);
        j = LocateVex(G,v2);
        G.arcs[i][j].adj = w;
    }
    return OK;
}
/*
    Dijkstra 算法，求有向图G的v0 顶点到其余顶点v 最短路径P[v] 及带权长度D[v]
*/
void ShortestPath_Dijkstra(MGraph G,int v0,Patharc &P,ShortPathTable &D)
{
    int v,w,k,min;
    int final[MAX_VERTEX_NUM]; // final[w] = 1 表示求得点点V0 到Vw 的最短路径
    for(v=0;v<G.vexnum;v++)
    {
        final[v] = FALSE;
        D[v] = G.arcs[v0][v].adj;
        P[v] = 0;
    }
    D[v0] = 0;  //v0 到 v0 的距离为0
    final[v0] = TRUE;   //v0 到 v0 不需要求路径
    //开始主循环，每次求得v0 到某个v 顶点的最短路径
    for(v=1;v<G.vexnum;v++)
    {
        min = INFINITY;
        //当前所知离v0 顶点最近的顶点
        for(w=0;w<G.vexnum;w++)
        {
            if(!final[w] && D[w]<min)
            {
                k = w;
                min = D[w];
            }
        }
        //将目前找到的最近的顶点置为1
        final[k] = TRUE;
        //修正当前最短路径及距离
        for(w=0;w<G.vexnum;w++)
        {
            //如果经过k顶点的路径比现在这条路径长度短的话
            if(!final[w] && (min+G.arcs[k][w].adj < D[w]))
            {
                // 找到了更短的路径
                D[w] = min+G.arcs[k][w].adj;
                P[w] = k;
            }
        }
    }
}
void PrintDistance(MGraph G,int v0,ShortPathTable &D,Patharc &P)
{
    int v,i;
    printf("v0 到 其余各点的距离的为 \n");
    for(v=0;v<G.vexnum;v++)
    {
        i = v;
        printf("(%d,%d) %d \t",v0,i,D[i]);
        if (P[i] == v0)
        {
            if(D[i] == INFINITY)
            {
                printf("\n");
            }else if(D[i] != 0)
            {
                printf("%d<-%d\n",i,P[i]);
            }else
            {
                printf("\n");
            }
        }else
        {
            printf("%d<-",i);
            while(P[i] != v0)
            {
                printf("%d<-",P[i]);
                i = P[i];
            }
            printf("%d\n",v0);
        }
    }
}
int main()
{
    MGraph G;
    int v0 = 0;
    Patharc P;
    ShortPathTable D;
    CreateGraph(G);
    ShortestPath_Dijkstra(G,v0,P,D);
    PrintDistance(G,v0,D,P);
    system("pause");
    return 0;
}

执行结果：