两点之间的最短路径

Posted 2021-04-28 点融黑帮

Hello, 很高兴和大家在这里说算法的事，今天我想分享给大家的是最短路径的取得方式，这种需要大家经常会用到，嗯，比如我在张江高科，现在我要找一家名叫点小融咖啡馆，我还没去过，那么我会拿出百度地图，地图会给我一条最佳(最快)线路。相信这个场景对各位也不陌生，总结出模型，-_-如下:

 

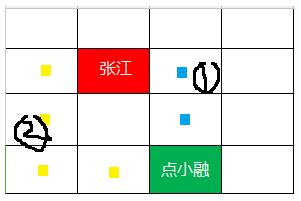
在这个场景里，我们不考虑对角走的情况，就至少有2种的走法，不用多说，大家伙肯定选上面的第1条的，因为近嘛。拿着上面的图，对我们人眼很明显，择最短的一条，问题是机器是不知道的，它会两眼一片黑，不知道这图是干嘛的，除非我们显示的给它这张地图的表示(地图数据)，还有起始点和结束点，它才能有依据得出结论。

既然要表示地图，那我们就用一个数组，一个二维数组表示它，对照上面的图，再看下面的:

 

我们给机器提供一个map的数组，那么机器就有了足够的线索来做事了，无非就是要得到1条从数组里的张江(1)到点小融(2)的路径(可存于另一个数组里)。

现在的问题就是怎么个得到这样一条路径，好像比较麻烦。。。 我们目前在张江这个点上，那么我们先从这个点出发，四周都走一走(先只看水平和竖直方向移动)，我们来看：

 

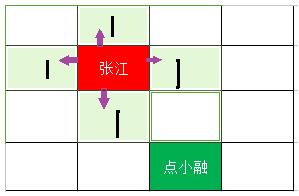
从起点(张江)出发有4个位置可以选择，其实从地图上每个位置往四周看都有4个位置可以走，目前我们就选择上图中张江边上任意画1的方块，继续往未来前进一格，看如下：

 

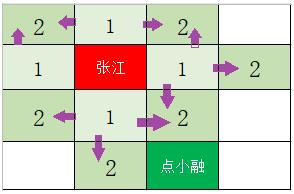
从上面每个画1的地方往四周走，标识了2，每个标识1的地方往四周走地毯式搜了一遍，然后有些标识2的方块离点小融近，有些呢就远了，接下来，再在各标识2的地方再往四周搜一遍看看，就是要标识3的方块了，ok, 我们看看，

 

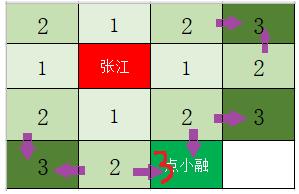
相信眼尖的大家肯定可以看出来了，如上图，我们终于在某个标识3的位置处命中了点小融，到此，找到了终点，我们就可以不用再往四周走了，不用去想着标识4了，因为可以得到一个结果了，

 

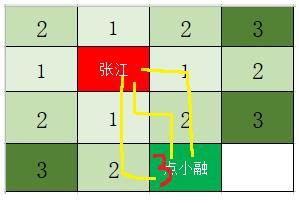
就上面画黄色线条的任意一条都OK,整个过程实质上就是从出发点(张江)开始向外扩散，一圈一圈往外绕，直到在某一圈中命中目标点(点小融)那么整个搜索过程就可以结束了，一条两点之间的最短路径就出来了，哈哈哈，这就是经典的广度优先遍历方法。

接下来我们就来看看代码，任何有趣的东西都离不开枯燥的代码，不过这也没办法，现在计算机还没人工智能到不用输入就能得到任何我们想要的。OK我们来看:

 

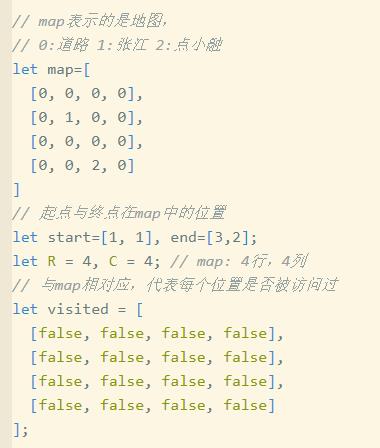
代码里有了队列queue，我们每走一格，都会入队，总的说，起点最先入队，然后标识为1的再入队，接着就是标识2的入队，正是一圈一圈往外扩散，直到某一圈命中目标点，另外一点，就是曾经选过的身边的方块就不用再选了，所以弄了一个visited的变量来记录，最后过程结束了，其中，我从一个方块走到身边的另一个方块，这另一个方块身上我会挂一个prev的变量，指向从哪里过来的，这是为了当我们找到目标点时，可以从目标点身上的prev变量往前回看，回看到最先的出发点，因为只有出发点身上的prev是没有值的，所以path就这样得出了。

最后，希望大家喜欢的话，可以跑一跑上述的过程，用自己喜欢的语言可以写一写，相信大家会有更深刻的体会和感悟。如果有哪里不清楚的，欢迎和我留言，等你来撩哈~~~~

今日推荐