2018年中考数学真题赏析最短路径问题
Posted 中考数学压轴题
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2018年中考数学真题赏析最短路径问题相关的知识,希望对你有一定的参考价值。
唐朝诗人李颀的诗《古从军行》开头两句说:
“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题.
早在古罗马时代,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题.
将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的B地开会,应该怎样走才能使路程最短?
从此,这个被称为“将军饮马”的问题广泛流传.
这个问题的解决并不难,据说海伦略加思索就解决了它.
_____________________________________
中考真题赏析
(2018年黄冈中考数学第13题)
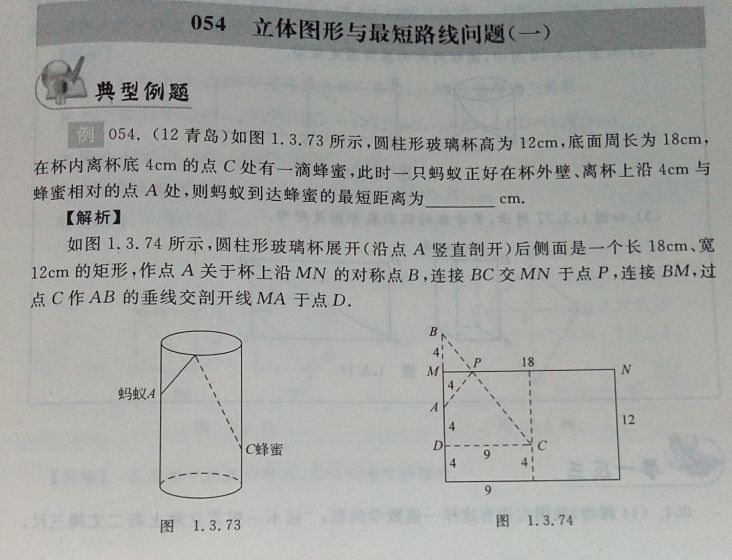
如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为 cm(杯壁厚度不计).
【答案】20.
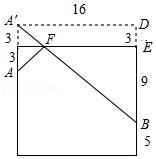
【分析】解:如图:将杯子侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,A′B=√(A′D²+BD²)=20(cm).
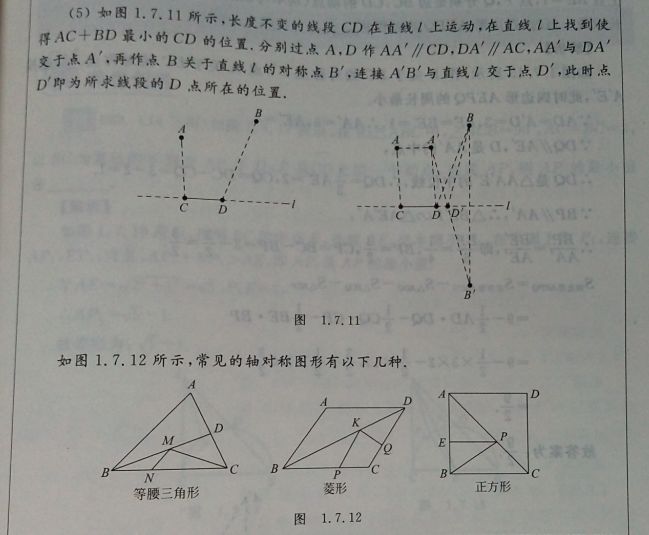
(2018年贵港中考数学第11题)
如图,在菱形ABCD中,AC=6√2,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )
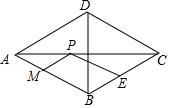
A.6 B.3√3 C.2√6 D.4.5
【答案】C.
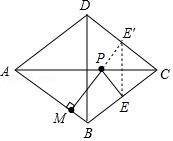
【分析】解:如图,作点E关于AC的对称点E′,过点E′作E′M⊥AB于点M,交AC于点P,则点P、M即为使PE+PM取得最小值,
其PE+PM=PE′+PM=E′M,
∵四边形ABCD是菱形,
∴点E′在CD上,
∵AC=6√2,BD=6,
∴AB=3√3,
由S菱形ABCD=1/2AC•BD=AB•E′M得1/2×6×6=3√3•E′M,
解得:E′M=2√6,
即PE+PM的最小值是2√6.

(2018年滨州中考数学第11题)
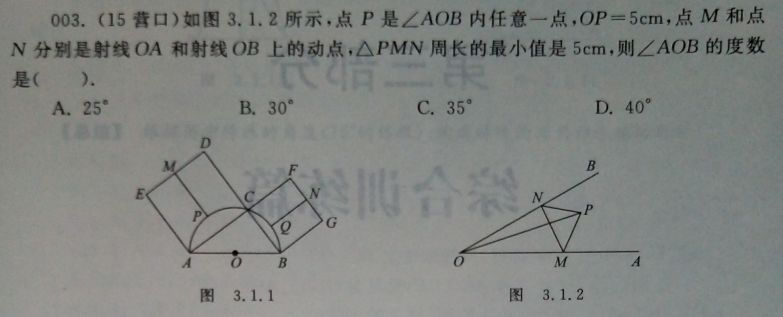
如图,∠AOB=60°,点P是∠AOB内的定点且OP=√3,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )
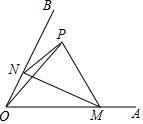
A.3√6/2 B.3√3/2 C.6 D.3
【答案】D.
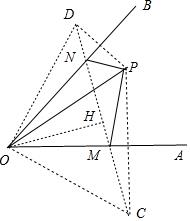
【分析】解:作P点分别关于OA、OB的对称点C、D,连接CD分别交OA、OB于M、N,如图,
则MP=MC,NP=ND,OP=OD=OC=,∠BOP=∠BOD,∠AOP=∠AOC,
∴PN+PM+MN=ND+MN+NC=DC,∠COD=∠BOP+∠BOD+∠AOP+∠AOC=2∠AOB=120°,
∴此时△PMN周长最小,
作OH⊥CD于H,则CH=DH,
∵∠OCH=30°,
∴OH=1/2OC=√3/2,
CH=√3OH=3/2,
∴CD=2CH=3.
(2018年泰安中考数学第12题)
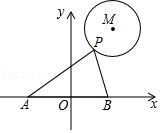
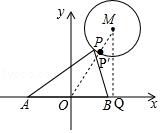
如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A.3 B.4 C.6 D.8
【答案】C.
【分析】解:∵PA⊥PB,∴∠APB=90°,
∵AO=BO,∴AB=2PO,
若要使AB取得最小值,则PO需取得最小值,
连接OM,交⊙M于点P′,当点P位于P′位置时,OP′取得最小值,
过点M作MQ⊥x轴于点Q,
则OQ=3、MQ=4,∴OM=5,又∵MP′=2,∴OP′=3,
∴AB=2OP′=6.
(2018年天津中考数学第11题)
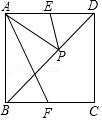
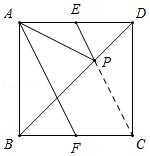
如图,在正方形ABCD中,E,F分别为AD,BC的中点,P为对角线BD上的一个动点,则下列线段的长等于AP+EP最小值的是( )
A.AB B.DE C.BD D.AF
【答案】D.
【分析】解:如图,连接CP,
由AD=CD,∠ADP=∠CDP=45°,DP=DP,可得△ADP≌△CDP,
∴AP=CP,
∴AP+PE=CP+PE,
∴当点E,P,C在同一直线上时,AP+PE的最小值为CE长,
此时,由AB=CD,∠ABF=∠CDE,BF=DE,可得△ABF≌△CDE,
∴AF=CE,
∴AP+EP最小值等于线段AF的长.
(2018年新疆中考数学第9题)
如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是( )
A.1/2 B.1 C.√2 D.2
【答案】B.
【分析】解:如图,作点M关于AC的对称点M′,连接M′N交AC于P,此时MP+NP有最小值,最小值为M′N的长.
∵菱形ABCD关于AC对称,M是AB边上的中点,∴M′是AD的中点,
又∵N是BC边上的中点,∴AM′∥BN,AM′=BN,
∴四边形ABNM′是平行四边形,∴M′N=AB=1,
∴MP+NP=M′N=1,即MP+NP的最小值为1.
以上是关于2018年中考数学真题赏析最短路径问题的主要内容,如果未能解决你的问题,请参考以下文章