最短路径-4

Posted 2021-04-28 初中数学题解视频

最短路径-4

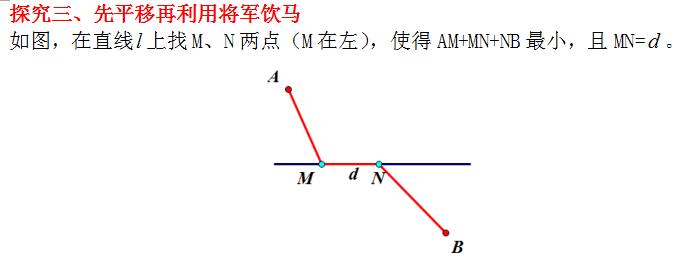
【分析】AM+MN+NB最小，也就是说只需要AM+NB最小即可。我们会想到两点之间线段最短这个知识点，但是点M和点N不是同一个点，问题就不那么简单，不过我们可以借助“转化”的思想，通过平移把点M和点N移动到“同一个点”从而达到解决问题的目的。

接下来我通过作图演示一下

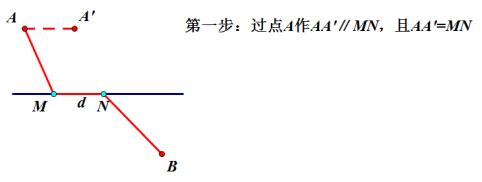
动态演示

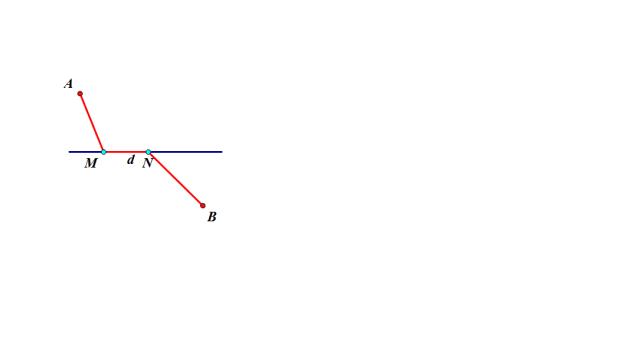
【例】（2013•鄂尔多斯）如图，A和B两地在一条河的两岸，现要在河上造一座桥MN，使从A到B的路径AMNB最短的是（假定河的两岸是平行直线，桥要与河岸垂直）（　　）

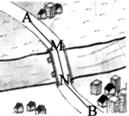
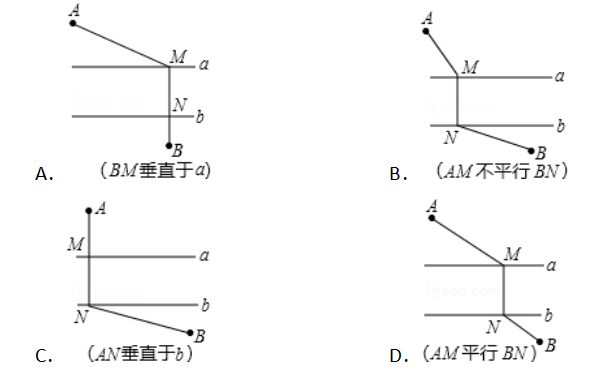
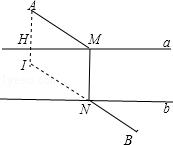
【解答】解：根据垂线段最短，得出MN是河的宽时，MN最短，即MN⊥直线a（或直线b），只要AM+BN最短就行，即过A作河岸a的垂线AH，垂足为H，在直线AH上取点I，使AI等于河宽．连结IB交河的b边岸于N，作MN垂直于河岸交a边的岸于M点，所得MN即为所求．

故选：D．

问题1：如果点A和点B在同侧时，AM+MN+NB最小，此时问题该怎么解决呢？

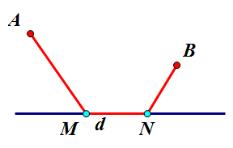
【分析】借助上面的探究我们已经知道要想把点M和点N变为同一个点需要通过平移解决问题，当平移过后我们发现点A和点B在直线的同侧，刚好符合“两定一动一直线”模型，那么问题就好办了。

动态演示

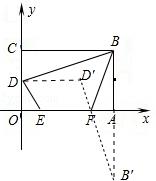
【例】在平面直角坐标系中，矩形OABC如图所示．点A在x轴正半轴上，点C在y轴正半轴上，且OA=6，OC=4，D为OC中点，点E、F在线段OA上，点E在点F左侧，EF=3．当四边形BDEF的周长最小时，点E的坐标是（　　）

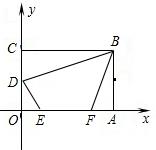
令y=0，得﹣2x+8=0，解得x=4，

∴F（4，0），E（1，0）．

【例】（2010天津市中考）在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，OA=3，OB=4，D为边OB的中点．

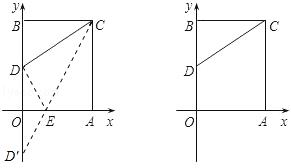
（1）若E为边OA上的一个动点，当△CDE的周长最小时，求点E的坐标；

（2）若E、F为边OA上的两个动点，且EF=2，当四边形CDEF的周长最小时，求点E、F的坐标．

（温馨提示：可以作点D关于x轴的对称点D′，连接CD′与x轴交于点E，此时△CDE的周长是最小的．这样，你只需求出OE的长，就可以确定点E的坐标了．）

【分析】（1）由于C、D是定点，则CD是定值，如果△CDE的周长最小，即DE+CE有最小值．为此，作点D关于x轴的对称点D′，当点E在线段CD′上时，△CDE的周长最小；

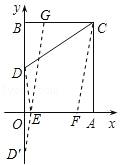
（2）由于DC、EF的长为定值，如果四边形CDEF的周长最小，即DE+FC有最小值．为此，作点D关于x轴的对称点D′，在CB边上截取CG=2，当点E在线段D′G上时，四边形CDEF的周长最小．

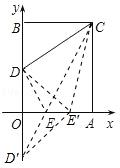
【解答】解：（1）如图，作点D关于x轴的对称点D′，连接CD′与x轴交于点E，连接DE．

若在边OA上任取点E′与点E不重合，连接CE′、DE′、D′E′

由DE′+CE′=D′E′+CE′＞CD′=D′E+CE=DE+CE，

可知△CDE的周长最小．

∵在矩形OACB中，OA=3，OB=4，D为OB的中点，

∴BC=3，D′O=DO=2，D′B=6，

∵OE∥BC，

   

【练习】已知点A（3，4），点B（﹣1，1），在x轴上有两动点E、F，且EF=1，线段EF在x轴上平移，当四边形ABEF的周长取得最小值时，点E的坐标为　　．

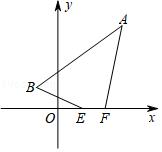
【分析】欲使四边形ABEF的周长最小，由于线段AB与EF是定长，所以只需BE+AF最小．为此，先确定点E、F的位置：过点A作x轴的平行线，并且在这条平行线上截取线段AA′，使AA′=1，作点B关于x轴的对称点B′，连接A′B′，交x轴于点E，在x轴上截取线段EF=1，则点E、F的位置确定．再根据待定系数法求出直线A′B′的解析式，然后令y=0，即可求出点E的横坐标，进而得出点E的坐标．

【解答】解：如图2，过点A作x轴的平行线，并且在这条平行线上截取线段AA′，使AA′=1，作点B关于x轴的对称点B′，连接A′B′，交x轴于点E，在x轴上截取线段EF=1，则此时四边形ABEF的周长最小．

∵A（3，4），∴A′（2，4），

∵B（﹣1，1），∴B′（﹣1，﹣1）．

设直线A′B′的解析式为y=kx+b，

【练习2】已知平面直角坐标系中A、B两点坐标如图，若PQ是一条在x轴上活动的线段，且PQ=1，求当BP+PQ+QA最小时，点Q的坐标　　．

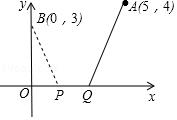
【分析】如图把点B向右平移1个单位得到E（1，3），作点E关于x轴的对称点F（1，﹣3），连接AF，AF与x轴的交点即为点Q，此时BP+PQ+QA的值最小．求出直线AF的解析式，即可解决问题．

【解答】解：如图把点B向右平移1个单位得到E（1，3），作点E关于x轴的对称点F（1，﹣3），连接AF，AF与x轴的交点即为点Q，此时BP+PQ+QA的值最小．

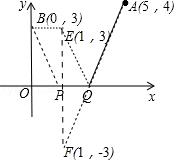
问题2.当MN由水平方向变为竖直方向时，如何求解AM+MN+NB的最小值，相比问题1，作图方法发生变化了吗？

、

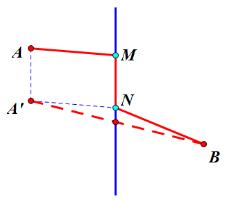
当MN变为竖直方向的时候，点A平移方向也发生了变化，这样做的目的是让四边形AA’NM为平行四边形。最终得到AM+MN+NB的最小值为A’B+d。

【分析】MN表示直线a与直线b之间的距离，是定值，只要满足AM+NB的值最小即可．过A作直线a的垂线，并在此垂线上取点A′，使得AA′=MN，连接A'B，则A'B与直线b的交点即为N，过N作MN⊥a于点M．则A'B为所求，利用勾股定理可求得其值．

【解答】解：过A作直线a的垂线，并在此垂线上取点A′，使得AA′=4，连接A′B，与直线b交于点N，过M作直线a的垂线，交直线a于点N，连接AN，过点B作BE⊥AA′，交射线AA′于点E，如图．

∵AA′⊥a，MN⊥a，

∴AA′∥MN．

又∵AA′=MN=4，

∴四边形AA′NM是平行四边形，

∴AM=A′N．

由于AM+MN+NB要最小，且MN固定为4，所以AM+NB最小．

由两点之间线段最短，可知AM+NB的最小值为A′B．

THE END

最短路径大结局.