模块化立面设计

Posted 2021-04-27 FKingAwesomeArchitects

模块化立面设计是一公司李迅涛李总提出的一种创新型设计方法。其大意是将立面分段作为集中标准化模块，通过对模块的拼接组合来完成立面设计。这样的设计方法既可以节约设计时间也可帮开发商降低成本。

 

以某项目的沿江商业为例如（图1）沿江商业截取段所示：

图1：某项目沿江商业截取段

从上图所示该段商业的主要组成模块有5种如下图（图2）所示：

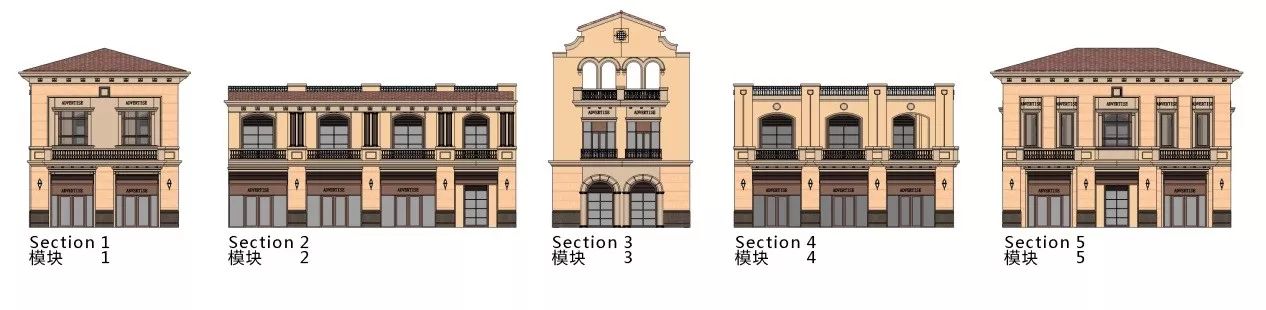
图2：某项目沿江商业5种模块化标准段

该沿江商业则是用这5种模块化标准段，不重复拼接组合得出。

 

上述项目的设计过程为：首先用Sketchup先行设计好标准段，再用人工手动的方式拼接的方式来完成立面模块的拼接，最后通过几种方案对比，设计师主观选择出最优的设计。但这种手动排列组合的方式有一定的局限性。例如立面模块为5段，如果采用5种模块不重复排列组合，则有50种排列方式；若是5种模块的可重复排列组合，则有3125种排列方式。因为排列组合的方式太多，设计师在相对有限的设计时间内能尝试的拼接方式有限，并不能涵盖全部。那么如何让该手法更加灵活的运用，且能辅助设计师得出更多可能的排列方法。下面笔者将借助参数化软件，做一些尝试。

 

本研究主要分为两大块，第一步是采用Grasshopper辅助做理论上的模拟，若理论成立，再导入模型做实际操作的尝试。首先，在犀牛中设置A、B、C、D四个Box，作为代替立面模型的基本研究模块（图3），并通过高度来区分四模块。

图3：基本模块

 该四个模块每一个都有四种不同的排列组合方式如下（图4）所示。

  

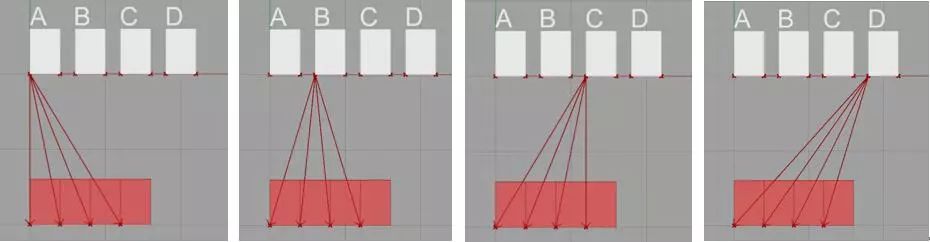
图4：基本模块的排列组合方式

若采用4种模块的不重复排列方式，则有24种排列方法。若采用可重复排列组合方式则有256种排列组合方式。本研究先针对稍微简单的不重复排列组合方式做尝试。借助参数化软件Grasshopper编程制作出4的无重排列组合组件（图5），此组建是基于最简单的排列组合公式C（n，r）。组建的制作尽量简单，并用Box代替立面标准段，这样可减少电脑的运算量。最后通过分组排列，列举得出4个Box的无重排列组合的24种结果。

图5：无重排列组合组件

接下来将4种基本模块与组件连接，如（图6）与（图7）所示所示，得出24种无重排列结果，通过对slider滑动器对参数的调整，可以看到不同的拼接组合方式。

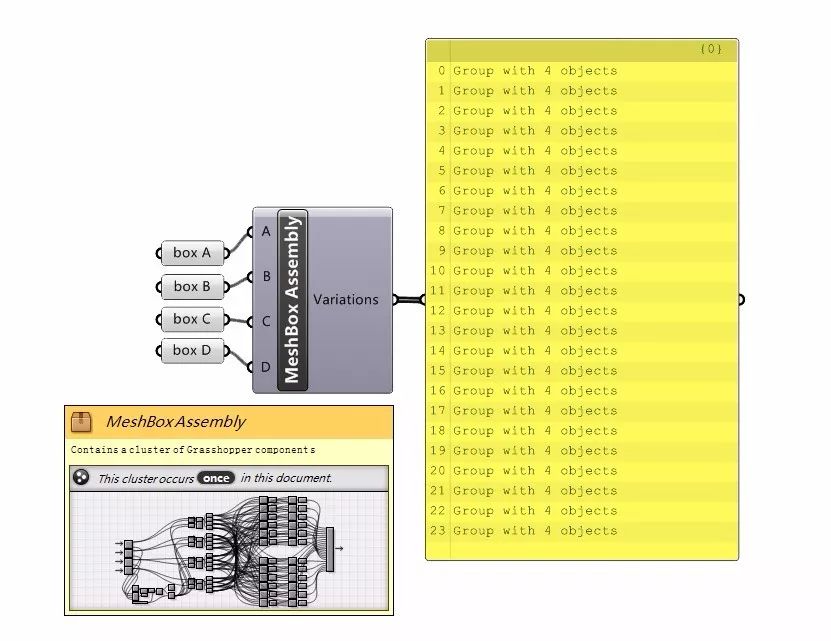
图6：运算结果展示

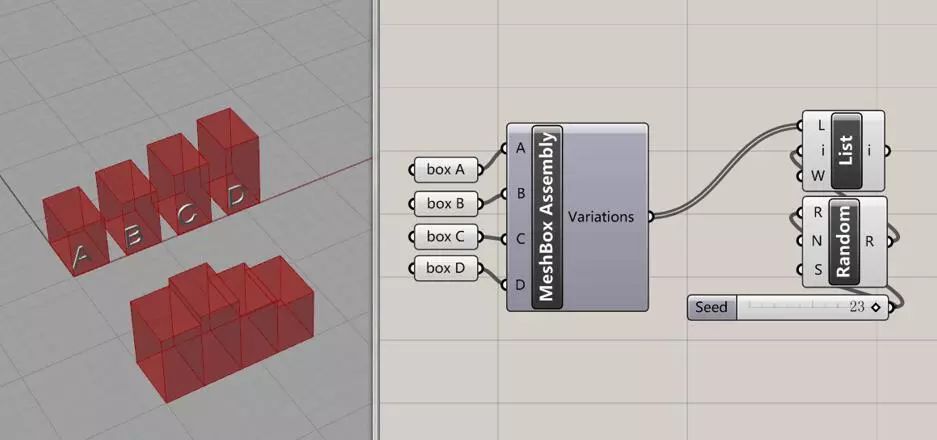
图7：动图演示

通过上述测试，证明4种基本模块的无重排列理论上是可行的。

 

接下来，需将实际导入模型进行测试，探索在实际操作中该理论能得出什么样的结果。如下图8所示，A、B、C、D四个立面是选定作为基准单元的立面模块。将模型在犀牛模型空间里转换为Mesh，再导入Grasshopper。通过Bounding Box将模型限定成盒子。通过这样的方法赋予立面模型一定的属性，与之前研究过程中选用Box作为研究对象相符。

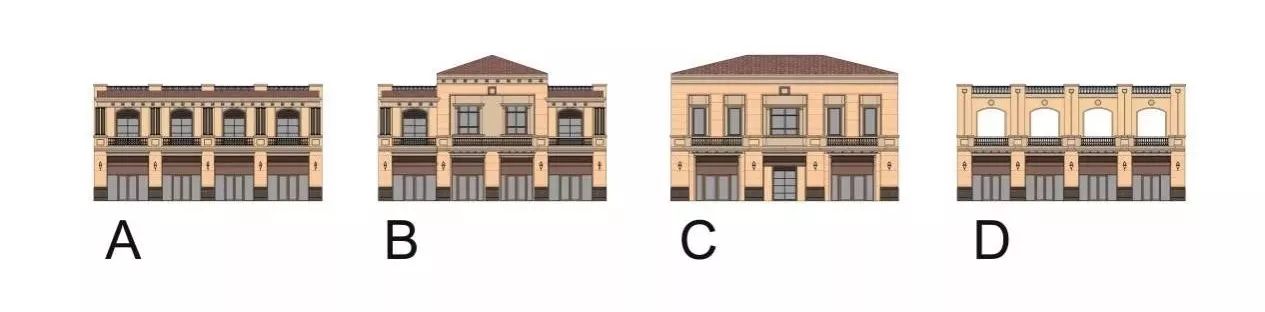
图8：立面模块基准单元

准备工作完毕后，将有属性的Box连接到无重排列组件（图5）上，如下图9所示，左侧立面组合可随着右侧slider滑动器参数的变化而变化。图10便是24种不同的立面排列组合的结果。

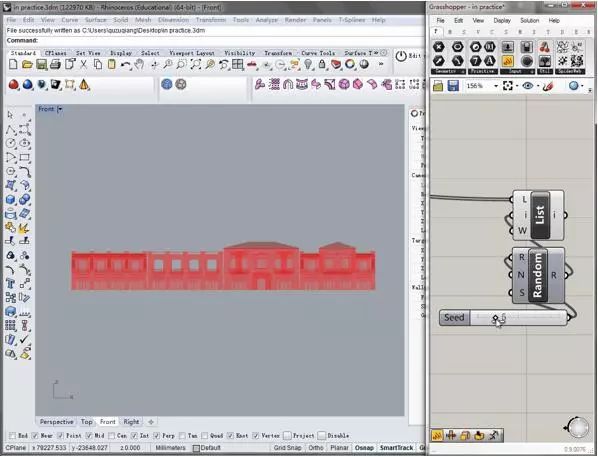
图9：立面模块排列方式演示

 

图10：成果展示

以上部分所研究的4种基本模块的无重排列，证明是实际可行的。并可以运用于实际项目中。设计师只需要通过设计完成基本模块，并将之导入Grasshopper连接到组建上，便可得出所有结果，设计师只需从结果中选择出最优组合即可。但如果要进行对可重复排列组合方式的研究，需要通过程序语言结合排列组合公式（图11）编译出新的组件再进行测试。

图11：排列组合公式

 

本文所介绍的只是该研究第一阶段的研究成果，接下来还会有后续的研究，希望未来的立面设计可通过参数化软件的辅助，运用模块化排列组合来进行。目前该研究还处于初步阶段，如各位有好的想法，敬请指正。