基于图数据的数据挖掘及相关算法介绍
Posted 新蜂数字金融
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于图数据的数据挖掘及相关算法介绍相关的知识,希望对你有一定的参考价值。
“人的本质不是单个人所固有的抽象物,在其现实性上,它是一切社会关系的总和。”
—《马克思恩格斯选集》
第一,人作为社会关系的总和而产生;第二,作为一切社会关系的总和而存在和发展;第三,人的本质的具体性、历史性。中学政治课本上的马克思和恩格斯早已告诉我们只有从分析社会关系出发结合其随着时间上的变化,才能科学地认识人的本质,才能真正弄清人的本质发展的客观规律性。
而目前传统的营销、风控等各类模型主要依赖从关系型数据库中挖掘反应客户固有属性如资产、负债、消费、年龄等数据来进行相关训练,要想挖掘出反应客户社会关系的社交型数据或者客户的时序变化数据(关系型仅能取到如资产变化率这类的简单数据),就需要依托新一代的图数据库。
关系型数据库的局限性
传统的关系型数据库通过实体和关系来建模,但在处理非常复杂的实体关系时,关系型数据库往往变得力不从心。当我们要表示实体间的多对多关系时,一般会建立关系表,当要看实体间的关系时,需要把这种关系再关联起来,特别是在处理关系非常复杂或者关系层次很多的情况下,需要关联很多的表,甚至产生非常巨大的中间结果,导致查询非常缓慢甚至跑不出来。如依靠关系型数据库实现的套现模型,不论业务规则和定义的区别有多大,模型实现的方法仍离不开对于流水表的反复关联,而受限于关系型数据库关联方式导致的效率问题,仅3-4层的单链路关联已然无法对稍微有金融反侦察意识套现客群的锁定。
图数据库的优势
图数据库以图论为基础,数据本身以图的方式存储,对于外在的用户来说,各个实体就是各个点,而点与点之间的边代表了实体间的各类关系,如股权,资金流,担保,父子等,实体的属性挂在点上,关系的属性挂在边上。该实现方式使得图数据库在处理知识图谱、社交网络分析、反欺诈、反套现等依托实体间关系建模类型的应用时有着先天的优势。图数据库可以方便的回答类似于:和用户以某类关系关联的用户有哪些,两个间接关联的用户之间相距多远(距离取决于具体的业务定义);用户和用户之间的关联网络有什么样的特征等问题。如经典的反欺诈模型可以在图中分三步更加有效的运行分析特定用户可以通过什么样的关系关联在一起:
1、通过特定的规则筛选可疑似用户
2、查看与可疑用户有特定关联的用户
3、查看与可疑用户有特定关联的所有用户组成的子网的网络特征及用户特征
目前最新一代的图数据库Tigergraph依托其强大的分布式架构已经实现每秒遍历上亿个顶点/边,并遍历三到十步以上,使得反欺诈模型在真正意义上具备了实时深度链接分析的可能性。
当然这也并不意味着传统的数据库的没落,图数据擅长是特征网络分析,而传统的关系型数据库更擅长的是特征指标分析。因此采用图数据库+关系型数据库+机器学习相结合的模式,即从图数据库从提取关于个人的社交关系类指标后结构化变化存储至传统的数据库中和已有的特征指标共同作为机器学习中的自变量进行相关联合建模可能是未来的一种常见方式。
总而言之,图数据库的到来可以使得对某人的数据分析变成对处于某个时序变化中某个圈子中某人的数据分析,实现了从单点到网络,从静态到动态的转变,提升了对客户认知的全面性。图数据库的优势来源主要是其点边实现的结构使得图论中丰富的算法可以被应用到数据挖掘中,这些算法的应用使得图数据库可以挖掘出远超传统关系型数据库的复杂网络特征,从而为后续的机器学习提供更加多样化的素材支持。目前成熟的图数据库算法主要分三大类:
1、Path:该类算法主要用于计算节点之间最短路径;
2、 Centrality:该算算法主要用于量化网络中节点的重要程度;
3、 Community:该类算法主要用于社交网络中子网的划分;
当前新一代的图数据库TigerGraph中算法仅依托于普通的Query便可实现,这种方式极大的方便了使用者根据特定的业务场景进行算法的定制化开发,前提是使用者对于图数据库中经典算法的原理和步骤有一定了解,下面在各类算法种选取几种经典算法进行介绍:

1 、Path
主流的Path算法包括Dijkstra、Bellman_Ford、SPFA等;Disjkstra时间复杂度为O(VlogV)(本文默认V为点数,E为边数),快于Bellman_Ford和SPFA的O(VE),但Disjkstra无法适用于存在负权路径的图中;Bellman_Ford适用于存在负权路径中,前提是不存在负权回路;SPFA可以看成是Bellman-ford的队列优化版本,但在图很稠密的时候时间差不多。
1.1 Dijkstra
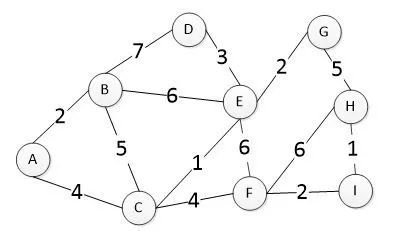
如上图所示,Dijkstra算法本质是通过一种贪心的策略来计算出A图中每一个其他顶点的距离,其声明一个数组distance来保存A到各个顶点的最短距离和一个保存已经找到最短路径的顶点的集合T,以下是一个算法的执行示例:
第一步:T={A},因此从T出发找到的distance数组为:

第二步:从distance数据中找到除T集合中点以外当前最短路径最短的点加入到集合T中,此时集合T={A,B},且数组中A到B的距离已经从当前最短路径变成了最终最短路径(因为A通过任何其他节点连到B的路径肯定大于A到该节点的最短路径大于A 到B 的最短路径)。因此A从B连接到的别的节点的最短距离=B到别的节点的最短距离+AB之间的最短距离2,使用T={A,B}中新加入的点B来更新最短路径数组distance,ABD=AB+BD=9,ABE=AB+BE=8,ABC=AB+BC=7,之后使用新计算出来的路径和原来数组中存在的最短路径比较,取两者之间小的值作为新的当前最短路径。
因此从T={A,B}出发更新distance数组为:

第三步:从distance数据中找到当前最短路径最短的店加入到集合T中,此时集合T={A,B,C},且A到B、C的距离已经从当前最短路径变成了最终最短路径,同上计算出通过节点C更新的distance数组为:

类似的,第四步T={A,B,C,E},distance数组更新为:

这样每一步可以确定A到其中一个点的最终最短距离,最终T={A,B,C,E,G,F,D,I,H},确定最短路径的顺序依次为B(2)>C(4)>E(5)>G(7)>D(8)>F(8) >I(10)>H(11), distance数组更新为:

1.2 Bellman_Ford
Bellman_Ford算法的时间复杂度比Dijkstra高,但可以解决Dijkstra无法解决的存在负权值边图(没有负权回路,该类状况无解)的最短路径问题,不同于从点考虑的Dijkstra算法,Bellman_Ford主要是从边的角度进行考虑,用一句话概括Bellman_Ford算法的就是:对所有的边进行n-1次松弛操作。如果图中存在最短路径(没有负权回路),那么最短路径包含的边最多为n-1条,以下是一个算法的执行示例:
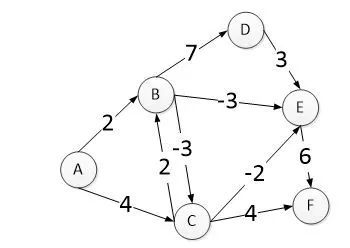
第一步,类似于Dijksra算法建立一个当前最短路径数组distance,区别在于Dijksra算法每一次循环会确定一个最短路径的点,但是Bellman_Ford仅知道有一个点已经是最短路径,但却无法判断具体的点,因此不能像Dijksra算法那样只找该点的边进行下一步计算,而是需要遍历所有的边进行循环,这也是Dijksra算法时间复杂度为O(VlogV),而Bellman_Ford时间复杂度为O(VE)的最本质原因。如上图建立的distance数组为:

第一次循环所有边,判断是否使得distance数据发生变化。
对于边AB:
A-A-B=distance[A]+AB=2=distance[B],不更新distance;
对于边AC:
A-A-C=distance[A]+AC=4=distance[C],不更新distance;
对于边BC:
A-B-C=distance[B]+BC=-1<distance[C]=4,distance更新

对于边BD,A-B-D=distance[B]+BD=9<distinct[D]=∞, distance更新为

对于边BE,A-B-E=distance[B]+BE=5< distinct[E]=∞, distance更新为

对于边CB,A-C-B=distance[C]+CB=6>distance[B]=2,不更新;对于边CE,A-C-E=distance[C]+CE=-3<distance[E]=5,distance更新为

对于边CF,A-C-F=distance[C]+CF=3>distance[F]=∞,distance更新为

对于边DE,A-D-E=distance[D]+DE=∞,不更新
对于边EF,A-E-F=distance[E]+EF=3,distance更新为

循环执行以上操作V-1次即得到最终的结果。
特别注意对于存在负权值的图若存在负权回路的情况下是不存在最短路径的,因为每次走一圈负权路径都会使得距离变短。因此我们在通过V-1次循环所有边完成计算后,需要再次对distance数组作最后一次遍历循环所有边,如果distance数组被修改,说明存在有负权回路,此时图不存在最短路径,返回false;如果distance数组未被修改,那么distance数组即为最终的最短路径结果。

1.3 SPFA
SPFA可以看成是Bellman_Ford的队列优化版本,正如前面讲到的,Bellman_Ford每一轮用所有边来进行松弛操作可以多确定一个点的最短路径(尽管不知道是哪个具体的点),但是用每次都把所有边拿来松弛太浪费了,不难发现,只有那些已经确定了最短路径的点所连出去的边才是有效的,因为新确定的点一定要先通过已知(最短路径的)节点。所以我们只需要把已知节点连出去的边用来松弛就行了,但是问题是我们并不知道哪些点是已知节点,不过我们可以放宽一下条件,找出可能是已知节点的点,也就是之前松弛后更新的点,已知节点必然在这些点中。在效率上,当图很稠密的时候spfa就退化成和Bellman-Ford差不多了,因为对于入队的每个节点都要和很多节点去进行松弛操作。

2 、Centrality
中心性算法的作用是量化网络中顶点的重要性,图中节点的重要性判断根据不同的应用场景会有区别,因此实际应用中常采用多种算法如Dgree,Closeness,Betweenness,Pagerank等相结合从各个角度进行综合量化;时间复杂度方面,由于Degree仅需统计节点相关的边数,因此耗时仅为O(1),Closeness和Betweenness算法由于需要计算该节点到其它所有节点间的最短路径,因此其取决于调用的最短路径算法的时间复杂度,无负权值边时为O(VlogV),有负权值边时为O(VE),Pankrank的每次迭代计算会涉及到整个图,因此其时间复杂度为O(EK)(K为收敛迭代的次数,一般可以通过手动设置最大迭代次数,或者设定一个最小变动阈值)。
2.1 Degree
Degree算法主要是通过度(连接该点的边)来量化节点的重要性。设想一下,微信中有50个好友的A一般比仅有20个好友的B社交圈子广,认识的人多。当然,刚才这个情况是无向图的情形,如果是有向图,需要考虑的出度和入度的问题,如在微博等社交场合,你关注的人和关注你的人是应该分开考量的,这反映到图上就是有向图的出度和入度问题。同时如果不同社交场合之间要是想用统一的标准来衡量的话,还需要考虑每个社交关系所对应图的规模大小,即去规模化问题。
2.2 Closeness
Closeness算法考量的是节点到其他所有节点的最短路径,最短路径类的算法在本文之前的部分已经作了相关介绍,接下来设想一个实际生活中的场景,比如你要建一个大型的娱乐商场,你可能会希望周围的顾客到达这个商场的距离都尽可能地短。这个就涉及到接近中心性的概念,接近中心性的值为路径长度的倒数。接近中心性需要考量每个结点到其它结点的最短路径的平均长度。也就是说,对于一个结点而言,它距离其它结点越近,那么它的中心度越高。一般来说,那种需要让尽可能多的人使用的设施,它的接近中心度一般是比较高的。
2.3 Betweenness
Betweenness算法考量的是节点作为其他两个节点间最短路径的桥梁作用。想象一下我们身边总有那么一些社交达人充当着介绍A认识B的角色。Closeness通过量化一个结点担任其它两个结点之间最短路径中间节点的次数来衡量该节点的重要性。一个结点充当“中介”的次数越多,它的中介中心度就越大。如果要考虑标准化的问题,可以用一个结点承担最短路桥梁的次数除以所有的路径数量。
2.4 PageRank
PageRank可以算作是目前Centrality类中最经典的算法,PageRank不但考虑了Degree算法中出度入度数量对于节点重要性的影响,同时考虑了邻居节点的重要程度对结果的影响。PageRank的多个变种已经在搜索引擎的网页排序中被广泛使用,经典的应用是基于web超链接的互相引用计算出每个web的重要程度,之后依照重要程度进行排序。PageRank递归定义一个节点的影响基于引用它节点的影响,即如果一个顶点有更多的引用顶点,或者它的引用顶点有更高的影响,那么这个顶点的影响就会增加,这种定义方式也类似于我们对传统社会中个人影响力的认知。
PageRank是基于随机网络冲浪者模型来计算各节点得分的,在该模型中,一个顶点的PageRank得分与一个随机网络浏览者在任何给定时间出现在该顶点的概率成正比,从而保证具有较高PageRank分数的节点是一个经常访问的顶点。该模型的假设如下:
1、 事物当前的状态只与其上一个状态有关
2、 一个节点(网页)的入度(被链接数)越大,得分越高
3、 一个节点(网页)的入度的来源(哪些网页在链接它)得分越高,得分越高
4、 处于各节点(网页)的用户会存在一定的概率
以上是关于基于图数据的数据挖掘及相关算法介绍的主要内容,如果未能解决你的问题,请参考以下文章