机器学习其它降维方法

Posted 2021-04-27 稷殿下

目录

• 目录

• 概率主成分分析

• 讨论

• PCA的优点

• PCA的局限性

• PCA vs. LDA

• 核主成分分析

• 等距映射（ISO-Metric Mapping）

• 概述

• 计算步骤

• 优缺点

• 局部线性嵌入

• Local Linear Embedding (LLE)

• 计算过程

• 简单例子

概率主成分分析

• PCA 的概率表示

隐变量 以如下形式产生 维观测变量

其中， 为均值， 为高斯噪声。 为 维的隐变量，且满足高斯分布

以 为条件的分布也满足高斯分布

以有向图表示

• 从隐空间到数据空间的映射，与 PCA 的传统视角相反
• 从数据空间到隐空间的映射，可以由 贝叶斯定理得到

1 维隐变量空间 - 2 维数据空间 - 边缘分布的等密度线

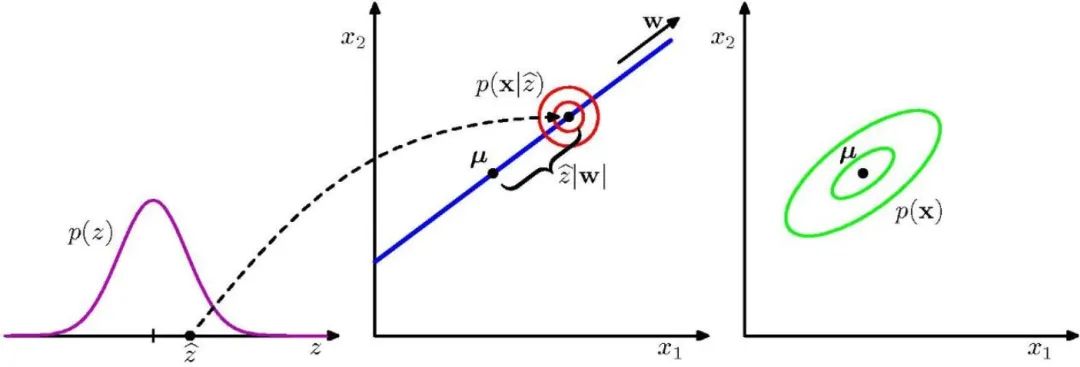
根据贝叶斯定理，有

其中

因此

一般利用最大似然估计进行求解，给定 ，求其对数似然函数

对 求导并置为 0 得

于是，有

代入似然函数，有

其中 为相关矩阵。因此

讨论

PCA的优点

• 具有很 高普适性，最大程度地保持了原有数据的信息；
• 可对 主元的重要性进行排序，并根据需要略去部分维数，达到降维从而简化模型或对数据进行压缩的效果；
• 完全 无参数限制，在计算过程中不需要人为设定参数或是根 据任何经验模型对计算进行干预，最终结果只与数据相关。

PCA的局限性

• 假设模型是 线性的，也就决定了它能进行的主元分析之间的关系也是线性的；
• 假设概率分布模型是 指数型；
• 假设数据具有 较高信噪比，具有最高方差的一维向量被看作是主元，而方差较小的变化被认为是噪声

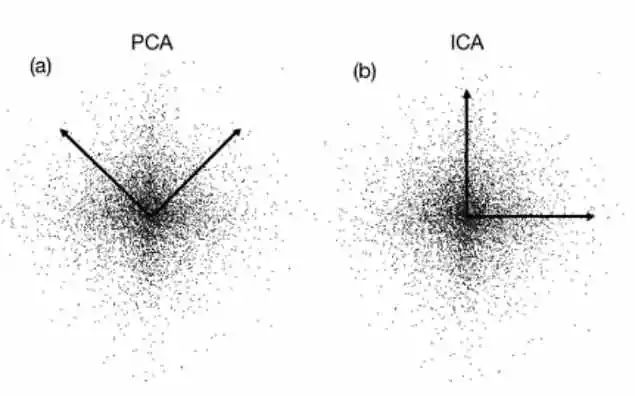
PCA vs. LDA

• PCA 追求降维后能够最大化保持数据内在信息，并通过衡量在投影方向上的数据方差来判断其重要性。但这 对数据的区分作用并不大，反而可能使得数据点混杂在一起。

PCA ( ) vs LDA ( )

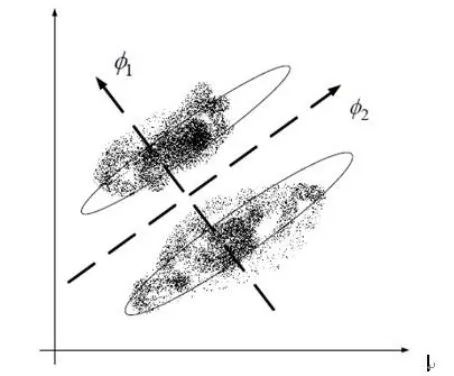
• LDA 所追求的目标与 PCA 不同，不是希望保持数据最多的信息，而是希望数据在降维后能够 很容易地被区分开。

PCA ( ) vs LDA ( )

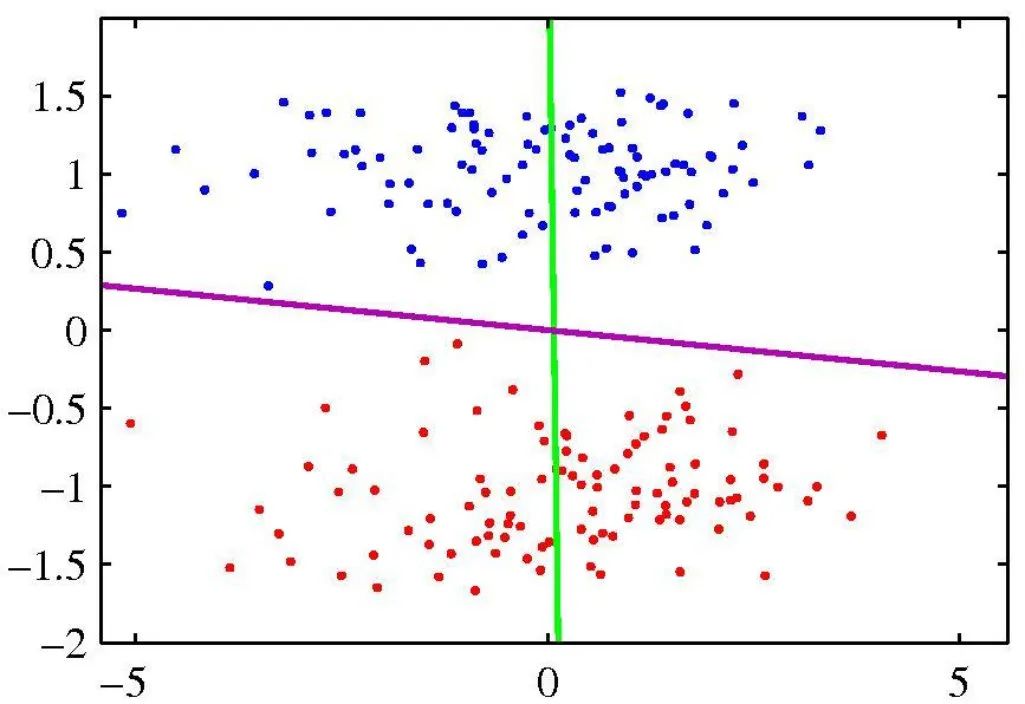
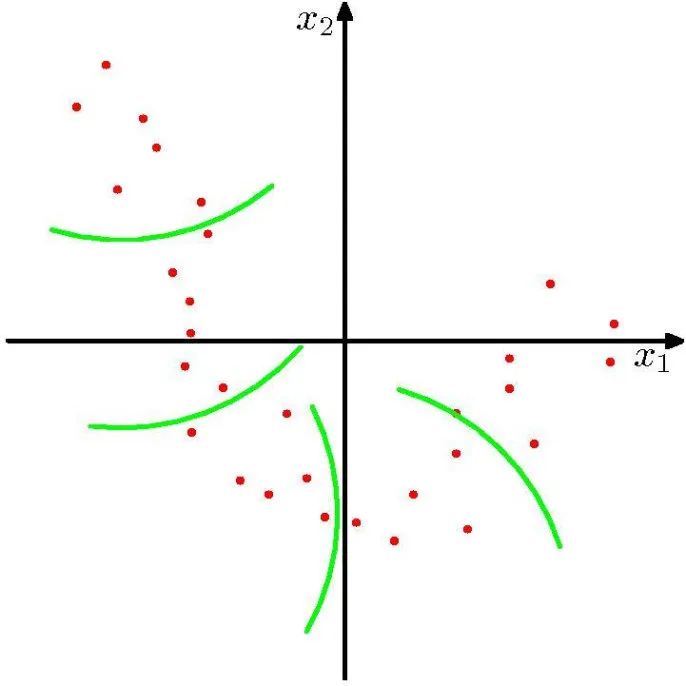
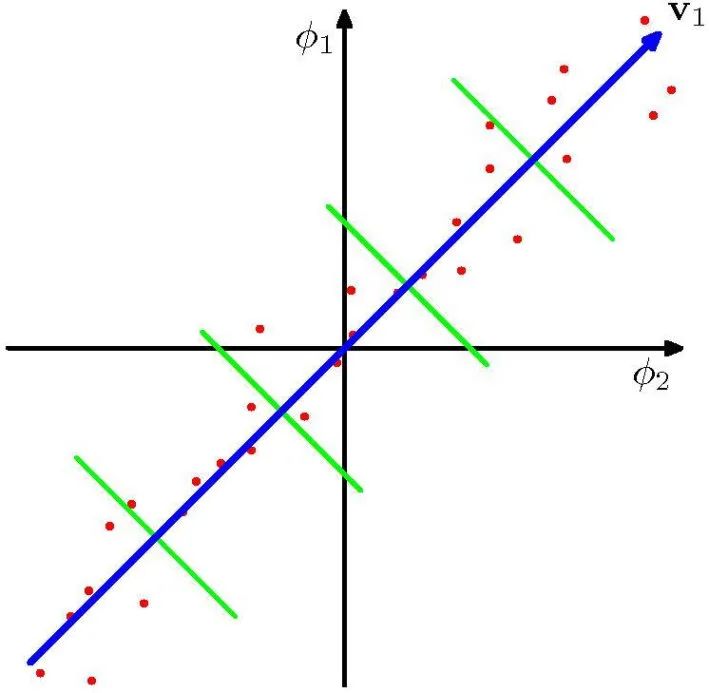
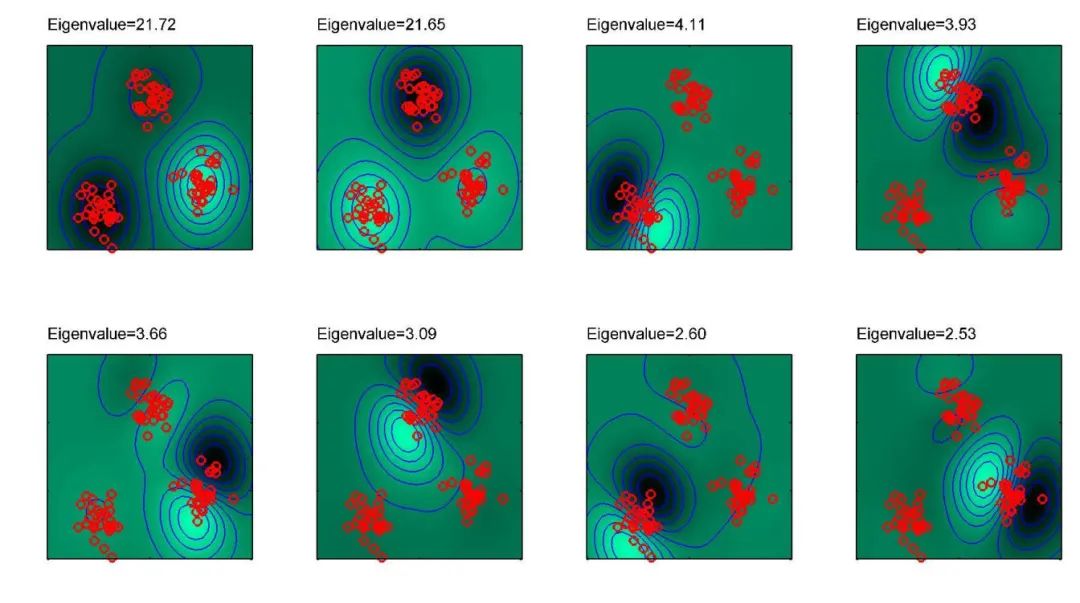
核主成分分析

将主成分分析的线性假设一般化使之适应非线性数据

• 传统 PCA： 维样本 ，

• 核 PCA：非线性映射 ，

核 PCA

核 PCA

核 PCA

等距映射（ISO-Metric Mapping）

概述

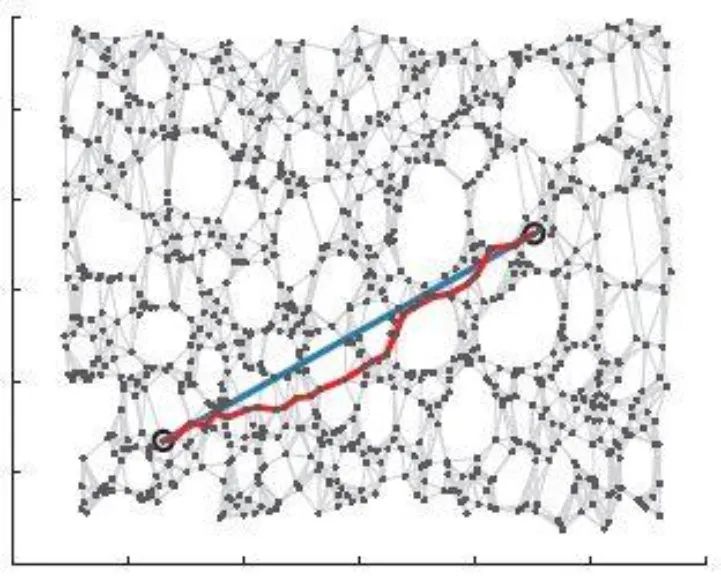
等距映射的思想：保持数据点内在几何性质 (测地距离)

测地距离与欧氏距离

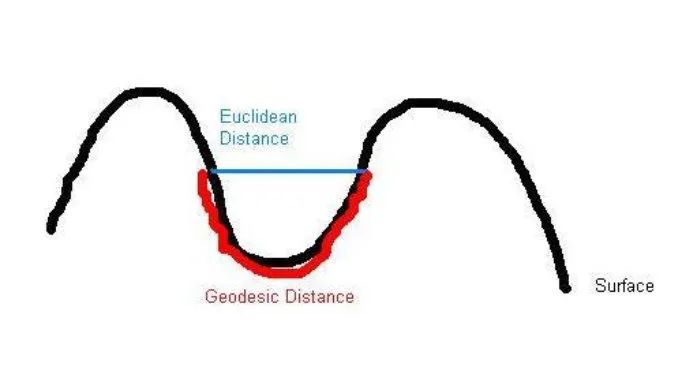
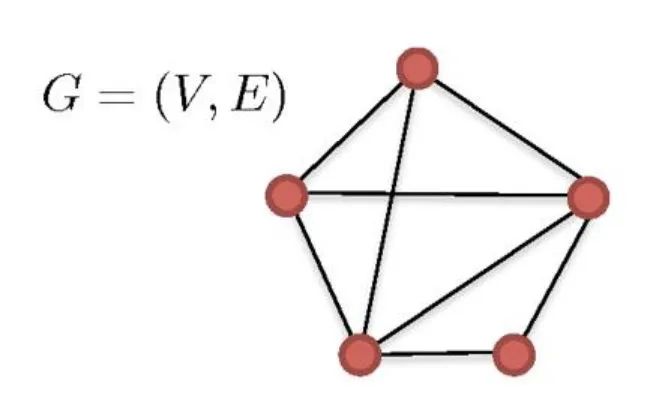
对给定数据 ，构造图 。其中 是顶点集合， 是边的集合。若 小于某个值 （ -ISOMAP），或 是 的 近邻（ -ISOMAP），则顶点 和 的边权值设为 ，否则为 0。

图

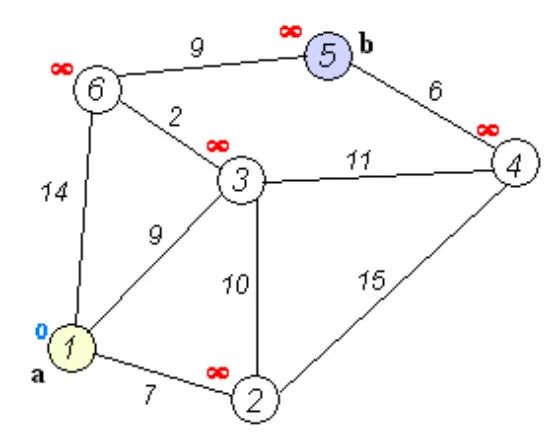
计算图 中任意两点间的最短距离，得到矩阵 ，可选算法有

• Dijkstra 最短路径算法
• Floyd–Warshall 算法

带权图

-近邻

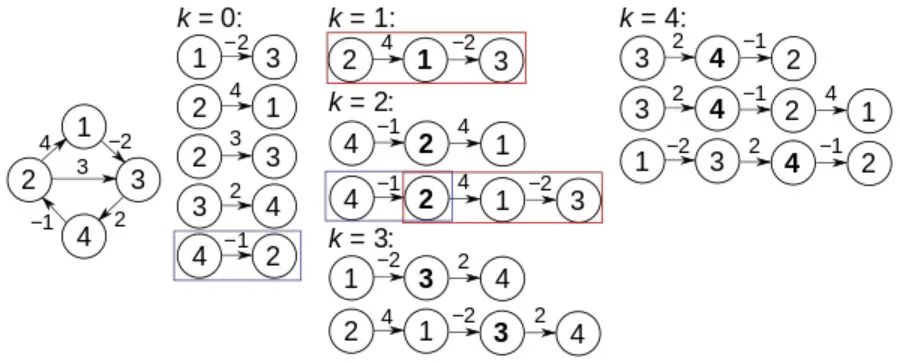
令 为中心矩阵（Centering Matrix），并定义平方距离矩阵

求矩阵 的特征值与特征向量（按特征值降序排列）， 为第 个特征值， 为对应的特征向量。则，降维矩阵为

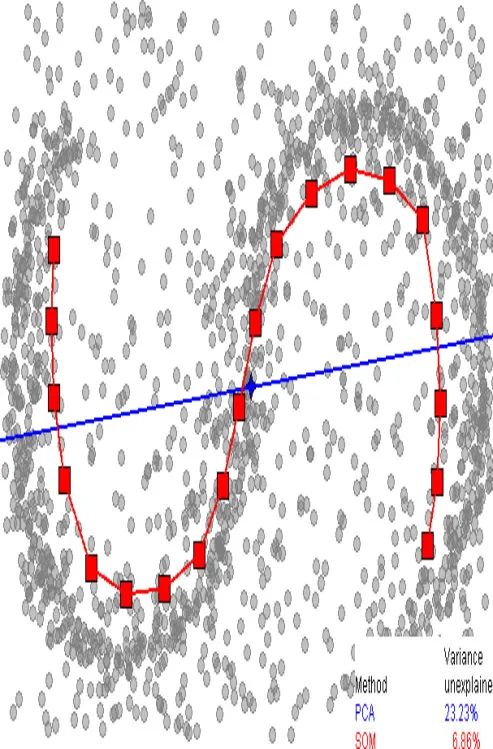
例如，原始数据如下：

原始数据

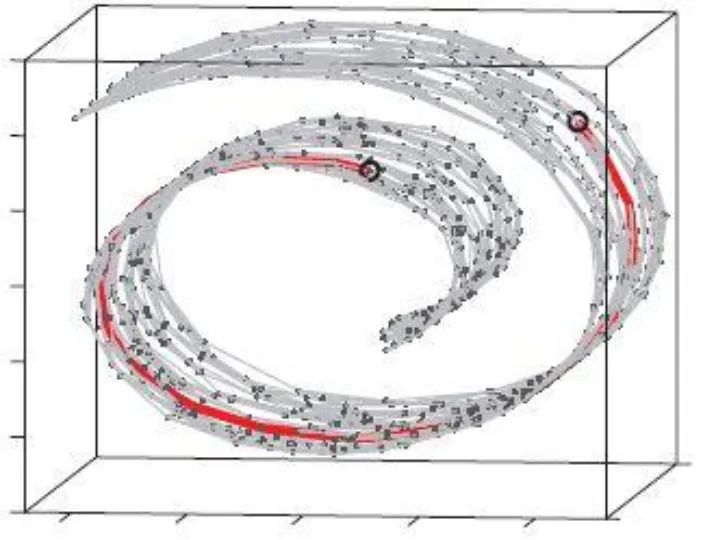
等距映射后的数据如下：

降维后数据

计算步骤

• 构造临近关系图：对每一个点，将它与指定半径邻域内所有点相连(或与指定个数最近邻相连)
• 计算最短路径：计算临近关系图所有点对之间的最短路径，得到距离矩阵
• 多尺度分析：将高维空间中的数据点投影到低维空间，使投影前后的距离矩阵相似度最大

优缺点

• 优点：非线性、非迭代、全局最优、参数可调节
• 缺点：容易受噪声干扰、在大曲率区域存在短路现象、不适用于非凸参数空间、大样本训练速度慢

局部线性嵌入

Local Linear Embedding (LLE)

基本思想：保持数据点的原有流形结构

Local Linear Embedding (LLE)

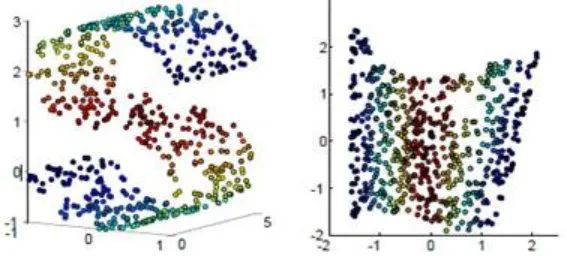
前提假设：采样数据所在的低维流形在局部是线性的，每个采样点可以用它的近邻点线性表示。学习目标：在低维空间中保持每个邻域中的权值不变，即假设嵌入映射在局部是线性的条件下，最小化重构误差。

计算过程

• 寻找每个样本点的 近邻
• 对每个点用 个近邻进行重建，即求一组权值 ，满足 ，使得

• 求低维空间中的点集 ，使得

• 计算权值，首先构造局部协方差矩阵

• 最小化

• 求得

• 计算低维数据

取 为 的最小 个非零特征值所对应的特征向量，最终的输出结果即为 大小的矩阵。

Local Linear Embedding (LLE) 计算步骤

简单例子

一个例子