机器学习最小二乘法

Posted 2021-04-27 李呆呆的学习笔记

一、简介

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。

二、生活中的例子

现在我有5把尺子，分别用它们来测量一段线段的长度，得到的测量值分别为（不同颜色代表不同尺子）：

尺子	长度
红	10.2
蓝	10.3
橙	9.8
黄	9.9
绿	9.8

为什么测量值会不一样：

• 不同厂家生产的尺子的精度不同

• 尺子的材质不同，热胀冷缩的程度不一样

• 测量的人造成的测量误差

• ……

总之，就是有误差存在，误差是不可避免的。

 

得到了5把尺子测量的值，那个这段线段的长度到底要标多长呢？

通常我们的做法是计算五次测量值的算术平均数，作为这段线段的长度。即：

思考：虽然大家都是这么做，但是这么做有没有问题？

 

转换最小二乘法的思路思考上述问题：

• 首先，将五把尺子的测量值画到坐标系中，分别标为y_i：

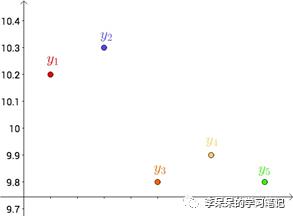
• 其次，猜测这段线段的真实长度为y，并在坐标轴中用虚线标出来：

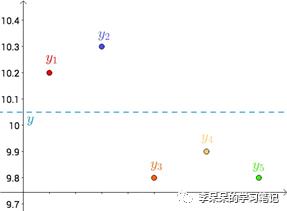
• 每个点都向y做垂线，垂线的长度就是|y-y_i|，也可以理解成是测量值和真实值之间的误差（误差是随机的，概率分布符合正态分布）：

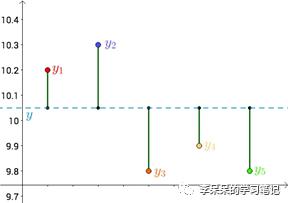
由于|y-y_i|要计算绝对值，比较麻烦，所以最小二乘中直接将y-y_i取平方来代表误差：

|y-y_i|à(y-y_i)²

• 最小二乘法就是想要寻找一个使误差平方和最小的y值，这个y值就近似成真实的y值。

误差平方和:=(y-y_i)²

因为y是猜测的，所以这个y是不断变化的：

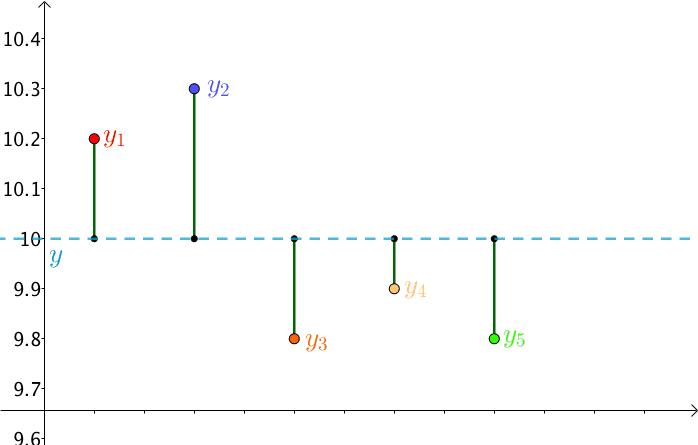
由于y在不断变化，那么也在不断变化。

最小二乘法的思想就是，当误差平方和达到最小时，那个y值就近似为真实的y值。

 

所以，我们就是要求的最小值，即求极值的问题（函数在极值点时，导数为0）

接下来进行计算：

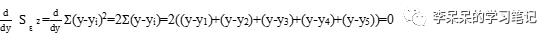
即：

正好是算术平均数。

三、一元线性模型

例子：

数据：温度和冰淇淋的销量

温度	销量
25	110
27	115
31	155
33	160
35	180

目的：得出一个能使上述数据大体适合的经验公式。

• 首先将温度和冰淇淋销量对应数值在坐标系上表示出来：

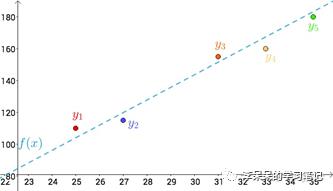
• 从上图可以看出两者的关系类似线性关系，因此假设这种线性关系为：

f(x)=ax+b

根据最小二乘法的思想，误差平方和：

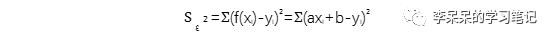
a和b是未知数，当a和b取不同的值时，误差平方和不同。最适合的经验公式是当误差平方和最小时ab对应的函数。

因此计算如下：

分别对a、b求导：

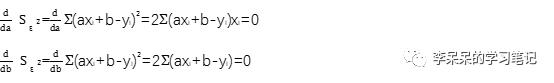
联立上述两式得到a=7.2 b=-73，即f(x)=7.2x-73是最能体现温度和冰淇淋销量的关系。

四、多元线性模型

数据：

温度	湿度	…	销量
25	10.3	…	110
27	20.3	…	115
31	15.6	…	155
33	21.9	…	160
35	10.8	…	180

 

上述的一元模型中只有一个变量x（温度），假如影响冰淇淋销量的因素还有很多比如：x1(温度),x2（天气）,x3（湿度）……xn,那么线性函数就可以用如下函数表示：

y=β₀+β₁x₁+β₂x₂+β₃x₃+β₄x₄……+β_nx_n

对于观测到的m个销售量（样本量m≥变量数n）来说，就可以用如下线性方程组表示：

y₁=β₀+β₁x₁₁+β₂x₁₂+β₃x₁₃+β₄x₁₄……+β_nx_1n

y₂=β₀+β₁x₂₁+β₂x₂₂+β₃x₂₃+β₄x₂₄……+β_nx_2n

……

y_m=β₀+β₁x_m1+β₂x_m2+β₃x_m3+β₄x_m4……+β_nx_mn

如果将样本矩阵xij记为矩阵A，将参数矩阵记为向量β，真实值记为向量Y，上述的线性方程组就可以表示为：

即：Aβ=Y

根据最小二乘的思想，要使误差平方和最小，最终的矩阵表达式为：

经过求导最终得到β=(A^TA)^-1A^TY,它是一个全局最优解。