生成式模型入门： GAN 与 VAE——“以假乱真”的哲学

Posted 2023-03-15

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了生成式模型入门： GAN 与 VAE——“以假乱真”的哲学相关的知识，希望对你有一定的参考价值。

参考技术A

在图像处理中，比较常见的任务有识别、检测、追踪等，这些任务的模型通常在训练阶段通过参数估计学得如何提取输入图像的特征，并建立输入图像与输出之间的映射，在应用阶段之间提取输入图像的特征，以得到相应的结果。

但有这样一类特殊的模型，其参数估计的目的不是通过提取特征来建立输入输出之间的映射，而是学习训练数据的分布，从而模型在应用阶段能够生成与训练数据相似的图像，通常这些图像与真实图像极为相似，我愿称之为“以假乱真”的哲学，这类模型就是 生成式模型 。

基于特定分布进行数据生成，是近年来机器学习领域研究和落地，通常由由模型通过学习一组数据的分布，然后生成类似的数据。在机器学习领域，主流的生成模型共有 4 类：

这 4 类模型是基于不同的原理构建的，在本文中，我将介绍最常被用到的两类模型—— GAN 和 VAE。

生成式对抗网络（Generative adversarial net, GAN）是一种基于对抗学习的深度生成模型，最早由 Ian Goodfellow 在《Generative Adversarial Nets》提出，一经提出就成为了学术界研究的热点，Ian Goodfellow 也因此被人称为“GANs 之父”（没错，就是那个写了花书的大佬ヾ(≧▽≦*)o ）。

想必看过金庸小说的同学们都知道，“老顽童”周伯通有一样异于常人的本领——左右互博，有了这样一门武功，一来只有自己一个人也能玩得不亦乐乎，二来自己一个人就能切磋武艺。那是不是神经网络也可以通过这种方式来“修炼功夫”？对抗学习就是基于这样的思想。

GAN 的思想很简单，总结起来就是 以假乱真、相互对抗 ，而它的做法也是非常之简单粗暴，同时（或者说交替）训练两个网络，通过两个网络之间的博弈，从而达到互相促进的作用。

在 GAN 的整体框架中，用于训练的模型由两个网络组成，一个网络是 生成器 G （generator），用于数据的生成；另一个网络是 判别器 D （discriminator），用于对生成器生成的数据和训练数据进行真假判别。就拿图像生成为例，在图像生成模型的训练过程中：

在训练过程中，生成器和判别器就像是两个相互博弈的人，生成网络 G 的目标就是尽量生成真实的图像去欺骗判别网络 D ，而 D 的目标就是尽量把 G 生成的图片和真实的图片分别开来。通过相互对抗，生成网络的生成能力和判别网络的判别能力将越来越强，最终当模型收敛时，我们将得到一个生成效果较好的生成器。

为了描述 GAN 如何完成这个博弈过程，我们先定义 GAN 目标函数：

让我来解释一下这个公式：

借用论文里的一张图来说明这个过程，如下图：

在实际实现中，两个网络的更新是交替进行的，这导致在超参数调节不合适时，会出现参数更新不平衡的问题，不过这个问题不是这篇博客讨论的重点，暂且挂起不谈。

其训练过程如下图所示（来自原论文）：

可以看到，在每一轮迭代中：

GAN 依然存在一些缺点，比如说训练不稳定，生成过程不可控，不具备可解释性等，于是后来出现了若干改进的版本。

当卷积神经网络再视觉领域大放光彩后，有人尝试将卷积操作融合到 GAN 中，也就是接下来要讲的深度卷积对抗生成网络（DCGAN）。

DCGAN 在《UNSUPERVISED REPRESENTATION LEARNING WITH DEEP CONVOLUTIONAL GENERATIVE ADVERSARIAL NETWORKS》被首次提出，是基于 GAN 的基本框架构建的生成模型，相比于 GAN ，它有了如下的改进：

DCGAN 的网络结构如下图：

DCGAN的训练过程与 GAN 相同，不过由于网络结构的改变，相比于 GAN ，DCGAN 的训练相对平衡，并且对局部特征的提取和还原能力较 GAN 强。但由于 DCGAN 属于早期的 GANs ，所以依然存在部分 GAN 的问题，在 DCGAN 后 GAN 又有了若干改进版，由于数量较多、有的比较水，这里就暂且挂起，不多叙述。

如果说 GAN 在数据生成模型领域为我们选择了一条简单粗暴的道路，那接下来要讲的模型则为我们提供了更加巧妙的办法。

变分自编码器（variational autoencoder, VAE）采用变分推断的方式来构建，与其他自编码器类似，变分自编码器也是由编码器和解码器组成，其本质是对一个含隐变量的函数进行密度估计。在训练过程中， VAE 的主要目的是进行极大似然估计，为了使得隐变量服从某一分布，在参数估计的过程中采用了变分推断的思想。

假设我们现在需要在某系统中，估计模型的后验概率，而这个的计算非常复杂，其中是隐变量，是显变量。

针对这一问题，在变分推断中，我们希望望找到一个相对简单好算的概率分布，使它尽可能地近似我们待分析地后验概率，以求我们能够用来近似。所以，为了度量两个概率分布和之间的距离，我们需要用到的一个工具就是 KL 散度 。

KL 散度（Kullback-Leibler divergence）即相对熵，两个概率分布间差异的非对称性度量。如果两个分布越接近，那么 KL 散度越小，如果越远，KL 散度就会越大。对于两个分布和，其 KL 散度的公式为：

假设我们有一个判别任务，现有一个等待判别的事物，这个事物有一个类别，我们需要建立一个模型使得的概率尽可能大，即让尽可能地接近。

如果我们使用生成式模型去解决这一问题，就需要用贝叶斯公式将这个问题转换成：

让我们再考虑一下数据生成问题，则问题可以转换成：当我们有式子左边的，应该如何生成一个符合某种的（其中为符合某种分布的隐变量）？

一个解决方式是：每次随机生成一个，用计算概率，如果概率满足，则结束，如果不满足，则继续随机生成。但这种方式在某些情况下是不现实的，特别是右部的公式难以直接计算得到，所以，我们需要采用其他可行的方法来解决这一问题。这时就可以用到变分推断的思想结合自编码器，假设隐变量服从某种分布来解决这一问题。

由于公式（2）中，右部的积分公式难以计算，我们可以用一个变分函数去代替。在 VAE 中，这个函数将采用编码器实现），当编码器能够将数据能够完美地将真实数据编码成服从一定分布的隐变量时，那解码器就能将服从这一分布的隐变量解码成接近真实数据的生成数据，从而解码器将能作为生成器使用，这便是 VAE 的基本思想 。

为了能采用去代替，我们需要使得两个分布布尽可能地相近，于是乎我们选择了 KL 散度这个指标用来衡量两者的相近程度，于是有：

左右整理一下，我们可以得到：

我们知道在给定的情况下，是个固定值，而我们的目的是最大化，所以我们需要让等号右边那部分尽量大，所以，为了找到一个好的，使得它和尽可能地相近，我们需要：

为了将数据编码到隐变量，我们需要假设隐变量服从某种分布。通常我们假设服从高斯分布，则计算公式为：

为了计算方便，我们再进行一个比较强的假设，假设隐变量服从标准正态分布，即服从均值为，方差为单位矩阵的高斯分布，则：

接下来，我们就能通过构建编码器，得到一个由输入求解隐变量的函数，利用梯度下降法，可根据公式（6）对网络参数进行优化，使得编码器近似接近我们想要拟合的函数。

而对于公式（4）的第一项，我们可以通过构建一个从再变回的解码器，通过梯度下降法进行解码器参数优化，从而实现对的极大似然估计，我们将得到一个将符合高斯分布的隐变量变成生成数据的生成器。

条件变分自编码器（CVAE）是 VAE 的变种。VAE 是无监督学习，但是当我们需要网络能够根据我们的需要生成特定的图片，需要加入标签 y 辅组训练，这就是 CVAE。

CVAE 可以看作是有监督学习的 VAE 。将公式（4）的右部变为：

在这里，自编码器需要重构的是而不是 , 所以最终的生成器能够根据标签进行采样而生成对应的数据。

在TensorFlow中对比两大生成模型：VAE与GAN

选自GitHub

机器之心编译

参与：路雪、李泽南

变分自编码器（VAE）与生成对抗网络（GAN）是复杂分布上无监督学习最具前景的两类方法。本文中，作者在 MNIST 上对这两类生成模型的性能进行了对比测试。

项目链接：https://github.com/kvmanohar22/Generative-Models

本项目总结了使用变分自编码器（Variational Autoencode，VAE）和生成对抗网络（GAN）对给定数据分布进行建模，并且对比了这些模型的性能。你可能会问：我们已经有了数百万张图像，为什么还要从给定数据分布中生成图像呢？正如 Ian Goodfellow 在 NIPS 2016 教程中指出的那样，实际上有很多应用。我觉得比较有趣的一种是使用 GAN 模拟可能的未来，就像强化学习中使用策略梯度的智能体那样。

本文组织架构：

变分自编码器（VAE）
生成对抗网络（GAN）
训练普通 GAN 的难点
训练细节
在 MNIST 上进行 VAE 和 GAN 对比实验

在无标签的情况下训练 GAN 判别器
在有标签的情况下训练 GAN 判别器

在 CIFAR 上进行 VAE 和 GAN 实验
延伸阅读

VAE

变分自编码器可用于对先验数据分布进行建模。从名字上就可以看出，它包括两部分：编码器和解码器。编码器将数据分布的高级特征映射到数据的低级表征，低级表征叫作本征向量（latent vector）。解码器吸收数据的低级表征，然后输出同样数据的高级表征。

从数学上来讲，让 X 作为编码器的输入，z 作为本征向量，X′作为解码器的输出。

图 1 是 VAE 的可视化图。

图 1：VAE 的架构

这与标准自编码器有何不同？关键区别在于我们对本征向量的约束。如果是标准自编码器，那么我们主要关注重建损失（reconstruction loss），即：

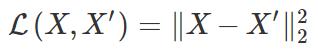
在TensorFlow中对比两大生成模型：VAE与GAN

而在变分自编码器的情况中，我们希望本征向量遵循特定的分布，通常是单位高斯分布（unit Gaussian distribution），使下列损失得到优化：

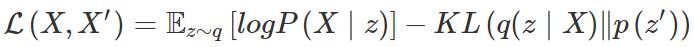
在TensorFlow中对比两大生成模型：VAE与GAN

p(z′)∼N(0,I) 中 I 指单位矩阵（identity matrx），q(z∣X) 是本征向量的分布，其中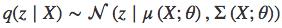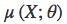在TensorFlow中对比两大生成模型：VAE与GAN 。和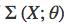由神经网络来计算。KL(A,B) 是分布 B 到 A 的 KL 散度。

由于损失函数中还有其他项，因此存在模型生成图像的精度和本征向量的分布与单位高斯分布的接近程度之间存在权衡（trade-off）。这两部分由两个超参数λ_1 和λ_2 来控制。

GAN

GAN 是根据给定的先验分布生成数据的另一种方式，包括同时进行的两部分：判别器和生成器。

判别器用于对「真」图像和「伪」图像进行分类，生成器从随机噪声中生成图像（随机噪声通常叫作本征向量或代码，该噪声通常从均匀分布（uniform distribution）或高斯分布中获取）。生成器的任务是生成可以以假乱真的图像，令判别器也无法区分出来。也就是说，生成器和判别器是互相对抗的。判别器非常努力地尝试区分真伪图像，同时生成器尽力生成更加逼真的图像，使判别器将这些图像也分类为「真」图像。

图 2 是 GAN 的典型结构。

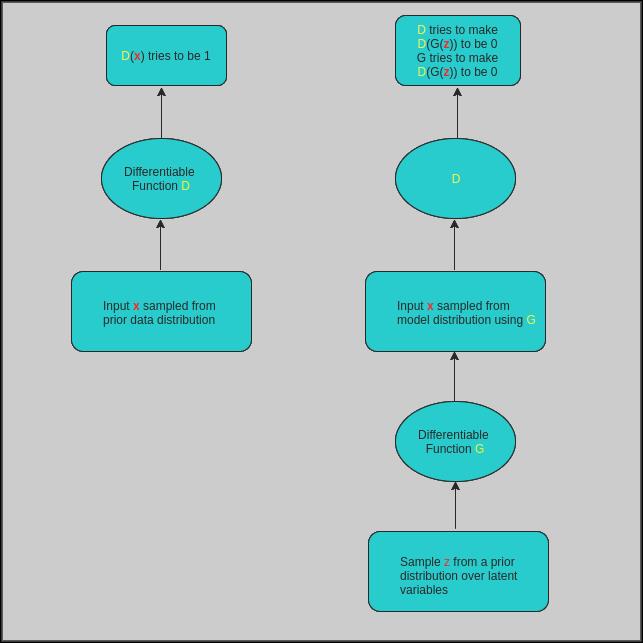
在TensorFlow中对比两大生成模型：VAE与GAN

图 2：GAN

生成器包括利用代码输出图像的解卷积层。图 3 是生成器的架构图。

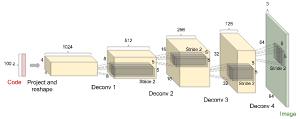
在TensorFlow中对比两大生成模型：VAE与GAN

图 3：典型 GAN 的生成器图示（图像来源：OpenAI）

训练 GAN 的难点

训练 GAN 时我们会遇到一些挑战，我认为其中最大的挑战在于本征向量／代码的采样。代码只是从先验分布中对本征变量的噪声采样。有很多种方法可以克服该挑战，包括：使用 VAE 对本征变量进行编码，学习数据的先验分布。这听起来要好一些，因为编码器能够学习数据分布，现在我们可以从分布中进行采样，而不是生成随机噪声。

训练细节

我们知道两个分布 p（真实分布）和 q（估计分布）之间的交叉熵通过以下公式计算：

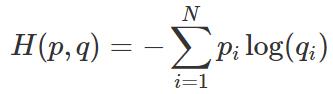
在TensorFlow中对比两大生成模型：VAE与GAN

对于二元分类，

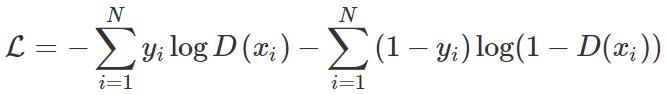
在TensorFlow中对比两大生成模型：VAE与GAN

对于 GAN，我们假设分布的一半来自真实数据分布，一半来自估计分布，因此：

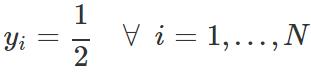
在TensorFlow中对比两大生成模型：VAE与GAN

训练 GAN 需要同时优化两个损失函数。

按照极小极大值算法，

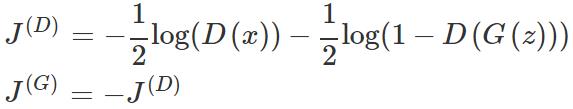
在TensorFlow中对比两大生成模型：VAE与GAN

这里，判别器需要区分图像的真伪，不管图像是否包含真实物体，都没有注意力。当我们在 CIFAR 上检查 GAN 生成的图像时会明显看到这一点。

我们可以重新定义判别器损失目标，使之包含标签。这被证明可以提高主观样本的质量。

如：在 MNIST 或 CIFAR-10（两个数据集都有 10 个类别）。

上述 Python 损失函数在 TensorFlow 中的实现：

    def VAE_loss(true_images, logits, mean, std):      """        Args:          true_images : batch of input images          logits      : linear output of the decoder network (the constructed images)          mean        : mean of the latent code          std         : standard deviation of the latent code      """      imgs_flat    = tf.reshape(true_images, [-1, img_h*img_w*img_d])      encoder_loss = 0.5 * tf.reduce_sum(tf.square(mean)+tf.square(std)                     -tf.log(tf.square(std))-1, 1)      decoder_loss = tf.reduce_sum(tf.nn.sigmoid_cross_entropy_with_logits(                     logits=logits, labels=img_flat), 1)      return tf.reduce_mean(encoder_loss + decoder_loss)

    def GAN_loss_without_labels(true_logit, fake_logit):      """        Args:          true_logit : Given data from true distribution,                      `true_logit` is the output of Discriminator (a column vector)          fake_logit : Given data generated from Generator,                      `fake_logit` is the output of Discriminator (a column vector)      """      true_prob = tf.nn.sigmoid(true_logit)      fake_prob = tf.nn.sigmoid(fake_logit)      d_loss = tf.reduce_mean(-tf.log(true_prob)-tf.log(1-fake_prob))      g_loss = tf.reduce_mean(-tf.log(fake_prob))      return d_loss, g_loss

    def GAN_loss_with_labels(true_logit, fake_logit):      """        Args:          true_logit : Given data from true distribution,                      `true_logit` is the output of Discriminator (a matrix now)          fake_logit : Given data generated from Generator,                      `fake_logit` is the output of Discriminator (a matrix now)      """      d_true_loss = tf.nn.softmax_cross_entropy_with_logits(                    labels=self.labels, logits=self.true_logit, dim=1)      d_fake_loss = tf.nn.softmax_cross_entropy_with_logits(                    labels=1-self.labels, logits=self.fake_logit, dim=1)      g_loss = tf.nn.softmax_cross_entropy_with_logits(                    labels=self.labels, logits=self.fake_logit, dim=1)      d_loss = d_true_loss + d_fake_loss      return tf.reduce_mean(d_loss), tf.reduce_mean(g_loss)