数字金融与算法研究（十九）—基于BP神经网络的股价预测

Posted 2021-04-26 数字金融研修社

基于BP神经网络的股价预测

在金融系统的预测研究中，股价预测是一个相当热门的课题，由于股票市场具有高风险与高收益的特性，使得股价预测有非常大的应用价值。传统的统计方法可以预测一段时间内股指的大致走势，然而短期内的股指涨跌往往更加吸引大多数投资者的关注。近十几年来计算机技术以及人工智能技术的快速发展为股价预测提供了许多新的方法，BP神经网络正是其中之一，其在经济金融领域受到了广泛的应用。

1

BP神经网络

BP神经网络采用的是BP算法，全称为误差反向传播算法，顾名思义，其基本特征就是误差的逆向传播。BP神经网络模型主要分为三个部分：输入层、隐含层以及输出层（如图1），相邻两层各神经元之间相互连接，连接强度由权重决定，同层神经元之间没有反馈，其学习过程有两个，即信息正向传播以及误差的反向传播。信息的正向传播过程是指将输入样本从输入层传入隐含层，再传到输出层的过程。隐含层和输出层的各神经元上会有激活函数对传入的数据进行处理，产生相应的输出。若输出层的实际输出与期望的输出有较大误差，那将会进行第二个过程，误差的反向传播，该过程将输出误差通过隐层的作用回传给输入层，并且将误差均分给各层的所有神经元，从而获得各层神经元的误差信号，此误差信号即作为修正各神经元权值的依据，通过这种循环往复的修正传播，模型可以自动调整权值直至误差达到预期值。

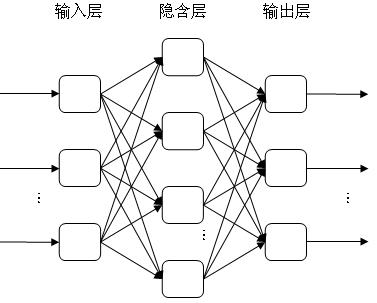
图1.BP神经网络

对于具体的研究问题来说，输入单元数以及输出单元数已经是确定的，需要确定的就是隐含层的的层数以及单元数，隐含层的层数可以通过实际研究对象的情况来确定，但是隐含层单元数的判定却是个较为复杂的问题。单元数量过少会导致模型训练和预测的精度降低，进而导致模型实证效果不佳；而单元数量过多则会减弱模型的概括推理能力，因此，BP神经网络模型的有效性取决于隐含层的层数以及其单元数。研究者往往采用试凑法来确定最优的隐含层单元数，即初始时设置较少的单元数，计算其误差，随后逐渐增加单元数，对所有误差值进行比较，挑选出误差最小的隐含层单元数。在使用试凑法时，可以通过以下公式来初步估计隐含层节点数：

其中，m为输入层神经元数，n为输出层神经元数，a为0-10之间的常数。

在确定隐含层的层数以及单元数之前，需要选择激活函数，BP神经网络的激活函数为非线性并且可微的非递减函数，一般选取（0，1）之间的S型函数，其能够强化网络的非线性映射能力，比如f（x）=1/（1+exp（-x））。但是对于输出层来说，只有在希望对输出进行限制的情况下，才会在输出层采用S型函数，否则输出会被限制在一个很小的范围内，在一般情况下，均是在隐含层采用S型函数，而输出层采用线性函数，这样可以使神经网络输出任何值。

BP神经网络学习规则的知道思想为：寻找表现函数下降最快的方向，然后按此方向对神经网络的权值和阂值进行修正。

其中，xk是模型中k时刻的权值和阈值矩阵，η是学习率，也称为步长，gk是当前表现函数的梯度。以三层BP神经网络模型为例，即只有一个隐含层，假设输入层节点为xi，隐含层节点为yj，输出层节点为zl。输入节点与隐含层节点间的权值为wji，隐含层节点与输出节点之间的权值为vlj。零输出层节点的期望值为tl，那么有：

隐含层节点的输出为：

输出层节点的输出为:

输出层的节点误差为：

输出层误差函数分别通过对输出层节点的输出以及隐含层节点的输出求导，经过计算可得出结论：权值得修正量△vlj，△wji要与误差函数保持正比，并沿梯度下降，并且有：

根据以上的分析，可以将BP算法分为5个步骤：

①. 初始化网络以及各个参数，包括输入层、输出层得节点数，隐含层层数和节点数以及赋予各节点的连接权值，神经元阈值（-1，1）之间的随机数；

②. 选择训练模式，并将预测集信息传入输入层；

③. 正向传播过程，从第一隐含层开始，对传入的输入信息进行计算，将输出结果与期望值相比较，若有误差，则执行第4步；否则，返回第2步，进入下一个训练模式；

④. 反向传播过程，从输出层反向计算到输入层，并通过以上方式修正各单元的连接权值，修正阈值的方式与权值类似；

⑤。返回第2步，循环训练，直到每一个训练模式均满足期望。

2

BP神经网络的局限性

①. BP神经网络最大的一个缺陷就是由于非线性函数可能存在多个局部最优解，使得在寻找最优解的过程中，容易陷入局部最小值的困境，这与初始值的选取有很大关系，如果初始值更接近局部最优解，而非全局最优解，那么就无法得到正确的结果。许多学者正是围绕着这一点进行研究，寻找解决局部最优解的方案。

②. 由于训练中稳定性要求学习率很小，因此梯度下降法会使得训练的很慢，而提高学习率可能会导致网络的不稳定性，进而使结果不收敛，这样的模型是无效的。

③. BP神经网络的结构以及参数的确定也比较困难，神经元数目太少会造成网络的不适性,而神经元数目太多又会引起网络的过适性。

3

基于BP神经网络模型的改进

针对以上的局限性，众多学者对模型的修正及改进取得了不错的成效：曹晓、孙红兵（2017）针对现有算法存在预测精度低和滞后性大的缺点，提出了一种以BP神经网络和灰色GARCH模型建立的股票价格预测模型。在建立灰色GARCH模型的基础上，通过运用BP神经网络对灰色GARCH残差序列进行预测，之后利用误差预测值校正灰色GARCH模型的预测结果，实现高精度股票价格预测。刘佳祺等（2018）将BP模型与主成分分析法和遗传算法相结合，建立预测股票价格变化的动态PCA-GA-BP模型。实证结果表明，该模型能改善BP模型运算速度缓慢和易陷入局部最小值的缺点。还有部分学者将机器学习算法与BP算法相比较，发现了更适用于股价预测的新算法，比如熊炳忠（2018）基于稀疏贝叶斯极限学习机（SBELM）方法对股票价格进行建模预测。利用上证综合指数的市场数据对该模型与传统的BP神经网络学习算法的建模预测进行比较，发现前者的预测精度更高、泛化能力更强，具有较好的应用价值。

免责信息：本资讯中的信息均来源于公开可获得资料，作者力求准确可靠，但对这些信息的准确性及完整性不做任何保证，据此投资，责任自负。

主笔︱陈伟

指导︱翠山︱安歌︱周一