人人都能懂的机器学习——训练深度神经网络——学习率规划
Posted 苏小菁在编程
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了人人都能懂的机器学习——训练深度神经网络——学习率规划相关的知识,希望对你有一定的参考价值。
学习率规划
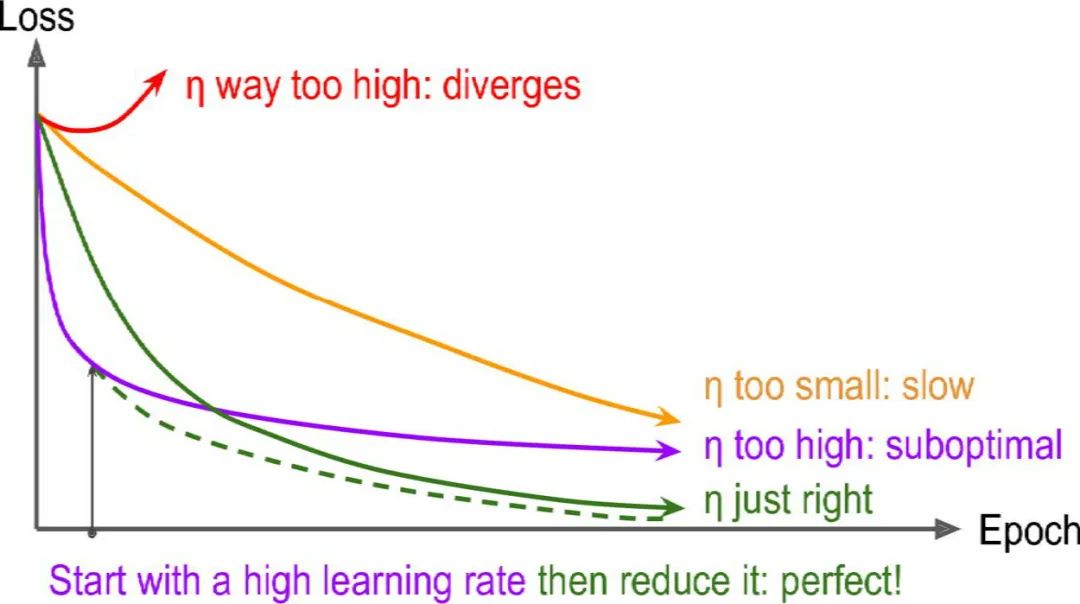
-
幂规划
-
指数规划
-
分段常数规划
-
性能规划
-
单循环规划
decay
超参数:
optimizer = keras.optimizers.SGD(lr=
0.01, decay=
1e-4)
decay
超参数是参数
s
的倒数,并且Keras假设
c
等于1。
def exponential_decay_fn(epoch):
return
0.01 *
0.1**(epoch /
20)
def exponential_decay(lr0, s):
def exponential_decay_fn(epoch):
return lr0 *
0.1**(epoch / s)
return exponential_decay_fn
exponential_decay_fn = exponential_decay(lr0=
0.01, s=
20)
LearningRateScheduler
回调函数,输入一个规划函数,然后将这个回调函数输入给
fit()
方法:
lr_scheduler = keras.callbacks.LearningRateScheduler(exponential_decay_fn)
history = model.fit(X_train_scaled, y_train, [...], callbacks=[lr_scheduler])
LearningRateScheduler
会在每个epoch开始的时候将优化器的learning_rate属性更新一次。一般来说每个epoch更新一次学习率就足够了,但是如果想要更加频繁地更新学习率,比如在每一步都更改学习率,那么可以写自己的回调函数。实际上如果每个epoch当中有很多步的话,对于每一步都更新学习率是有意义的。或者,可以使用
keras.optimizers.schedules
方法,在稍后会介绍这种方法。
def exponential_decay_fn(epoch, lr):
return lr *
0.1**(
1 /
20)
fit()
都会将epoch重新设为0。那么如果要在模型停止处继续训练,那么学习率可能会过大,那么可能会影响到模型权重。其中一种解决办法就是手动设置
fit()
方法中的
initial_epoch
参数,使得epoch从你想要的数字开始。
LearningRateScheduler
回调函数,并将其输入
fit()
方法,跟前面的方法一样:
def piecewise_constant_fn(epoch):
if epoch <
5:
return
0.01
elif epoch <
15:
return
0.005
else:
return
0.001
ReduceLROnPlateau
回调函数即可。比如,将下述回调函数传递给
fit()
方法,它会在连续5个验证损失不下降的epoch后,将学习率乘以0.5。
lr_scheduler = keras.callbacks.ReduceLROnPlateau(factor=
0.5, patience=
5)
keras.optimizers.schedules
中可用的规划来定义学习率,然后将学习率输入任意的优化器。这个方法会在每一步都更新学习率而不是每一个epoch。这里展示一下如何实现与上文相同的指数规划:
s =
20 * len(X_train) //
32
# number of steps in 20 epochs (batch size = 32)
learning_rate = keras.optimizers.schedules.ExponentialDecay(
0.01, s,
0.1)
optimizer = keras.optimizers.SGD(learning_rate)
self.model.optimizer.lr
来更新优化器的学习率)。
以上是关于人人都能懂的机器学习——训练深度神经网络——学习率规划的主要内容,如果未能解决你的问题,请参考以下文章