图神经网络及其在知识图谱中的应用

Posted 2021-04-26 中国计算机学会

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了图神经网络及其在知识图谱中的应用相关的知识，希望对你有一定的参考价值。

本文回顾了图神经网络模型的发展现状，对图神经网络的表达及推理能力进行探讨。最后，基于知识图谱的表示形式，介绍图神经网络在知识图谱推理中的应用，并对未来发展方向进行展望。

图神经网络及其在知识图谱中的应用

关键词：图神经网络表达能力知识图谱推理

神经网络——特别是深层神经网络(DNN)，在文本、语音、图像、视频等欧氏空间数据的建模方面取得了很大成功。同时，在欧氏空间数据之外，社交网络、知识图谱、引文网络等以图形式存在的非欧空间数据作为一种常见的数据表示形式也受到了广泛关注。例如，在社交网络中，用户和用户之间通过关注关系构成了复杂的网络连接结构；在蛋白质网络中，氨基酸分子通过结构或距离邻近性构成了网络的连边，刻画了不同蛋白质的特性。近年来，一些研究人员致力于把神经网络模型迁移到图数据这类非欧空间数据上，提出了图神经网络(GNN)模型，成功应用在半监督节点分类、图分类、推荐系统、交通预测、知识推理等任务中^[1]。

在图神经网络模型取得了阶段性成功的同时，研究人员对图神经网络的表达能力及推理能力也产生了极大的兴趣^[2]。应该从哪些理论角度衡量图神经网络的表达能力？图神经网络模型在有效刻画复杂结构关联的同时，具备了怎样的推理能力？如果知识图谱是知识表示的一种广泛形式，能否在知识图谱的基础上，利用图神经网络进行知识的推理或推断，实现人工智能技术从感知到认知的跨越？

围绕以上问题，本文对图神经网络模型及其在知识图谱中的应用展开讨论。

图神经网络模型

近年来，许多研究人员致力于将传统欧氏空间数据上的神经网络模型迁移到图数据的建模中，通过端到端的方式自动学习和提取图数据的特征。其中，图卷积神经网络(GCN)是目前研究中最活跃，也是最基础的一类模型。图卷积神经网络模型主要包括基于卷积定理的谱方法和基于邻居聚合的空间方法两大类。为了学习到图数据的层级结构，也有学者提出了层次化的图神经网络模型，用以刻画图级别的全局特征。

基于卷积定理的图神经网络模型

由于图数据结构的复杂性（比如幂率度分布等），在将图像领域的卷积神经网络迁移到图数据的过程中，无法直接在节点域中定义卷积算子。为此，基于卷积定理的图神经网络模型借助于卷积定理，从谱域定义了图上的卷积神经网络。

卷积定理指出，信号卷积的傅里叶变换等价于信号傅里叶变换的乘积。以图上拉普拉斯矩阵的特征向量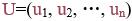图神经网络及其在知识图谱中的应用作为一组基底，对于图上的信号x，傅里叶变换定义为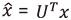，傅里叶逆变换定义为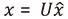^[3]。此时，基于卷积定理，两个图信号x和y的卷积可以定义为：

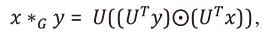
图神经网络及其在知识图谱中的应用

其中*_G表示图卷积算子，⊙表示哈达玛元素积。

布鲁纳(Bruna)等人^[4]用对角参数矩阵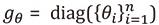图神经网络及其在知识图谱中的应用替换了向量U^Ty，提出了图卷积神经网络的谱方法(Spectral CNN)。该方法的参数复杂度为O(n)，且依赖于拉普拉斯矩阵的特征向量分解，计算复杂度非常高。

为了降低图神经网络的参数复杂度和计算复杂度，德费拉尔(Defferrard)等人^[5]提出了切比雪夫网络(ChebyNet)，通过特征值对角矩阵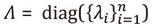图神经网络及其在知识图谱中的应用的多项式展开来近似完全自由的卷积核g。由于涉及到拉普拉斯矩阵的K阶计算，切比雪夫网络的复杂度仍比较高。因此，基普夫(Kipf)等人^[6]进一步将切比雪夫网络简化，提出了图卷积网络模型(GCN)。

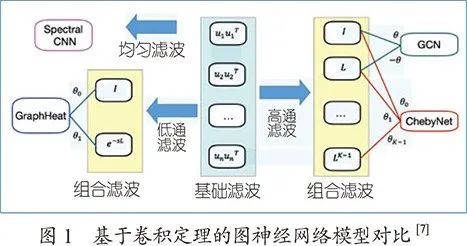
从信号处理的角度来看，切比雪夫网络和图卷积网络均是高通滤波器，为了更好地保留图上平滑信号，徐冰冰等人提出了图热核神经网络模型(GraphHeat)^[7]，利用热核函数参数化卷积核，实现了一个低通滤波器（见图1）。

除了傅里叶变换外，小波变换也提供了一种将信号从节点域变换到谱域的方法，具有基底稀疏、空间局部性以及可以避免高计算代价的拉普拉斯矩阵分解等优点。基于此，徐冰冰等人用小波变换替代了傅里叶变换，提出了小波图神经网络模型^[8]，有效降低了图卷积神经网络的计算复杂度。

在基于卷积定理的图神经网络模型中，切比雪夫网络、图卷积网络以及图热核神经网络等模型虽然都是从谱方法的角度出发的，但其最终形式中已经包含了邻居聚合函数，也被不少人认为是基于邻居聚合的图神经网络模型的特例。本文仅从方法本身的出发点进行归纳，仍将其列为基于卷积定理的图神经网络模型。

基于邻居聚合的图神经网络模型

基于邻居聚合的图神经网络模型旨在从空间域出发，直接通过邻居聚合的机制迭代更新节点的表示，从而定义图上的神经网络模型。这类模型通常由邻居聚合函数、节点更新函数以及读出函数组成[9]。其中，邻居聚合函数迭代地聚合目标节点周围邻居的表示。节点更新函数则根据目标节点上一层的表示以及当前邻居聚合表示，更新节点的表示。当经过K层聚合/更新迭代后，目标节点的表示已经蕴含了其K跳邻居范围的结构信息及特征信息。在这类基于邻居聚合的图神经网络框架下，不同模型的主要区别在于邻居聚合函数和节点更新函数的形式设计。

在池化版本的GraphSAGE^[10]模型中，聚合函数采用了最大值池化以及均值池化形式——将目标节点邻居中表示的最大值或均值作为邻居的聚合，而节点更新函数则选择简单的线性映射函数。在深度卷积神经网络(DCNN)模型^[11]中，聚合函数采用了带权加和的形式，其中权重利用随机行走后得到的K跳转移概率来定义。近年来，注意力机制在各个领域取得广泛成功，有学者提出了图注意力神经网络模型(Graph Attention Network, GAT)^[12]，采用注意力机制来定义聚合函数中的邻居权重，从而更灵活地刻画不同场景下的邻居聚合机制。

随着基于邻居聚合的图神经网络模型的不断发展，研究人员在简单的聚合函数形式外，开始考虑更复杂的图数据建模场景，包括节点表示的置信度^[13]、在建模中引入边上的特征信息^[14]以及搭建高阶结构信息^[15]等。

层次化图神经网络模型

为了更好地学习到图数据的层级结构和全局特征，以应对图级别的挖掘或建模任务，有研究者提出了层次化的图神经网络模型。在这类模型中，最关键的是图粗化的过程，即不断地将相似节点聚类在一起，形成一个新的超节点。超节点的表示由聚类在一起的相似节点共同作用得到，超节点之间的连边由聚类分配矩阵和原邻接矩阵共同作用得到。根据得到节点聚类的方式不同，层次化图神经网络模型可分为预定义和自动学习两类。

Ma等人^[16]提出的EigenPooling模型，利用谱聚类预先定义得到子图的划分，并将同一个子图内的节点表示聚合在一起，形成新的超节点。而Wu等人^[17]则认为度相同的节点具有一定的相似性，提出了度特定的图神经网络模型(DEMO-Net)，将度相同的节点表示聚合在一起，形成新的超节点。

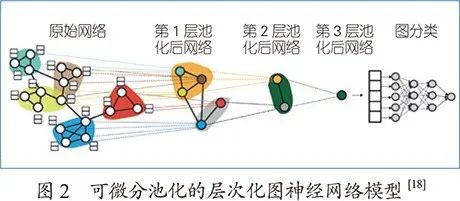
上述层次化图神经网络模型都是通过启发式的方式预先定好节点聚类/图粗化的准则，与真实场景的需求之间存在一定的鸿沟，很难面向各类任务有效提取图数据的特征。为了解决这一问题，Ying等人提出了可微分池化(DiffPool)的层次图神经网络模型^[18]（见图2），通过端到端学习的方式，利用注意力机制自动学习图粗化过程中每层的节点聚类分配矩阵。类似地，阿米尔(Amir)等人^[19]提出了基于记忆层的图神经网络，通过自动学习的方式得到多种分配方式，并利用卷积将多个分配矩阵聚合为一个最终的聚类分配矩阵，用于图的粗化。由于面向任务进行端到端的参数学习，这类基于自动学习的层次化图神经网络，在任务依赖的场景或问题中取得了较好的效果。

图神经网络的表达能力

随着图神经网络模型在许多图数据挖掘任务上取得了经验性成功，越来越多的研究者开始从理论上探讨图神经网络模型的表达能力及其性能上限。

图同构判定

图同构判定问题是判断一对给定的图是否同构。如果两个图是同构的，那么这两个图被认为是等价的，则图神经网络模型应该对其输出相同的表示。因此，我们可以从图同构判定的角度来衡量图神经网络的表达能力，或者说是区分能力。

Weisfeiler-Lehman算法（WL算法）是解决图同构判定的一类算法，具有多个变种，包括1-WL算法、k-WL算法、k-FWL算法等。其中，1-WL算法将图上的每个节点作为对象，根据其邻居信息迭代更新节点的标签。k-WL算法和k-FWL算法均以k-元组作为对象，定义了不同的k-元组邻居来不断更新k-元组的标签。最后通过对比两个图的所有标签判断两个图是否同构。从表达能力来看，k-FWL算法最强，k-WL算法次之，而1-WL算法最弱（如图3所示）。

通过建立WL算法与图神经网络模型之间的关联，可以从理论上给出图神经网络模型表达能力的上界。萨托(Sato)等人^[2]指出，由于现有的图神经网络大多以单个节点作为研究对象，其模型表达能力的上界为1-WL算法。Xu等人^[9]为了使图神经网络模型的表达能力尽可能地接近1-WL算法的上界，构造了一种特殊的单射聚合函数，使其与1-WL算法中标签映射函数的单射性一致，从而达到和1-WL算法相同的表达能力。

为了进一步提升图神经网络的表达能力，有学者提出了高阶图神经网络模型^[15,20]。这类模型以k个节点所组成的k-元组作为超节点，不断地聚合k-元组的邻居信息并进行特征更新，其模型表达能力等价于k-WL算法。需要注意的是，高阶图神经网络模型虽然具备了更强的表达能力，但其计算复杂度也急剧增加。

图同构判定和WL算法为衡量图神经网络的表达能力提供了一个较好的理论框架。但在这个衡量标准下，并不能保证表达能力强的图神经网络模型在非图同构的问题或任务中依然有较好的性能。如何从目标任务的角度衡量图神经网络的表达能力，依然是一个值得探讨的问题。

知识推理

知识推理涵盖了多种不同的任务，例如基于文本的问答、数学推理、视觉智商测试等。严格来说，推理任务需要在给定一组对象集合及答案标签的情况下学习得到一个函数，从而回答关于未知对象集合的问题。根据问题结构的复杂性，可以将推理任务分为四大类^[21]：概要统计(summary statistics)、极值关系(relational argmax)、动态规划(dynamic programming)以及NP-难问题(NP-hard problem)，难易程度依次增加（见图4）。其中，动态规划算法被证明可以解决大多数复杂的推理任务，包括视觉问答、最短路径问答等。

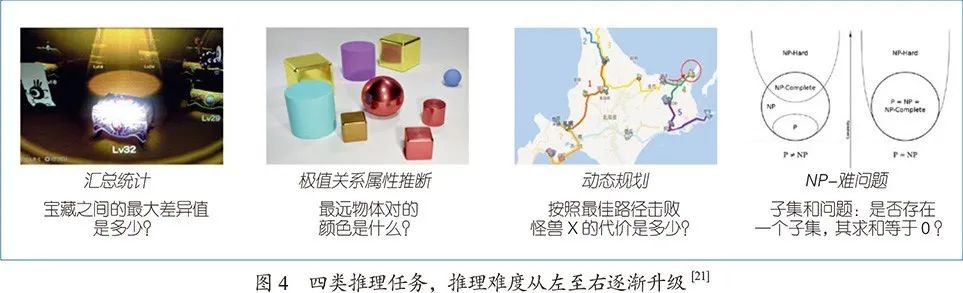
近年来，图神经网络模型在各类知识推理任务中都获得了经验性的成功，但很少有人系统地理解其背后的原因。Xu等人^[21]通过引入算法对齐(algorithmic alignment)策略，将图神经网络与上述四类推理任务的解决算法进行对齐分析，从理论上证明图神经网络模型的推理能力。理论和实验结果表明，多轮迭代的图神经网络模型和动态规划问题可以做到算法对齐，即图神经网络中的节点表示等价于动态规划中子问题的解，而图神经网络中的聚合机制等价于动态规划中的更新策略。因此，图神经网络模型能够有效解决可抽象为动态规划的推理任务（如图5所示）。

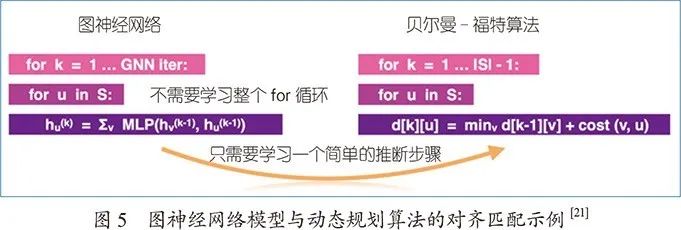
对图神经网络推理能力的理论分析，很好地解释了图神经网络模型在关系推理等应用中被广泛使用的深层原因，也指出了图神经网络模型的局限性（不能解决NP-难的推理问题），为我们更好地应用图神经网络以及设计更好的推理模型提供了指导和借鉴。

图神经网络在知识图谱中的应用

知识图谱本质上是一种语义网络，其节点代表实体，边代表实体之间的各种语义关系。知识图谱推理主要指知识图谱补全或链接预测，旨在给定两个实体，预测它们之间的连边（关系），或者给定头/尾实体和关系，预测尾/头实体。近年来，图神经网络和知识图谱的结合成为解决知识图谱推理的新手段。下面按图神经网络的类型划分简要介绍相关应用。

简单图神经网络的应用

简单图神经网络主要指在图数据上采用多层感知机这类简单神经网络。Xu等人^[22]采用两层简单图神经网络分别进行全局的信息传播和输入依赖的局部信息传播，据此通过一个注意力模块捕捉两类交互，并将最后一步的注意力得分作为概率预测尾实体。该方法可以很好地解释预测。

Du等人^[23]提出CogKR，其模型框架如图6所示，由给定实例之间关系的总结模块和据此推理正确答案的推理模块组成。总结模块采用简单图神经网络结合实体和实体的邻居得到实体的向量表示，推理出实体对的关系。推理模块包括两个迭代的过程，基于总结模块的结果从知识图谱中检索相关信息（系统1），以及在搜集的信息上进行推理（系统2）。这里作者使用一个独特的结构——认知图存储检索信息和推理结果。认知图是知识图谱的一个子集，节点用向量表达。

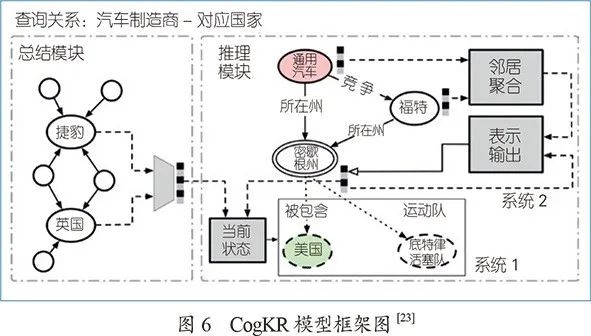
图神经网络在建模的过程中没有显式引入先验逻辑规则，仍需要大量标注样本，为此，Zhang等人^[24]结合简单图神经网络和马尔可夫逻辑网，在马尔可夫逻辑网的变分推理中使用简单图神经网络。该方法可以利用蕴含在逻辑规则中的先验知识和来自图结构数据的监督信息。

图卷积网络的应用

施利克特克鲁尔(Schlichtkrull)等人^[25]提出关系图卷积网络(R-GCN)，首次将图卷积网络扩展到知识图谱推理任务中。R-GCN被用作编码器（见图7），实体与知识图谱中的邻居实体进行关系特定的卷积学习，得到实体的特征向量表示，输入解码器。解码器将头实体向量、关系特定的对角矩阵和尾实体向量的乘积作为得分函数衡量所构成三元组的有效性，由此引入关系向量的建模。

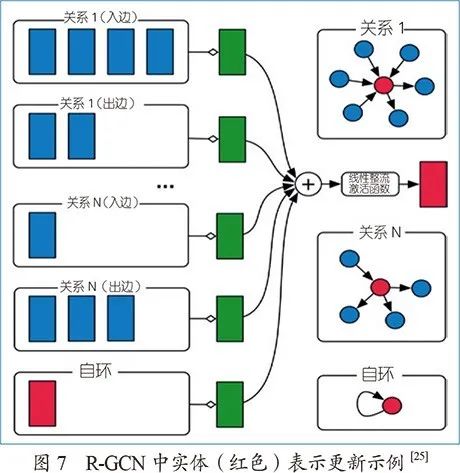
这种将图卷积网络作为编码器，进一步结合得分解码器的做法引起了广泛关注。通常，研究人员采用现有模型的得分函数作为解码器，主要关注对图卷积网络编码器的改进。Shang等人^[26]提出加权图卷积网络(WGCN)，将知识图谱看成多个单关系的子图，每个子图共享相同的卷积操作，但在信息聚合时，引入可学习的关系特定的权重，加权各个子图图卷积的结果。上述方法在图卷积的过程中都没有学习关系的向量表示，为此，Ye等人^[27]和瓦希什(Vashishth)等人^[28]在图卷积的过程中组合连向邻居实体关系的向量表示，将学到的关系向量表示用于解码器。

图注意力网络的应用

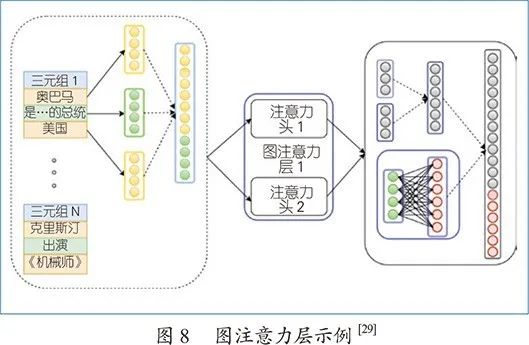
图注意力网络通过引入注意力机制学习邻居的权重，实现更好的邻居聚合。纳撒尼(Nathani)等人^[29]通过关注给定实体多跳邻居内的实体和关系特征，扩展注意力机制到知识图谱，以此作为编码器学习更好的实体和关系向量表示，输入解码器。解码器为现有模型的得分函数。编码器中的一个图注意力层（如图8所示），对于给定实体的每个参与三元组，拼接头尾实体和关系的向量表示，经过变换得到三元组的向量表示，进一步通过多头注意力机制捕捉不同的一跳邻居信息。经由类似的多个图注意力层，可以捕捉多跳邻居信息。

在此基础上，瓦德翰(Vardhan)等人^[30]进一步结合马尔可夫逻辑网，通过期望最大化(Expectation Maximization, EM)算法优化学习。在E步中，通过图注意力网络学习实体和关系的向量表示，并通过解码器（现有模型的得分函数）推理未观察到的三元组；在M步中，基于观察到的三元组和E步中推理得到的三元组，更新马尔可夫逻辑网的权重。最终，将学到的实体和关系向量表示用于推理。

总的来说，图神经网络主要以编码器的形式被广泛应用于知识图谱推理。图神经网络的引入可以更好地捕捉知识图谱中的结构信息，从而提升知识图谱推理的性能。如何同时进行结构信息的捕捉和规则知识的学习，进一步提升知识图谱推理的性能，是未来需要探索的一大问题。

小结

近年来随着深度学习技术的发展，图神经网络模型进入了一个蓬勃发展的阶段。未来，如何借助知识图谱的表示形式，利用图神经网络进行知识的推断或推理，实现人工智能技术从感知到认知的跨越，将是一个很有前景的研究方向。　

致谢：感谢北京智源人工智能研究院和中国科学院王宽诚教育基金的支持。

参考文献

[1] 徐冰冰, 岑科廷, 黄俊杰等.图卷积神经网络综述[J]. 计算机学报. 2020, 43(05): 755-780.

[2] Sato R. A Survey on The Expressive Power of Graph Neural Networks[OL]. arXiv preprint arXiv: 2003.04078. 2020.

[3] Shuman D, Narang S K, Frossard P and et al. The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains[J]. IEEE Signal Processing Magazine, 2013, 30(3):83-98.

[4] Bruna J, Zaremba W, Szlam A and et al. Spectral networks and locally connected networks on graphs[C]//ICLR, 2014.

[5] Defferrard M, Bresson X, Vandergheynst P. Convolutional neural networks on graphs with fast localized spectral filtering[C]//NIPS, 2016: 3844-3852.

[6] Kipf T N, Welling W. Semi-supervised classification with graph convolutional networks [C]//ICLR, 2017.

[7] Xu B B, Shen H W, Cao Q, and et al. Graph convolutional networks using heat kernel for semi-supervised learning[C]//IJCAI, 2019: 1928-1934.

[8] Xu B B, Shen H W, and et al. Graph wavelet neural network[C]//ICLR, 2019.

[9] Xu K, Hu W, Leskovec J and et al. How powerful are graph neural networks?[C]//ICLR, 2019.

[10]Hamilton W, Ying Z， Leskovec J. Inductive representation learning on large graphs[C]//NIPS, 2017: 1024-1034.

[11]Atwod J, Towsley D. Diffusion-convolutional neural networks[C]//NIPS, 2016: 193-201.

[12]Veličković P, Cucurull G, Casanova A and et al. Graph attention networks[C] //ICLR, 2018.

[13]Vashishth S, Yadav P, Bhandari M and et al. Confidence-based graph convolutional networks for semi-supervised learning[C]//Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics, 2019: 1792-1801.

[14]Derr T, Ma Y, Tang J. Signed graph convolutional networks[C]//ICDM, 2018: 929-934.

[15]Morris C, Ritzert M, Fey M and et al. Weisfeiler and leman go neural: Higher-order graph neural networks[C]//AAAI, 2019: 4602-4609.

[16]Ma Y, Wang S, Aggarwal CC, Tang J. Graph convolutional networks with eigenpooling[C]// KDD, 2019: 723-731.

[17] Wu J, He J, Xu J. Demo-net: Degree-specific graph neural networks for node and graph classification[C]//KDD, 2019: 406-415.

[18] Ying Z, You J, Morris C, Ren X, Hamilton W, Leskovec J. Hierarchical graph representation learning with differentiable pooling[C]//NIPS, 2018: 4800-4810.

[19] Amir H, Khasahmadi, Kaveh H, Parsa M, Leo L, Quaid M. Memory-based graph networks[C]// ICLR, 2020.

[20] Maron H, Ben-Hamu H, Serviansky H, Lipman Y. Provably powerful graph networks[C]//NIPS, 2019: 2153-2164.

[21] Xu K, Li J, Zhang M, Du S S, Kawarabayashi K I, Jegelka S. What Can Neural Networks Reason About?[C]//ICLR, 2020.

[22] Xu, X, Feng W, Jiang Y, Xie X, Sun Z, Deng Z H. Dynamically Pruned Message Passing Networks for Large-Scale Knowledge Graph Reasoning[C]//ICLR, 2019.

[23] Du Z, Zhou C, Ding M, Yang H, Tang J. Cognitive knowledge graph reasoning for one-shot relational learning. arXiv preprint arXiv:1906.05489. 2019.

[24] Zhang Y, Chen X, Yang Y, Ramamurthy A, Li B, Qi Y, Song L. Efficient Probabilistic Logic Reasoning with Graph Neural Networks[C]//ICLR, 2020.

[25] Schlichtkrull M, Kipf T N, Bloem P, Van Den Berg R, Titov I, Welling M. Modeling relational data with graph convolutional networks[C]//Proceedings of the European Semantic Web Conference, 2018: 593-607.

[26] Shang C, Tang Y, Huang J, Bi J, He X, Zhou B. End-to-end structure-aware convolutional networks for knowledge base completion[C]//AAAI, 2019: 3060-3067.

[27] Ye R, Li X, Fang Y, Zang H, Wang M. A vectorized relational graph convolutional network for multi-relational network alignment[C]//IJCAI, 2019: 4135-4141.

[28] Vashishth S, Sanyal S, Nitin V, Talukdar P. Composition-based Multi-Relational Graph Convolutional Networks[C]//ICLR, 2019.

[29] Nathani D, Chauhan J, Sharma C, Kaul M. Learning Attention-based Embeddings for Relation Prediction in Knowledge Graphs[C]//ACL, 2019: 4710-4723.

[30] Harsha Vardhan L V, Jia G, Kok S. Probabilistic Logic Graph Attention Networks for Reasoning[C]//WWW, 2020: 669-673.

作者简介