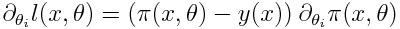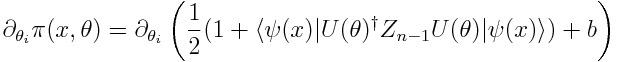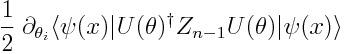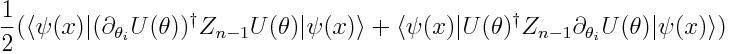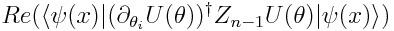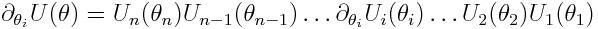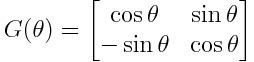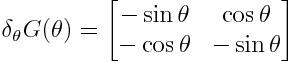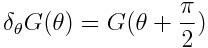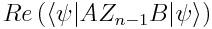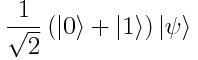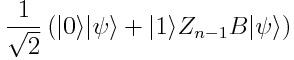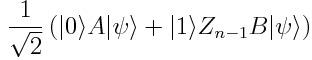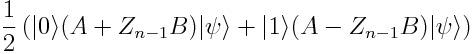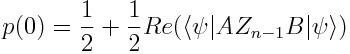教你在经典计算机上搭建一个量子神经网络,已开源 Posted 2021-04-26 AI科技评论
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了教你在经典计算机上搭建一个量子神经网络,已开源相关的知识,希望对你有一定的参考价值。
作者 | Sashwat Anagolum
编译 | 张大倩 、 陈彩娴
本文将教你搭建简单的二分类量子神经网络,并在经典计算机上运行,该项目已经开源。构建量子神经网络与传统的方式并不完全相同——它没有使用带权重和偏置的神经元,而是将输入数据编码为一系列量子比特,应用一系列量子门,并改变门的参数,使损失函数最小化。
项目地址:https://github.com/SashwatAnagolum/DoNew/tree/master/QNN
虽然这听起来很新鲜,但其根本思想和传统还是一样的——改变参数集,使网络预测和输入标签之间的差异最小化,并且同样基于反向传播算法。
接下来,我们首先会介绍传统神经网络的工作原理,如果你对此已经很熟悉,可以直接跳到第3节阅读如何搭建量子神经网络。
权重、偏差和构建模块
几乎人人都知道神经网络。如今,许多酷炫的技术都使用了神经网络,包括自动驾驶汽车、语音助手和恶搞名人照片的软件等。
神经网络与其他算法的不同之处在于:我们不用写下一长串的规则,只需要向神经网络提供数据即可。
我们可以从IRIS数据集中提取一些数据注入神经网络,这些数据包括三种花的信息,然后网络会预测是哪种花。
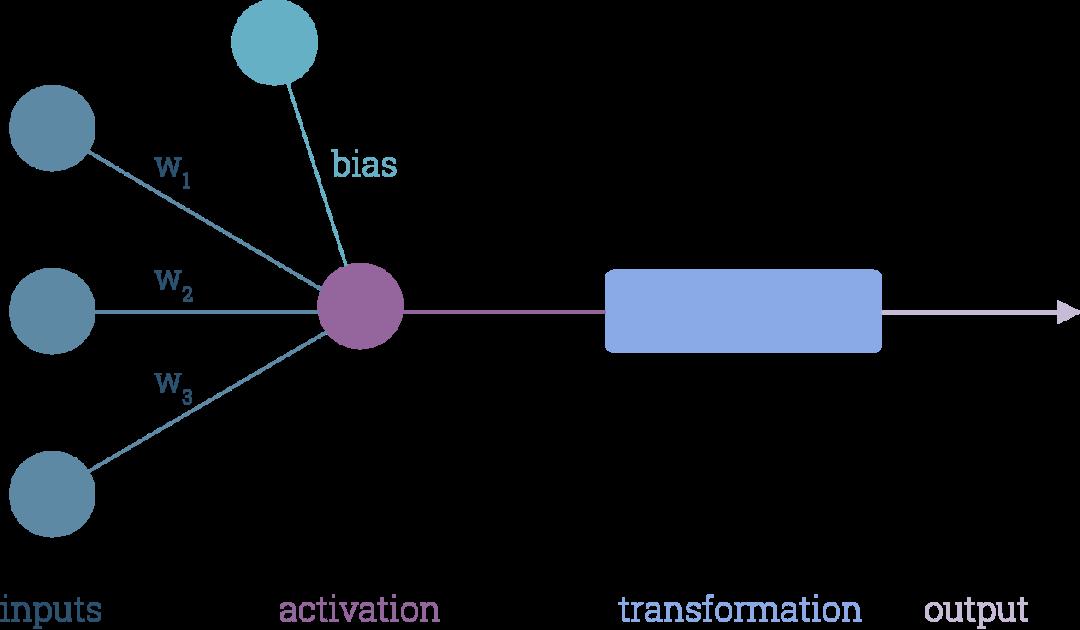
大多神经元会含有多个数字输入(上图的蓝色圆圈),然后将每个输入与表示输入重要性的权重(w_i)相乘。权重越大,相关输入就越重要。
偏差被视为另一种权重,只是它所与之相乘的输入值始终为1。将所有加权输入进行相加后,得到输出值。
然后应用激活函数,我们将得到神经元的激活值,如上图中的紫色圆圈所表示。激活值通过一个函数(上图中的蓝色长方形)传递,输出神经元:
我们可以通过更改激活函数来改变神经元的行为。比方说,我们可以进行一个非常简单的转换,例如:
但实际上,我们应用的是更复杂的函数,例如Sigmoid函数:
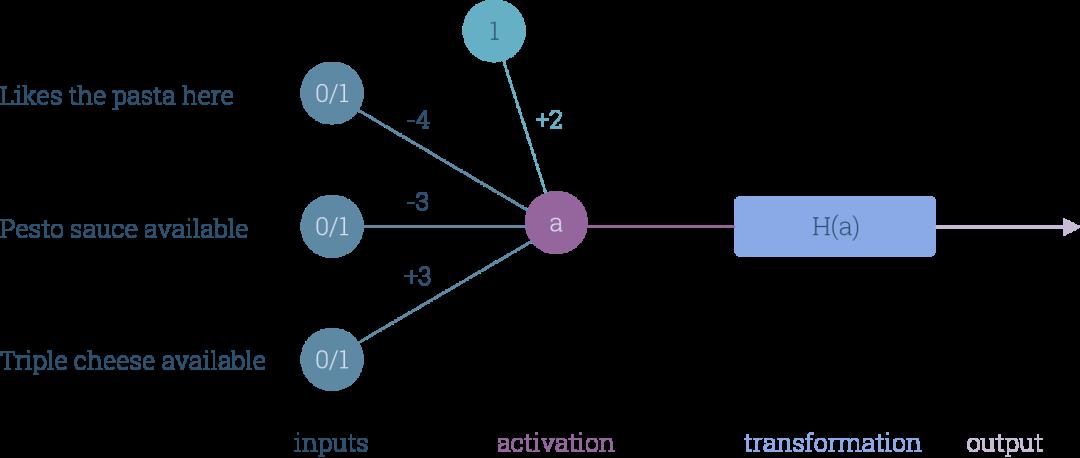
神经元可以根据所接收到的输入来做决策。比方说,我们可以向神经元注入以下三个问题的答案,然后让神经元来猜测我们下次去意大利用餐时是想吃披萨还是想吃意大利面:
问题1:我喜欢这家餐厅的意大利面吗?
问题2:这家餐厅有意大利青酱吗?
问题3:这家餐厅有三层奶酪披萨吗?
抛开可能存在的饮食健康问题不说,我们来看一下神经元会有什么表现:
在对输入进行编码时,我们用0代表“否”,1代表“是”。同样地,对输出进行编码时,我们可以分别用0指代意大利面、用1来指代披萨:
接着,我们用阶跃函数(step function)来转换神经元的激活值:
只需要一个神经元,我们就可以捕捉多种不同的决策行为:
或者换个方式:我们可以对神经元进行编程,让这个神经元与一组特定的偏好对应。
如果我们只是想要预测下次出门吃什么,我们很容易就能找出神经元的一组权重和偏差。但如果我们要在一个规模齐全的网络上进行同样的预测,那该怎么办?
幸运的是,我们不用猜测所需的权重值,只需创建可以改变神经网络参数(比如权重、偏差甚至结构)的算法,以便网络可以学习如何解决问题。
“以退为进”
在理想情况下,神经网络的预测应该与输入关联的标记相同。因此,预测与实际输出的差异越小,神经网络所学到的权重就越优秀。
我们用一个损失函数来量化这种差异。损失函数可以采用任何形式,例如二次损失函数(quadratic loss function):
y(x)是理想输出。当馈送带有参数θ的数据x时,
是神经网络的输出。由于损失始终为非负值,一旦取值接近于0,我们就知道网络已经学会了一个好的参数组。当然,这个过程中可能还会出现其他问题,例如过拟合,但这些可以暂时忽略。
因此,我们要做的不是猜测权重,而是在使用参数θ时,应用梯度下降技术将C最小化:
这时,我们需要留意,增加θ_i的值后,损失会如何变化,然后更新θ_i,以使损失稍微降低。η是一个很小的数字,它的变化取决于我们更新θ_i时所做的改变。
为什么η是一个小的数字呢?因为我们可以对它进行调整,以保证在每次更新后,数据x的损失会接近0。在多数情况下,这并不是一个好的解决方法,因为这虽然可以减少当下x的损失,但其他馈送到网络的数据样本很可能会因此而表现较差。
想必现在大家都已掌握了基本的原理,接下来我们来看看要如何构建一个量子神经网络(quantum neural network)。
量子神经网络工作原理
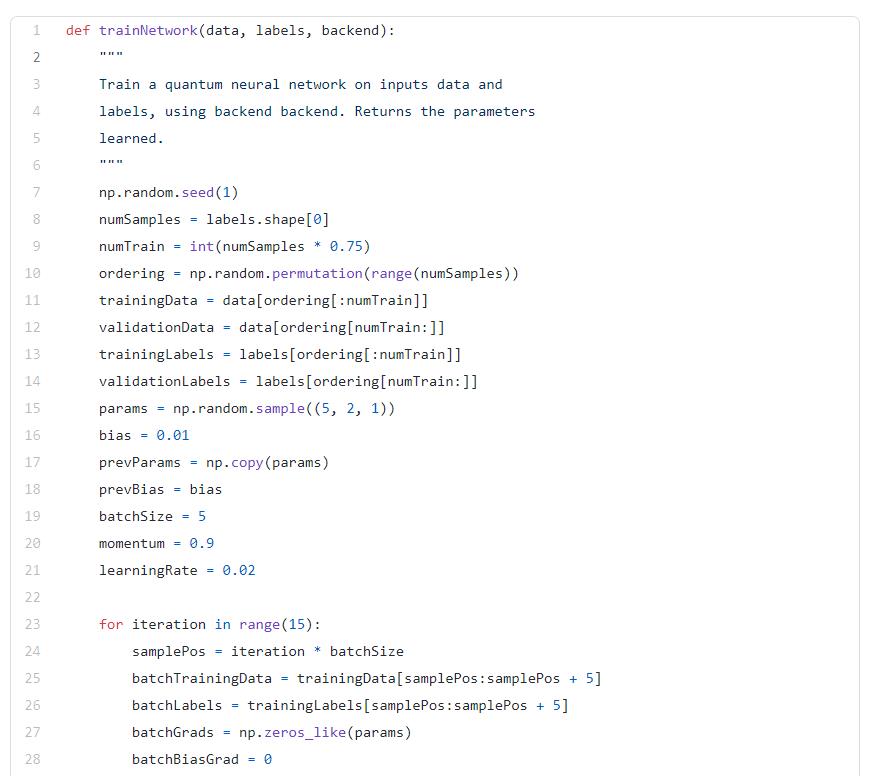
首先,我们向网络提供一些数据x,这些数据x通过特征图传递——通过特征图,我们可以将输入的数据转换成某种形式,从而构建输入量子态:
我们使用的特征图可能是任何形式,比如将一个二维向量x变换成一个角。
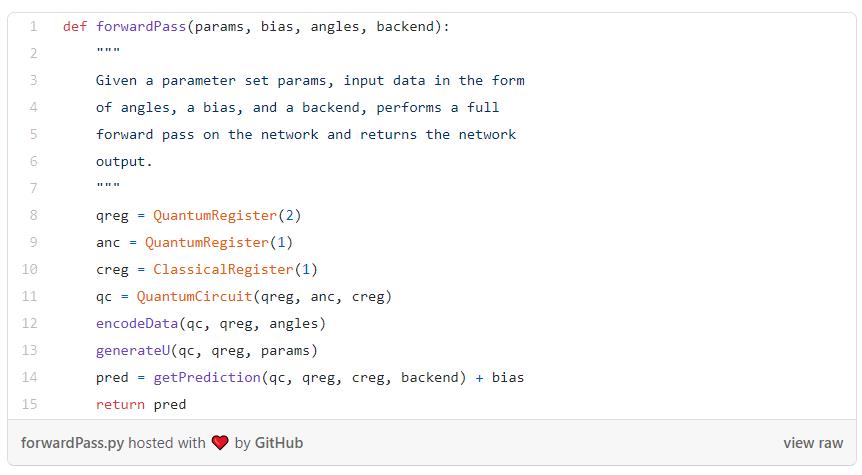
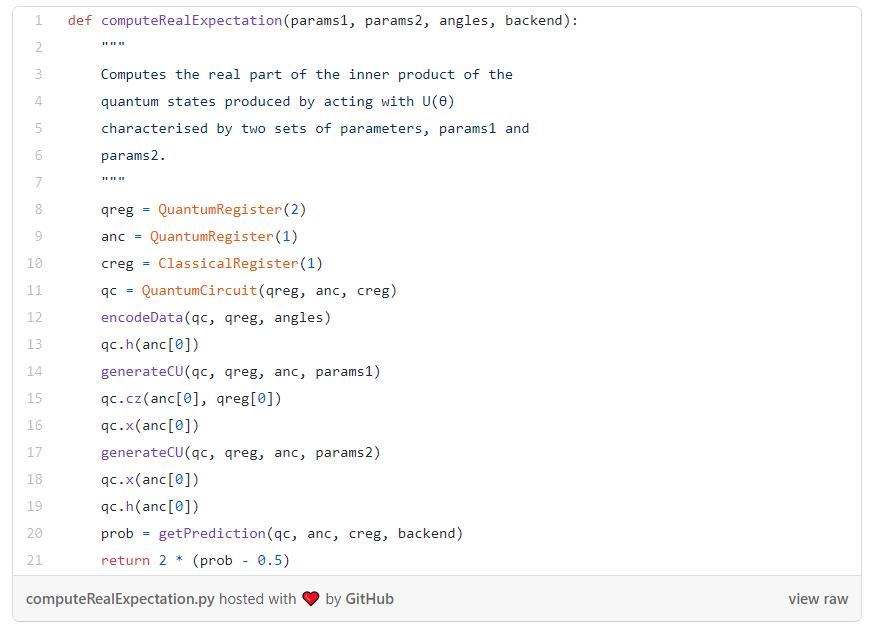
网络的输出,我们称之为π(x,0),是最后一个量子比特被测量为 |1〉状态的概率(Z_n-1代表将Z门应用到最后的量子比特),加上一个经典的偏置项。
最后,我们在输出的数据中取出和 x 有关联的标签,用来计算样本上的损失——我们将使用二次损失,如下:
接下来要计算损失函数
的梯度,当然完全可以使用传统的方法,但我们需要的是一种在量子计算机上计算的方法。
全新的计算梯度的方法
上面这个公式读起来有一点痛苦,但是通过 Hermitian 共轭,可以转化为下面这个简单的公式:
U(θ) 由多个门组成,每一个门又由不同的参数控制,求U的偏导数只需要求门U_i(θ_i)对θ_i的偏导数:
我们把U_i定义为相同的形式,称为G门,当然形式不是唯一的。
所以剩下的就是想办法构造出一个电路来得到所需的内积形式:
Hadamard测试是最简单的方法——首先,我们准备好输入的量子态,并将辅助态制备为叠加态:
现在对|ψ>应用Z_n-1B,约束辅助态是|1>:
因此如果我们用U(θ)代替B,用U(θ)的共轭对θ_i的导数来代替A,然后辅助量子比特为0的概率将会给我们π(x,θ)对θ_i的梯度。
很好!我们找到了一种在量子计算机上解析计算梯度的方法——现在剩下的就是建立我们的量子神经网络了。
建立量子神经网络
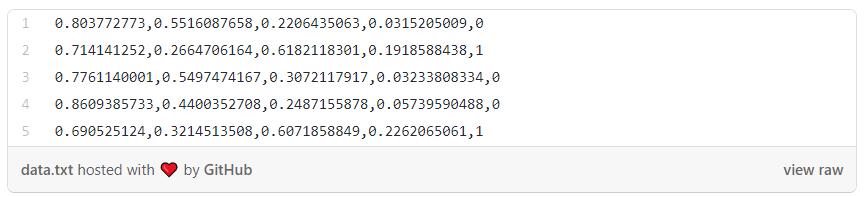
看看我们的数据,这是一版删除了一个类的IRIS数据集:
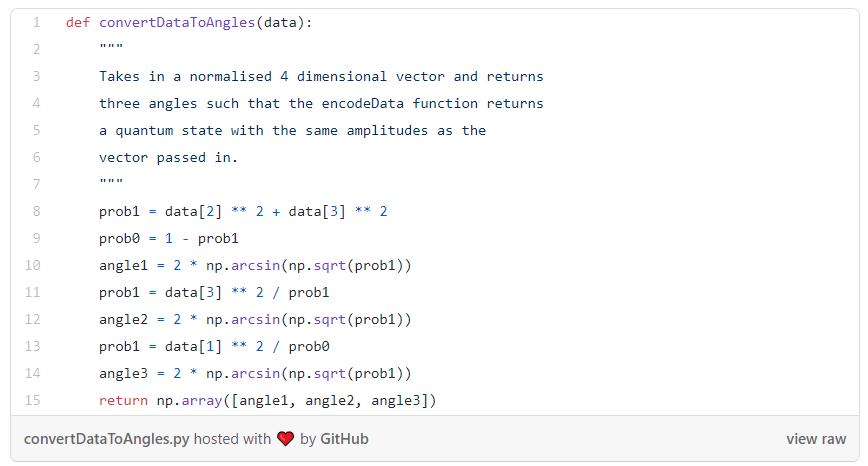
由于输入向量是归一化的,并且是四维的,对于映射有一个超级简单的选择——使用2个量子比特来保存编码的数据,并使用一个映射将输入向量重新创建为量子态。
为此,我们需要两个函数。一个函数从向量中提取角度。
这样讲解可能有点令人困惑,但是你并不一定要理解QNN是如何构建的。如果你想了解构建原理可以阅读这些代码。
代码地址:https://github.com/SashwatAnagolum/launchpad/blob/master/tutorials/load_probability_distributions.ipynb
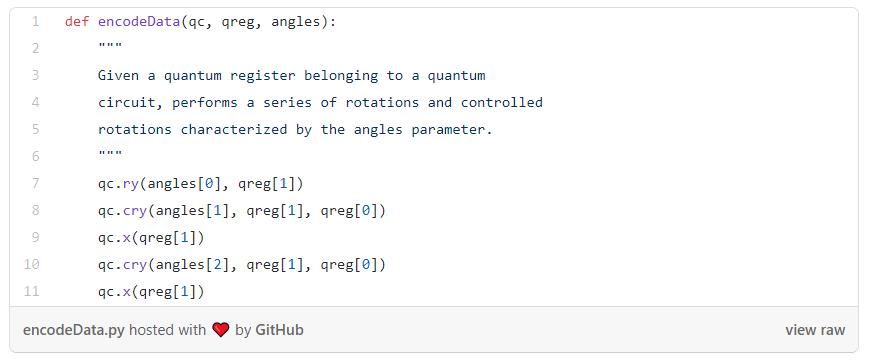
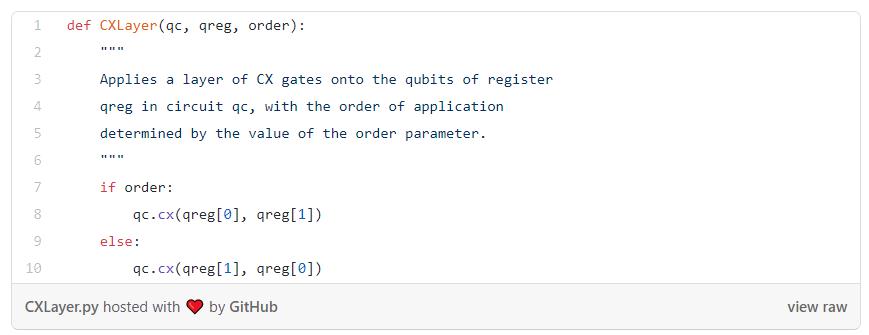
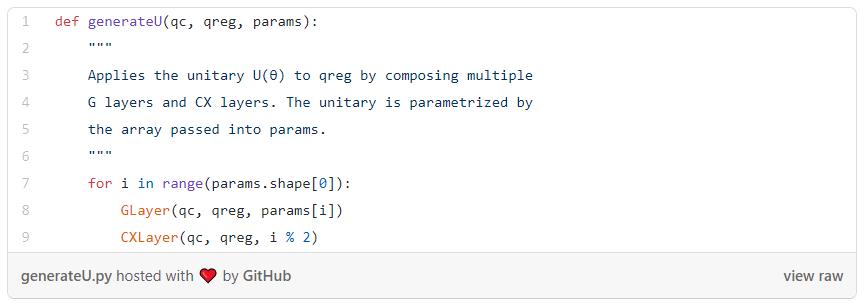
现在可以编写实现U(θ)所需的函数了,我们将采取RY门和CX门交替层的形式来实现函数。
为什么需要CX层?如果不把它们包括进来,就没办法执行纠缠操作,这将限制网络能够涉及的希尔伯特空间的范。使用CX门,网络可以捕捉量子比特之间的交互。
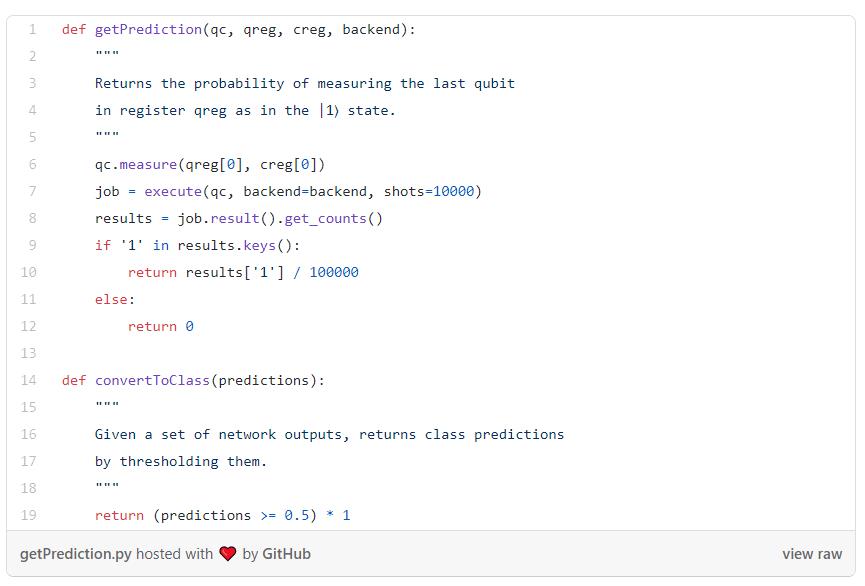
接下来,我们创建一个函数来获取网络的输出,另一个函数将这些输出转换为类别预测:
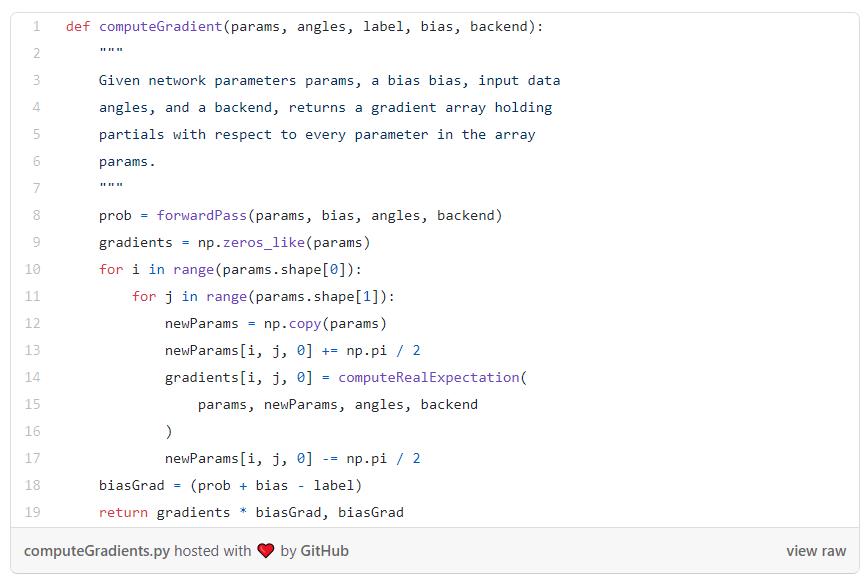
紧接着,需要写出所有关于测量梯度的函数。
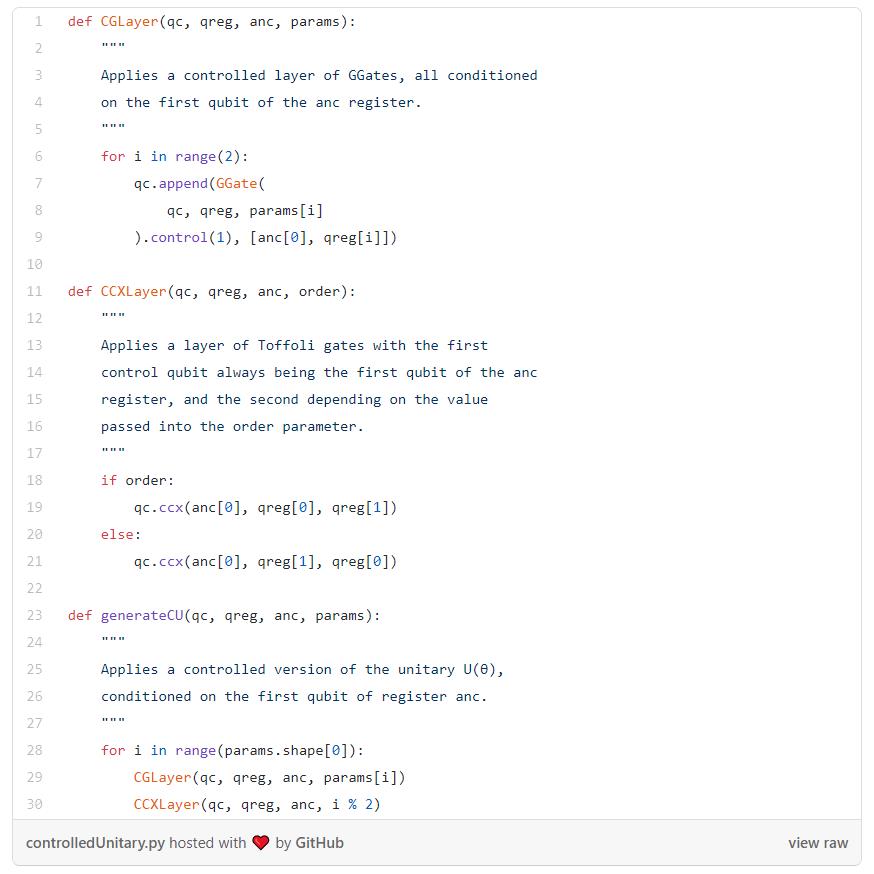
首先,我们必须能够应用控制版本的U(θ):
现在我们可以算出损失函数的梯度,最后做的乘法是为了得到π(x, θ) - y(x) 梯度项:
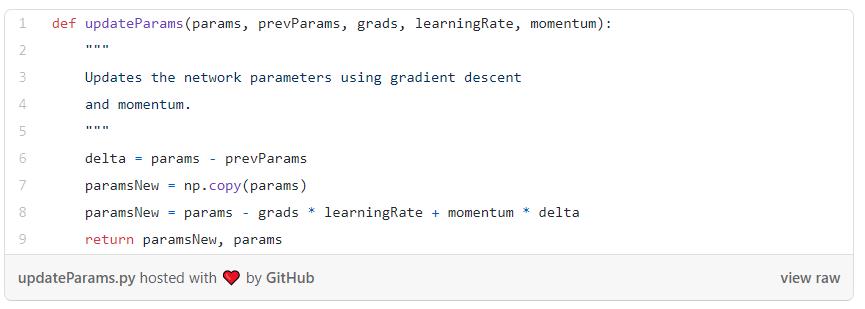
一旦我们有了梯度,就可以使用梯度下降来更新网络参数,“动量”技巧可以帮助加快训练时间:
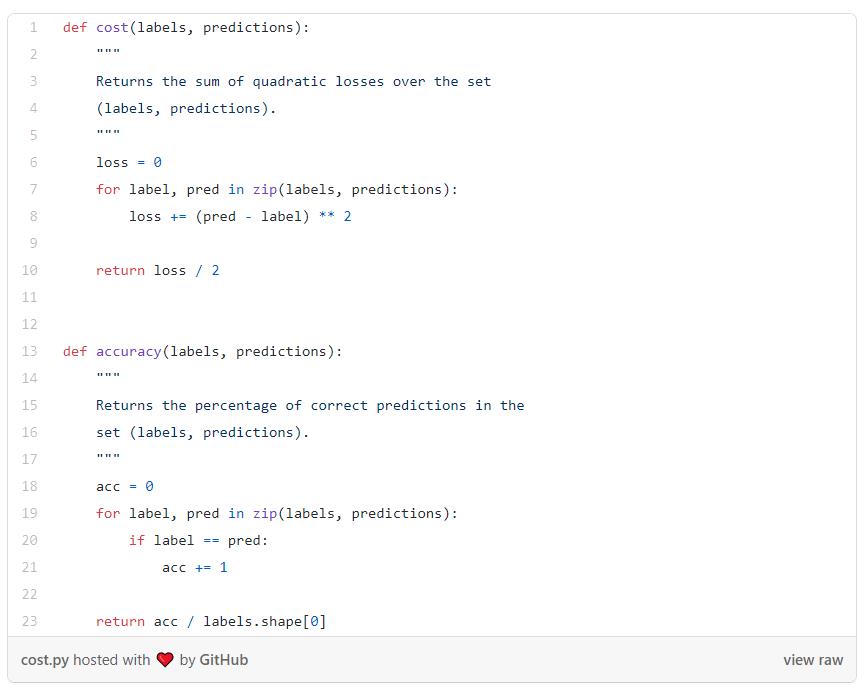
现在我们可以建立自己的损失函数和准确率函数,然后就可以观察网络训练的情况:
我们传递给np.random.sample()方法的数字决定了参数集的大小——第一个数字(5)是G层的数量。
这是我在测试5层网络、15次迭代后得到的数据输出:
这些数据看起来是相当不错——我们在验证集上达到了100%的准确率,这意味着网络成功地覆盖了边缘测试示例!
结语
我们成功建立了量子神经网络,太棒了!可以使用几种方法来进一步降低损失,例如训练网络进行更多的迭代,或者调整超参数:如批量大小和学习率。另一个很酷的方法是为U(θ)尝试选择不同的门。
原文链接: https://towardsdatascience.com/quantum-machine-learning-learning-on-neural-networks-fdc03681aed3
AI科技评论联合博文视点赠送周志华教授“森林树”十五本,在 一文留言区留言,谈一谈你和集成学习有关的学习、竞赛等经历。
AI 科技评论将会在留言区选出15名读者,每人送出《集成学习:基础与算法》一本。
活动规则:
1. 在一文 留言区留言,留言点赞最高的前 15 位读者将获得赠书。获得赠书的读者请联系 AI 科技评论客服(aitechreview)。
2. 留言内容会有筛选,例如“选我上去”等内容将不会被筛选,亦不会中奖。
阅读原文,直达“ KDD”小组,了解更多会议信息!
以上是关于教你在经典计算机上搭建一个量子神经网络,已开源的主要内容,如果未能解决你的问题,请参考以下文章
量子CNN不存在梯度消失问题,物理学家已完成理论证明
从2^N到N^2:量子计算开始助推神经网络!华人学者首次展示量子优势
将量子计算机当作神经网络,首次模拟化学反应,谷歌新研究登上Science封面
手把手教你在Serverless平台上部署应用
量子计算(二十):量子算法简介
量子计算(二十):量子算法简介
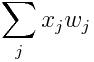
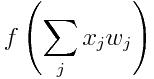
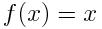
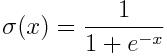
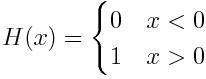
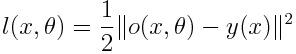
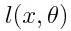 是神经网络的输出。由于损失始终为非负值,一旦取值接近于0,我们就知道网络已经学会了一个好的参数组。当然,这个过程中可能还会出现其他问题,例如过拟合,但这些可以暂时忽略。
是神经网络的输出。由于损失始终为非负值,一旦取值接近于0,我们就知道网络已经学会了一个好的参数组。当然,这个过程中可能还会出现其他问题,例如过拟合,但这些可以暂时忽略。
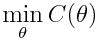
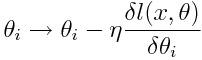
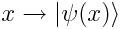
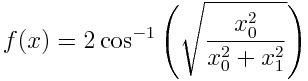
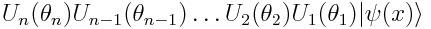
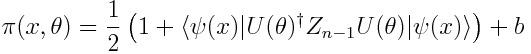
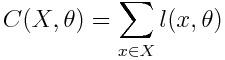
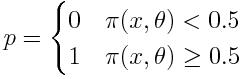
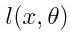 的梯度,当然完全可以使用传统的方法,但我们需要的是一种在量子计算机上计算的方法。
的梯度,当然完全可以使用传统的方法,但我们需要的是一种在量子计算机上计算的方法。