神经网络学习之模拟退火算法

Posted 2021-04-26 小黄有点忙

一、引言

上部分讲到 Hopfield 网络存在的陷入局部最优的解的问题，这主要是因为网络只能严格按照能量函数递减方式演化导致的。那陷入局部最优解是什么意思呢？举个例子，如下图，如果能量函数只能严格减小（通俗讲就是只具备下山能力），则绿色小球将会停止于 A 点，陷入局部最低点，但 A 点并不是我们的全局最小值，那怎么办才能让小球能到达 C 点呢？这时候你可以给能量函数赋予一定的上升能力，通俗讲就是爬山能力。接下来就需要考虑如何令他具有爬山能力，那就是引入概率的因素，对能量函数的演化方向进行调整。如果能量函数能够基于概率出现适当的增长，使其具有爬山能力，则绿色小球可能会走紫色的虚线，适当爬山，有助于小球跳出，停止于 C 点，找到全局最小值，在爬山的过程中，如果增长太厉害，可能会错过全局最小值，如橙色路线，直接越过点 C ，没找到最小值，这就需要设置概率的条件。因此，在该过程中也体现出了随机性。

该思想比较典型的一种算法就是模拟退火算法，接下来介绍一下模拟退火算法。

二、模拟退火算法简介

模拟退火算法(Simulated Annealing，SA)最早是由N. Metropolis等人于1953年提出，由S. Kirkpatrick 等人于1983年成功引入到组合优化领域。

1、什么是模拟退火算法？

模拟退火算法来源于固体退火原理，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。更深入地讲，模拟算法是一种基于概率的算法，该算法从某一较高初温出发，伴随温度参数的不断下降，结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部最优解能概率性地跳出并最终趋于全局最优，因此我们可以称模拟退火算法是一种随机寻优算法。（根据百度百科整理）

讲到这里，我们就能理解为什么模拟退火算法可以引入优化领域，其关键在于物理中固体物质的退火过程与一般组合优化问题之间具的相似性。

2、模拟退火算法的基本原理

模拟退火以状态来接受新状态，假设模型中前一状态为s(n)，系统受到一定的扰动，状态变为s(n+1)，系统的能量也从E(n)变为E(n+1)，定义系统由s(n)变为s(n+1)的接受概率p为：

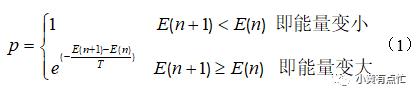
根据表达式（1）可以看出，如果能量变小，即符合我们的能量减小原则，s(n)变为s(n+1)是可以被接受，设其概率为1；如果能量变大，这时候，区别于之前Hopfield里面讲的，这里不会立即抛弃，而是进行概率计算，具体操作如下：首先在[0,1]区间产生一个均匀分布的随机数r，当r<p，s(n)变为s(n+1)是可以被接受，否则就不被接受，保持s(n)。其实此处就体现其随机性。

在式（1）中的以e为底的指数函数中，当温度T越高，幂指数趋于零，概率结果趋于1，这样跳出局部最小值的可能性越大。另一方面，如果温度不变时，能量差越大，幂指数越小，这样概率就会越小，跳出的可能性也就越小。

为了使得模拟退火算法在有限时间内收敛，需要对参数进行适当的调整，从式（1）我们可以看出温度T是关键参数。如果T过大，则消耗的时间会比较长，如果T过小，则退火比较快，可能只达到局部极小值。为了更好地控制参数，我们需要遵循以下几个原则。

（1）初始温度需要足够高，保证所有可能的状态转移都被接受，这样越可能获得高质量的解；

（2）退火速率的规则制定，常见的规则如下；

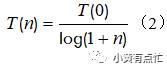
（3）设置退火完成的终止条件，一种是迭代阈值，另一种是在若干次迭代的情况下判断是否没有可以更新的新状态（连续若干个新解都没有被接受）。

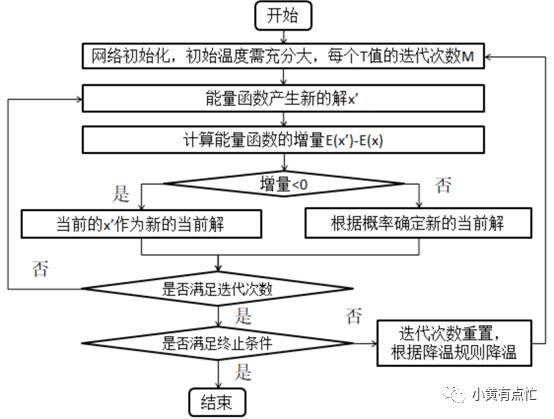
3、模拟退火算法运行流程

如有问题，欢迎交流。