从零开始实现循环神经网络（无框架）

Posted 2021-04-26 比尔的新世界

背景

循环神经网络是深度神经网络的一种，发展于二十世纪八九十年代，随着二十一世纪一零年代后深度学习的复兴，循环神经网络的研究与应用也走上了快车道。循环神经网络主要应用于序列问题，如机器翻译、文本生成、语音识别、股票预测、天气预测等，所谓序列问题指的是问题前后存在紧密关联，前面的一系列信息有助于解决接下去的问题，比如说相声，捧哏说了上一句，逗哏就知道下一句要接啥，比如天气预测，知道了过去几个小时的天气状况，大概就清楚接下来几个小时天气状况如何。循环神经网络从最初的RNN，慢慢发展出LSTM、GRU、BidirectionalRNN、BidirectionalLSTM等种类繁多的算法，各种变形算法可能适用于不同的场景，或者针对某一方面做了优化，如LSTM可以部分解决RNN在长序列问题上容易梯度消失的问题，GRU相对LSTM结构更加简单训练效率更高，但是这些算法本质上都聚焦于“循环“一词，有研究对上千种不同结构的循环神经网络进行了实验，发现这些算法效果上其实差别并不像想象中那么大。本文聚焦于原始的RNN及经典的LSTM网络，从零开始无框架实现RNN和LSTM的前向传播与后向传播，并用于“下个字母”预测问题，希望本文能够加深大家对循环神经网络的理解。

 

解决问题

本文使用的训练数据（部分）如上所示，EOS表示句子结尾，a、b是句子当中可能出现的字母，用UNK来表示未知字母。本文的预测目标为，给定一个新的序列如[a, a, a, a, a]，预测该序列接下来应该出现的字母，直到句子结尾。

 

循环神经网络（Recurrent　Neural　Network）

循环神经网络是深度神经网络的一种，也包括输入层、隐藏层和输出层。一般信息在神经网络当中都是逐层向前传播，循环神经网络的不同之处在于，其输入为序列数据，序列当中当前时刻数据的隐藏层输出会和下一时刻的数据一起作为输入进入同一个隐藏层，是为循环。其结构如下如左所示，如果将循环神经网络隐藏层按序列长度进行展开的话，其结构如下图右所示。

 

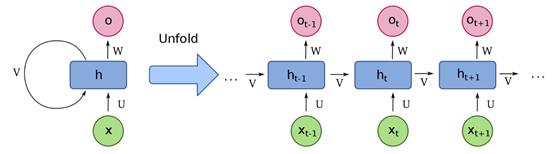
x为序列输入，x =[…, xt-1, xt, xt+1, …]

U 为连接每一时刻输入层与隐藏层的权重矩阵

V为连接上一时刻与下一时刻隐藏层的权重矩阵

U为连接每一时刻隐藏层与输出层的权重矩阵

h为隐藏状态单元

o为输出状态单元

 

对于每一时刻，信息的流动计算公式如下：

ht = f(U xt+ V ht-1)，其中f为激活函数，如tanh

ot =softmax(W ht)

 

接下来我们将开始实现一个RNN网络。

 

参数初始化

首先定义参数矩阵并进行初始化，参数初始化方法对神经网络的训练速度和效果影响很大，本文使用正交初始化方法进行参数初始化，方法详细内容可以参考文末文章链接[1]。

hidden_size = 50 # 隐藏层神经元个数vocab_size = 4 # 词汇表大小def init_orthogonal(param): """ 正交初始化. """ if param.ndim < 2: raise ValueError("参数维度必须大于2.") rows, cols = param.shape new_param = np.random.randn(rows, cols)  if rows < cols: new_param = new_param.T  # QR 矩阵分解， q为正交矩阵，r为上三角矩阵 q, r = np.linalg.qr(new_param) # 让q均匀分布，https://arxiv.org/pdf/math-ph/0609050.pdf d = np.diag(r, 0) ph = np.sign(d) q *= ph if rows < cols: q = q.T new_param = q return new_param
def init_rnn(hidden_size, vocab_size): """ 初始化循环神经网络参数. Args: hidden_size: 隐藏层神经元个数 vocab_size: 词汇表大小 """ # 输入到隐藏层权重矩阵 U = np.zeros((hidden_size, vocab_size)) # 隐藏层到隐藏层权重矩阵 V = np.zeros((hidden_size, hidden_size)) # 隐藏层到输出层权重矩阵 W = np.zeros((vocab_size, hidden_size)) # 隐层bias b_hidden = np.zeros((hidden_size, 1)) # 输出层bias b_out = np.zeros((vocab_size, 1)) # 权重初始化 U = init_orthogonal(U) V = init_orthogonal(V) W = init_orthogonal(W)  return U, V, W, b_hidden, b_out

激活函数

本文使用到的激活函数主要有如下三个：

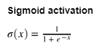
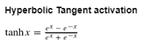
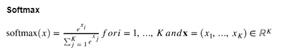
代码实现如下：

def sigmoid(x, derivative=False): """ Args: x: 输入数据x derivative: 如果为True则计算梯度 """ x_safe = x + 1e-12 f = 1 / (1 + np.exp(-x_safe)) if derivative:  return f * (1 - f) else:  return fdef tanh(x, derivative=False): x_safe = x + 1e-12 f = (np.exp(x_safe)-np.exp(-x_safe))/(np.exp(x_safe)+np.exp(-x_safe)) if derivative:  return 1-f**2 else:  return fdef softmax(x, derivative=False): x_safe = x + 1e-12 f = np.exp(x_safe) / np.sum(np.exp(x_safe))  if derivative: pass # 本文不计算softmax函数导数 else:  return f

RNN前向传播

前向传播输入主要有由序列数据组成的输入数据数据及初始化后的网络参数，代码实现如下：

def forward_pass(inputs, hidden_state, params): """ RNN前向传播计算 Args: inputs: 输入序列 hidden_state: 初始化后的隐藏状态参数 params: RNN参数 """ U, V, W, b_hidden, b_out = params outputs, hidden_states = [], []  for t in range(len(inputs)): # 计算隐藏状态 hidden_state = tanh(np.dot(U, inputs[t]) + np.dot(V, hidden_state) + b_hidden) # 计算输出 out = softmax(np.dot(W, hidden_state) + b_out) # 保存中间结果 outputs.append(out) hidden_states.append(hidden_state.copy()) return outputs, hidden_states

RNN后向传播

计算前向传播预测值的相对误差，并按时间从后往前计算网络参数相对于预测误差的梯度，代码如下：

def clip_gradient_norm(grads, max_norm=0.25): """ 梯度剪裁防止梯度爆炸 """  max_norm = float(max_norm) total_norm = 0 for grad in grads: grad_norm = np.sum(np.power(grad, 2)) total_norm += grad_norm total_norm = np.sqrt(total_norm) clip_coef = max_norm / (total_norm + 1e-6) if clip_coef < 1: for grad in grads: grad *= clip_coef return gradsdef backward_pass(inputs, outputs, hidden_states, targets, params): """ 后向传播 Args: inputs: 序列输入 outputs: 输出 hidden_states: 隐藏状态 targets: 预测目标 params: RNN参数 """ U, V, W, b_hidden, b_out = params d_U, d_V, d_W = np.zeros_like(U), np.zeros_like(V), np.zeros_like(W) d_b_hidden, d_b_out = np.zeros_like(b_hidden), np.zeros_like(b_out) # 跟踪隐藏层偏导及损失 d_h_next = np.zeros_like(hidden_states[0]) loss = 0 # 对于输出序列当中每一个元素，反向遍历 s.t. t = N, N-1, ... 1, 0 for t in reversed(range(len(outputs))): # 交叉熵损失 loss += -np.mean(np.log(outputs[t]+1e-12) * targets[t]) # d_loss/d_o d_o = outputs[t].copy() d_o[np.argmax(targets[t])] -= 1  # d_o/d_w d_W += np.dot(d_o, hidden_states[t].T) d_b_out += d_o  # d_o/d_h d_h = np.dot(W.T, d_o) + d_h_next # Backpropagate through non-linearity d_f = tanh(hidden_states[t], derivative=True) * d_h d_b_hidden += d_f  # d_f/d_u d_U += np.dot(d_f, inputs[t].T) # d_f/d_v d_V += np.dot(d_f, hidden_states[t-1].T) d_h_next = np.dot(V.T, d_f) grads = d_U, d_V, d_W, d_b_hidden, d_b_out  # 梯度裁剪 grads = clip_gradient_norm(grads) return loss, grads

梯度优化

各个参数的梯度通过后向传播计算出来后，需要通过优化算法对参数进行更新，本文使用最原始的随机梯度下降算法（SGD， stochastic gradient descent）进行梯度更新，代码如下：

def update_parameters(params, grads, lr=1e-3): # lr， learning rate， 学习率 for param, grad in zip(params, grads): param -= lr * grad return params

梯度爆炸或消失

从上面后向传播的计算过程可以看出来，如果样本序列过长，梯度传播链条也会很长，过大或者过小的梯度在传播过程当中就会出现梯度爆炸或者梯度消失的问题，导致网络没法训练，这其实就是过深的前馈神经网络训练时会遇到的问题。

 

梯度爆炸可能导致梯度出现NaN值，出现NaN值整个网络就直接瘫痪了，因为没法做正常的数学运算了。梯度爆炸可以使用梯度裁剪、权重正则化等手段来进行控制。

 

深度神经网络训练更常遇到的是梯度消失问题，主要因为大部分激活函数的输出及求导值都小于1。梯度消失会导致靠近输入层的参数基本不更新，相当于传播过程当中的某一环断掉了，导致整个更新过程不完整。梯度消失问题，通过使用Relu等激活函数、Batch Normalization、残差网络、预训练模型、门控网络等方法，现在也基本得到了解决，其中的门控网络，包括GRU（Gated Recurrent Unit）以及接下来要介绍的LSTM网络。

 

LSTM网络

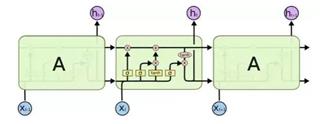
LSTM神经网络在之前  一文中有简单介绍，感兴趣的可以去看看。LSTM按序列长度展开结构如下，可以看出和简单RNN不同之处有二：

一是序列信息往后传递的时候有两条线，上面那条线负责单元状态信息的传递，下面一条则负责隐藏状态信息的传递

二是输入输出隐藏状态之间的转换计算关系更为复杂，接下来将对一个LSTM单元的内部详细结构进行介绍。

 

一个LSTM神经元结构如下：

 

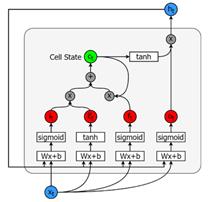
包含5个基本组件，它们是：

• 单元状态（cell state）-储存短期记忆和长期记忆的储存单元

• 隐藏状态(hiddenstate) -根据当前输入、先前的隐藏状态和当前单元状态信息计算得到的输出状态信息

• 输入门（inputgate）-控制从当前输入流到单元状态的信息量

• 遗忘门（forgetgate）-控制当前输入和先前单元状态中有多少信息流入当前单元状态

• 输出门（outputgate）-控制有多少信息从当前单元状态进入隐藏状态

 

计算公式如下：

可以看出，三个门控单元及一个细胞状态单元的输入都是一样的，都是当前时刻的输入xｔ以及上一个隐藏状态ht-1, 但是他们的参数是不同的，同时细胞状态单元使用的是tanh激活函数。遗忘门ft，上一细胞状态ct-1, 记忆门it 及当前细胞状态一起决定输出细胞状态ct， 输出门ot及ct共同决定隐藏状态输出ht。计算公式搞清楚了，下面就可以开始实现LSTM网络了，过程和上面的RNN基本一致。

 

LSTM参数初始化

# 输入单元 + 隐藏单元 拼接后的大小z_size = hidden_size + vocab_size def init_lstm(hidden_size, vocab_size, z_size): """ LSTM网络初始化 Args: hidden_size: 隐藏单元大小 vocab_size: 词汇表大小 z_size: 隐藏单元 + 输入单元大小 """ # 遗忘门参数矩阵及偏置 W_f = np.random.randn(hidden_size, z_size) b_f = np.zeros((hidden_size, 1)) # 记忆门参数矩阵及偏置 W_i = np.random.randn(hidden_size, z_size) b_i = np.zeros((hidden_size, 1)) # 细胞状态参数矩阵及偏置 W_g = np.random.randn(hidden_size, z_size) b_g = np.zeros((hidden_size, 1)) # 输出门参数矩阵及偏置 W_o = np.random.randn(hidden_size, z_size) b_o = np.zeros((hidden_size, 1)) # 连接隐藏单元及输出的参数矩阵及偏置 W_v = np.random.randn(vocab_size, hidden_size) b_v = np.zeros((vocab_size, 1)) # 正交参数初始化 W_f = init_orthogonal(W_f) W_i = init_orthogonal(W_i) W_g = init_orthogonal(W_g) W_o = init_orthogonal(W_o) W_v = init_orthogonal(W_v) return W_f, W_i, W_g, W_o, W_v, b_f, b_i, b_g, b_o, b_v

LSTM前向计算

 

def forward(inputs, h_prev, C_prev, p): """ Arguments: inputs: [..., x, ...], x表示t时刻的数据, x的维度为(n_x, m). h_prev： t-1时刻的隐藏状态数据，维度为 (n_a, m) C_prev： t-1时刻的细胞状态数据，维度为 (n_a, m) p：列表，包含LSTM初始化当中所有参数: W_f： (n_a, n_a + n_x) b_f： (n_a, 1) W_i： (n_a, n_a + n_x) b_i： (n_a, 1) W_g： (n_a, n_a + n_x) b_g： (n_a, 1) W_o： (n_a, n_a + n_x) b_o： (n_a, 1) W_v： (n_v, n_a) b_v： (n_v, 1) Returns: z_s, f_s, i_s, g_s, C_s, o_s, h_s, v_s：每一次前向传播后的中间输出 outputs：t时刻的预估值， 维度为(n_v, m) """ assert h_prev.shape == (hidden_size, 1) assert C_prev.shape == (hidden_size, 1) W_f, W_i, W_g, W_o, W_v, b_f, b_i, b_g, b_o, b_v = p # 保存各个单元的计算输出值 x_s, z_s, f_s, i_s, = [], [] ,[], [] g_s, C_s, o_s, h_s = [], [] ,[], [] v_s, output_s = [], []  h_s.append(h_prev) C_s.append(C_prev) for x in inputs: # 拼接输入及隐藏状态单元数据 z = np.row_stack((h_prev, x)) z_s.append(z) # 遗忘门计算 f = sigmoid(np.dot(W_f, z) + b_f) f_s.append(f) # 输入门计算 i = sigmoid(np.dot(W_i, z) + b_i) i_s.append(i)  # 细胞状态单元计算 g = tanh(np.dot(W_g, z) + b_g) g_s.append(g) # 下一时刻细胞状态计算 C_prev = f * C_prev + i * g  C_s.append(C_prev) # 输出门计算 o = sigmoid(np.dot(W_o, z) + b_o) o_s.append(o) # 隐藏状态单元计算 h_prev = o * tanh(C_prev) h_s.append(h_prev) # 计算预估值 v = np.dot(W_v, h_prev) + b_v v_s.append(v) # softmax转换 output = softmax(v) output_s.append(output) return z_s, f_s, i_s, g_s, C_s, o_s, h_s, v_s, output_s

LSTM后向传播

 

def backward(z, f, i, g, C, o, h, v, outputs, targets, p = params): """ Arguments: z，f，i，g，C，o，h，v，outputs：对应前向传播输出 targets： 目标值 p：W_f，b_f，W_i，b_i，W_g，b_g，W_o，b_o，W_v，b_v， LSTM参数 Returns: loss：交叉熵损失 grads：p中参数的梯度 """ W_f, W_i, W_g, W_o, W_v, b_f, b_i, b_g, b_o, b_v = p # 初始化梯度为0 W_f_d = np.zeros_like(W_f) b_f_d = np.zeros_like(b_f)  W_i_d = np.zeros_like(W_i) b_i_d = np.zeros_like(b_i)
 W_g_d = np.zeros_like(W_g) b_g_d = np.zeros_like(b_g)
 W_o_d = np.zeros_like(W_o) b_o_d = np.zeros_like(b_o)
 W_v_d = np.zeros_like(W_v) b_v_d = np.zeros_like(b_v)  dh_next = np.zeros_like(h[0]) dC_next = np.zeros_like(C[0])  # 记录loss loss = 0 for t in reversed(range(len(outputs))): loss += -np.mean(np.log(outputs[t]) * targets[t]) C_prev= C[t-1] #输出梯度 dv = np.copy(outputs[t]) dv[np.argmax(targets[t])] -= 1 #隐藏单元状态对输出的梯度 W_v_d += np.dot(dv, h[t].T) b_v_d += dv #隐藏单元梯度 dh = np.dot(W_v.T, dv)  dh += dh_next do = dh * tanh(C[t]) do = sigmoid(o[t], derivative=True)*do #输入单元梯度 W_o_d += np.dot(do, z[t].T) b_o_d += do #下一时刻细胞状态梯度 dC = np.copy(dC_next) dC += dh * o[t] * tanh(tanh(C[t]), derivative=True) dg = dC * i[t] dg = tanh(g[t], derivative=True) * dg  # 当前时刻细胞状态梯度 W_g_d += np.dot(dg, z[t].T) b_g_d += dg # 输入单元梯度 di = dC * g[t] di = sigmoid(i[t], True) * di W_i_d += np.dot(di, z[t].T) b_i_d += di # 遗忘单元梯度 df = dC * C_prev df = sigmoid(f[t]) * df W_f_d += np.dot(df, z[t].T) b_f_d += df # 上一时刻隐藏状态及细胞状态梯度 dz = (np.dot(W_f.T, df) + np.dot(W_i.T, di) + np.dot(W_g.T, dg) + np.dot(W_o.T, do)) dh_prev = dz[:hidden_size, :] dC_prev = f[t] * dC grads= W_f_d, W_i_d, W_g_d, W_o_d, W_v_d, b_f_d, b_i_d, b_g_d, b_o_d, b_v_d # 梯度裁剪 grads = clip_gradient_norm(grads) return loss, grads

到目前为止，RNN和LSTM网络的前后向传播都实现完毕，可以看出LSTM参数比RNN要多不少，计算过程也更为复杂。两者的训练过程一致，整个训练过程包括 输入数据->数据预处理->前向传播->后向传播->更新参数，代码如下：

# 遍历训练集当中的序列数据for inputs, targets in training_set: # 对数据进行预处理 inputs_one_hot = one_hot_encode_sequence(inputs, vocab_size) targets_one_hot = one_hot_encode_sequence(targets, vocab_size) # 针对每个训练样本，定义一个隐状态参数 hidden_state = np.zeros_like(hidden_state) # 前向传播 outputs, hidden_states = forward_pass(inputs_one_hot, hidden_state, params) # 后向传播 loss, grads = backward_pass(inputs_one_hot, outputs, hidden_states, targets_one_hot, params) # 梯度更新 params = update_parameters(params, grads, lr=3e-4)

数据处理模块这里就不细讲了，感兴趣的可以到文末代码仓库链接中下载全部代码进行学习。使用LSTM网络训练及验证结果如下：

 

可以看出，LSTM神经网络对这样一个简单的序列预测问题解决得还是可以的，因为这个问题比较简单，规律很好找，比如说四个ａ后面一定跟四个ｂ。对于规律复杂的问题，可能就没这么容易了。有一次有人找我帮忙做一个类似验证码预测（也有可能是六合彩的串码预测）的程序，根据前面多个验证码，预测接下来将会出现的验证码，我试着做了一下，发现训练指标还可以，但是测试指标一塌糊涂，基本等于瞎猜，因为原始问题可能根本就没有规律，所以再厉害的程序也学不到什么东西。

 

总结

• 将循环神经网络展开来看其实和普通的深度神经网络差别不大，特别当将数据序列做成定长样本，同时输入到带残差模块的深度神经网络当中的时候，两者的差别就更小了，可能后者的训练速度及效果还能更有优势。

• LSTM就是一个带有Attention功能RNN，其中几个复杂的门控网络充当加权的作用。

• 循环神经网络当中的循环单元有被更为前沿的attention结构取代的趋势，如当前火热的Transformer。

 

参考

[1] 正交参数初始化：Exactsolutions to the nonlinear dynamics of learning in deep linear neural networks

[2] 代码仓库：https://github.com/hellobilllee/lstm_next_sequence_prediction

[3] A Review of RecurrentNeural Networks: LSTM Cells and Network Architectures