量子计算研究（量子神经网络）

Posted 2021-04-26 GIS花果山

第一篇文章传送门：

第二篇文章传送门：

第三篇文章传送门：

第四篇文章传送门：

第五篇文章传送门：

神经网络主要分为三部分：输入层、隐藏层、输出层。

• 输入层主要将待训练数据加载到RAM中，待进行计算。

• 隐藏层往往具有多层，且上一层与下一层的神经元为全连接模式。

• 输出层主要比较输出结果与实际结果的差值。
  

所以，输入层和输出层（模型调用）适宜采用经典计算；隐藏层和输出层（模型训练）适宜采用量子计算。

针对神经网络，主要的工作分为三类

• 数据加载
  

• 正向传播

• 反向传播

数据加载，适宜加载到经典神经网络的输入层，正向传播和反向传播需要大量的计算，适宜采用量子计算来实施。

正向传播计算：

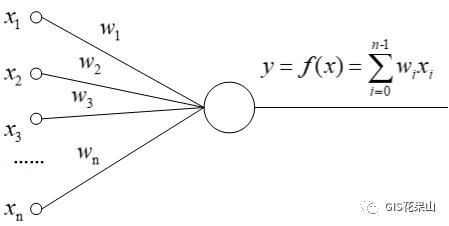
正向传播，采用链式逐神经元计算，最简单的形式可以看成公式y=Ax（为便于理解，不考虑偏置量和激活函数）x代表输入，也是上一层神经元的输出，w代表权重。

反向传播计算：

反向传播，就是通过输出值与实际值的差异来调整权重w的值。简单的形式可以看成公式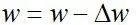

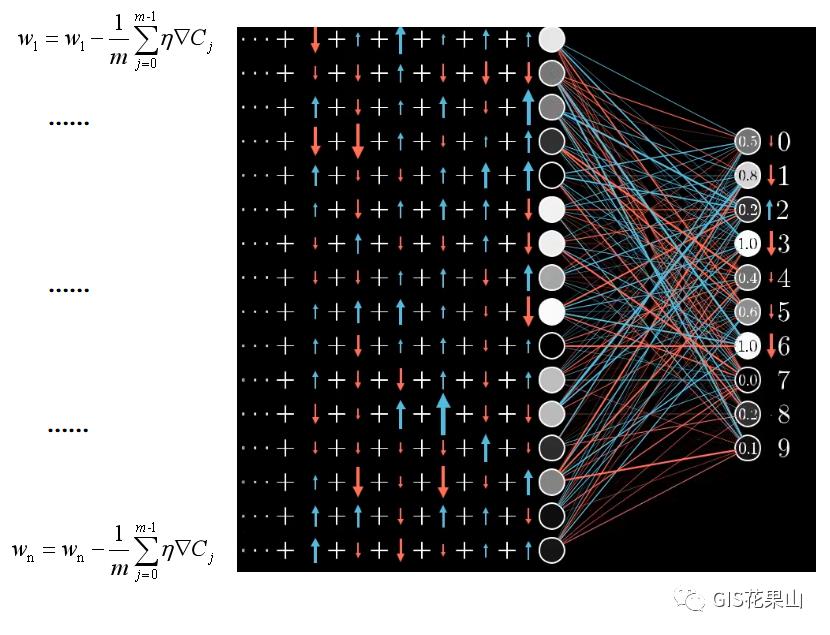
问题聚焦：

神经网络的计算，可以聚焦到下面两个公式：

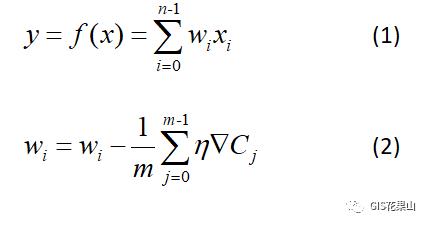
x代表输入，C代表损失函数(Cost)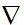，代表梯度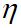，为学习步长。

第一，量子计算用什么算法来实现这两个公式？

第二，在这两个公式的运算上，量子计算能否超越经典计算机？

两个公式都可以转换为Ax+b=y的模式，很容易想到目前的HHL算法（HHL算法主要是为了求解线性方程组 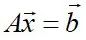，其中矩阵 A和向量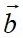已知。HHL算法和QAOA算法常用于量子机器学习，待后续研究）。

至于性能问题，待在真机设备环境下验证，此处不讨论（国内本源量子计划年底推出6量子位真机）。

电路特性：

VQC(Varitional Quantum Circuits)即为量子门组成的权重计算模块。

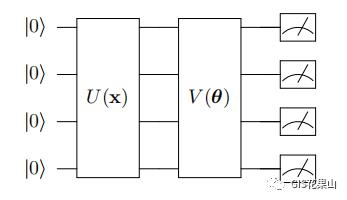
U(x)用于制备量子态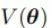，用于梯度优化。

使用参数移位法来推导量子电路的解析梯度。

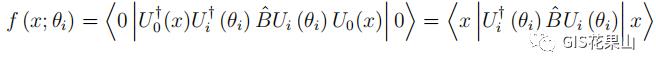
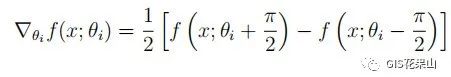
对比一下两种RNN(LSTM)网络的差异：

经典神经网络：

量子神经网络：

本篇文章只是粗略的介绍量子神经网络的结构，细节内容待后续展开。