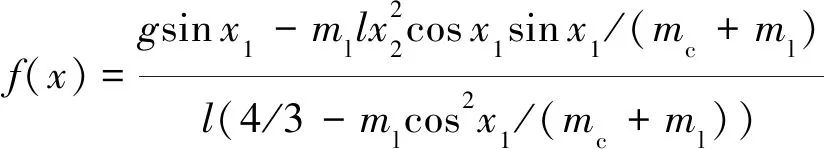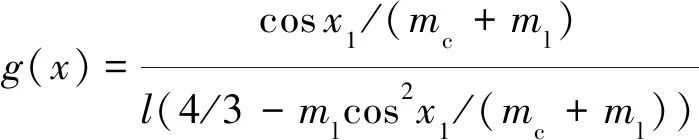差分进化神经网络干扰观测器的设计
Posted 自控中心站
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了差分进化神经网络干扰观测器的设计相关的知识,希望对你有一定的参考价值。
差分进化神经网络干扰观测器的设计
孙明
(江南大学 物联网工程学院)
干扰在控制系统中广泛存在,加大控制难度,会给系统性能带来不利影响,甚至会影响系统的稳定性。摩擦、测量噪声、匹配/未匹配的不确定性、被控对象参数摄动等均会导致控制系统实际的性能或输出偏离期望值,使系统控制效果和精度下降。因此,探寻观测或估计干扰的有效方法,从而抑制或消除扰动成为控制领域的一大热点。RBF神经网络是具有单隐层的3层前馈网络,能以任意精度逼近任意连续非线性函数,且其输入层到隐含层的作用函数是高斯基函数,而隐含层到输出层的映射是线性关系,所以RBF神经网络具有较强的局部逼近能力,在避免局部出现极小值的情况下,兼具加快学习速度的作用,适合对干扰实时估计,满足了系统快速性及自适应性的要求[1]。
文献[2-7]取关于高斯基函数有关的神经网络权值自适应率,得到对外部干扰、模型精确度不足、子系统交叉耦合和内部不确定性组成的复合干扰的逼近,用于设计控制器有关项,可提高系统鲁棒性。自适应率的选取需保证各参数有界,干扰观测误差动态方程特征值趋于无穷大难以实现,导致估计误差收敛范围大于RBF神经网络最佳逼近上界。差分进化(DE)算法通过对父代间差分矢量进行变异、交叉和选择操作,筛选出适应度值更高的新个体,经过有限次迭代运算,优胜劣汰,得到被控对象目标函数的参数最优解[8]。本文结合文献[3]和文献[7],采用DE算法以动态方程估计误差为适应度及最小化目标函数,对神经网络权值在线全局优化,将全局极值作为干扰观测器参数,用于逼近等效干扰。仿真结果表明:该方法显著简化了观测器的设计过程,有效地减小了估计误差。
1 神经网络干扰观测器设计
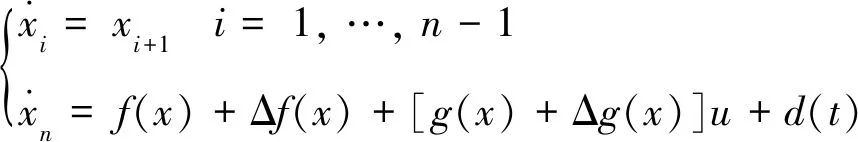
(1)
式中: xi∈R——系统可测状态,i=1, 2, …, n;f(x), g(x)——非线性函数;Δf(x), Δg(x), d(t)——分别为匹配或未匹配不确定性、参数摄动、外界干扰;u∈R——控制输入。

(2)
对于任意x∈M, M为1个闭集区域,定义RBF神经网络最优权值为
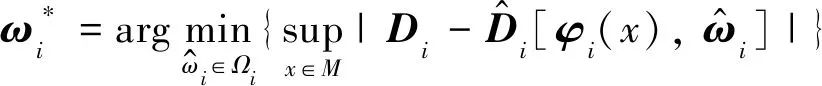
(3)
式中: Ωi——权值可行域,
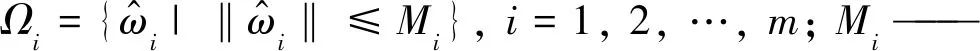 待定参数。
待定参数。
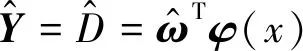
(4)
式中:
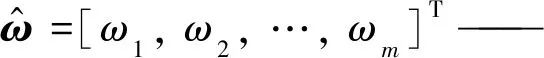 相应隐含层的权值矩阵;φ(x)=[φ1(x), φ2(x), …, φm(x)]T——径向基函数分量组成的向量,且φi(x)=exp(-‖x-ci‖2/
相应隐含层的权值矩阵;φ(x)=[φ1(x), φ2(x), …, φm(x)]T——径向基函数分量组成的向量,且φi(x)=exp(-‖x-ci‖2/
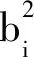 ); ci, bi——分别表示隐含层神经元i的高斯基函数的中心和宽度。
神经网络是万能逼近器,对于给定的足够小逼近误差上界
); ci, bi——分别表示隐含层神经元i的高斯基函数的中心和宽度。
神经网络是万能逼近器,对于给定的足够小逼近误差上界
 复合干扰可表示为
复合干扰可表示为
D(x, t)=ω*Tφ(x)+ε(x)
(5)
式中:
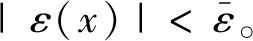
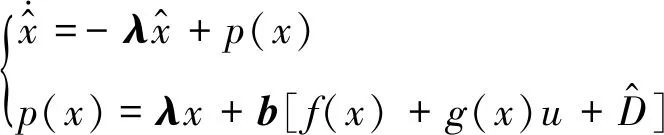
(6)
式中:
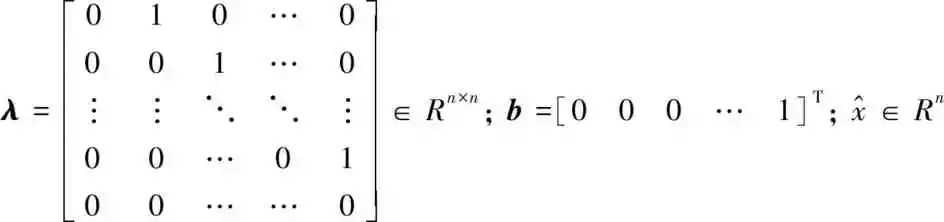 为动态方程状态。
定义动态方程估计被控系统状态误差为
为动态方程状态。
定义动态方程估计被控系统状态误差为
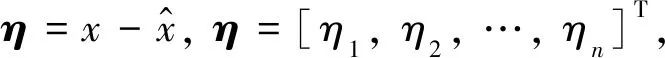 理想权值矩阵与实际权值矩阵误差为
理想权值矩阵与实际权值矩阵误差为
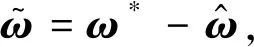 得如下系统状态动态误差方程:
得如下系统状态动态误差方程:

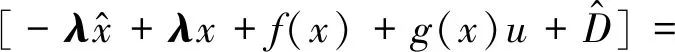

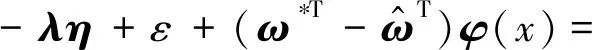
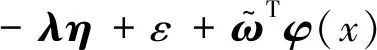
(7)
当η→0且
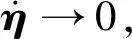 考虑到ε非常小,故神经网络输出
考虑到ε非常小,故神经网络输出
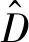 逼近综合干扰D。
逼近综合干扰D。
2 基于神经网络的DE算法设计
DE算法的基本设计思路:随机产生1个初始种群,按照一定规则,将其中任意2个个体的向量差加权与某选定个体进行变异运算,根据目标函数确定适应度值,通过将新个体与该种群个体比较,淘汰适应度值更低的个体,经过有限次更新迭代,搜索全局最优解。上述步骤可概括为:种群初始化、变异、交叉、选择操作。
1) 初始化设置。采用式(8)对种群初始化,生成N个个体:
xi(0)=randi(0, 1)(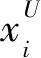 -
-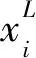 )+
)+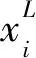
(8)
式中: xi(0)——初代中第i个个体,i=1, 2, …, n, n一般取20~50;
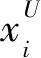 ,
,
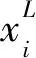 ——对应个体的上下界;randi(0,1)——介于(0, 1)的随机数。
——对应个体的上下界;randi(0,1)——介于(0, 1)的随机数。
2) 变异。取种群中任意3个个体xr1, xr2, xr3;其中r1, r2, r3∈{1, 2, …, N}表示种群个体序数,且r1≠r2≠r3≠i。通过式(9)生成变异个体:
hi(k+1)=xr1(k)+F[xr2(k)-xr3(k)]
(9)
式中: xr2(k)-xr3(k)——差异化向量;F——变异比例因子;k——当前更新迭代次数。变异操作是差分进化算法核心,F的选取影响种群多样性及收敛性,通常F取值为0.2~0.8,最大迭代次数不超过500。
3) 交叉。根据随机概率将种群个体xi与其变异个体hi二项交叉生成新个体:
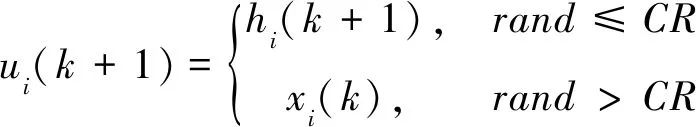
(10)
式中: rand——U[0,1];CR——交叉概率因子,取值为(0.5, 0.9)。
4) 选择。以最小化问题min{f(x), x∈ψ}为例,其中ψ为D维非空有界闭集。将目标函数取为适应度函数,对xi(k)及实验个体ui(k+1)进行适应度值评价,采用如下方法决定两者之一成为下一代成员:
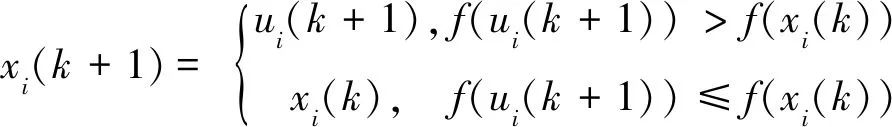
(11)
重复步骤2)至步骤4),直到寻优达到最大迭代次数或满足评价值期望精度[9-10]。
3 仿真实验
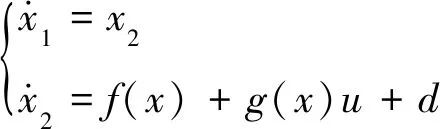
(12)
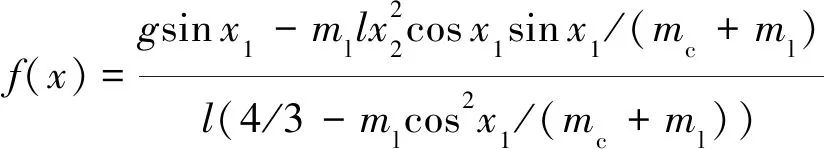
(13)
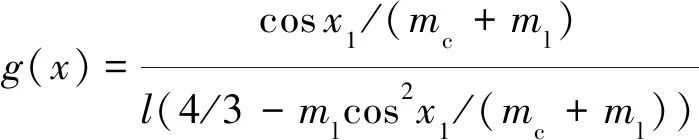
(14)
各参数值分别为: ml=0.1 kg, mc=1 kg, l=0.5 m, g=9.8 m/s2。倒立摆输入作用为u=2sin(2t)+3cos(20*t),等效干扰d=sin(t)+0.5cos(t)+sin(t)*cos(t),神经网络结构为1-5-1,高斯基函数的参数值为c=[-0.5 -0.25 0 0.25 0.5]T, bj=0.2, j=1, 2, 3, 4, 5。选择DE算法对网络权值寻优,范围为ωi∈(0, 5),i =1, 2, 3, 4, 5;种群规模N=40;变异因子F=0.8;交叉因子CR=0.6;最大迭代次数为50。最小化目标函数和适应度函数为
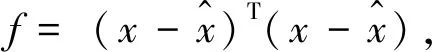 其中
其中
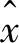 为状态动态系统输出。经过仿真迭代后,可得神经网络最优权值分别为
为状态动态系统输出。经过仿真迭代后,可得神经网络最优权值分别为
 =0,
=0,
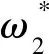 =0.501 3,
=0.501 3,
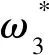 =3.815 4,
=3.815 4,
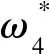 =3.667 0,
=3.667 0,
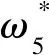 =1.856 7;最小化目标函数值为min f=10.200 5。仿真结果如图1~图8所示。
=1.856 7;最小化目标函数值为min f=10.200 5。仿真结果如图1~图8所示。
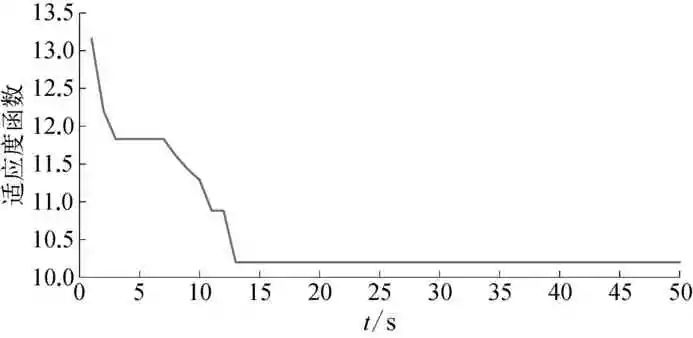
图1 适应度函数迭代变化曲线示意

图2 神经网络权值变化曲线示意
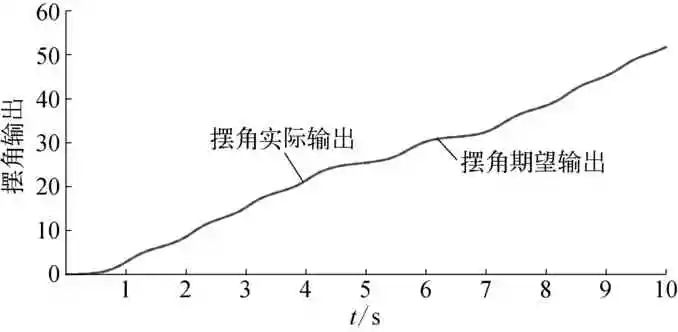
图3 摆角实际输出与期望输出示意
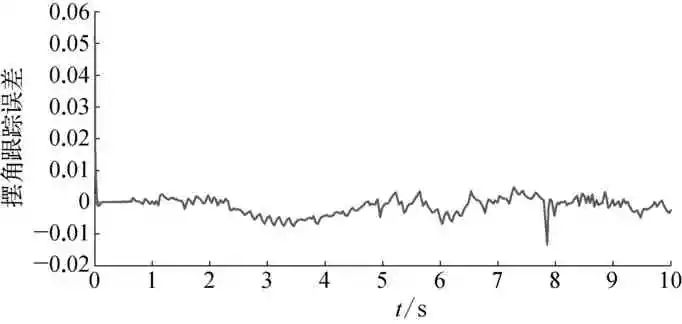
图4 摆角跟踪误差示意
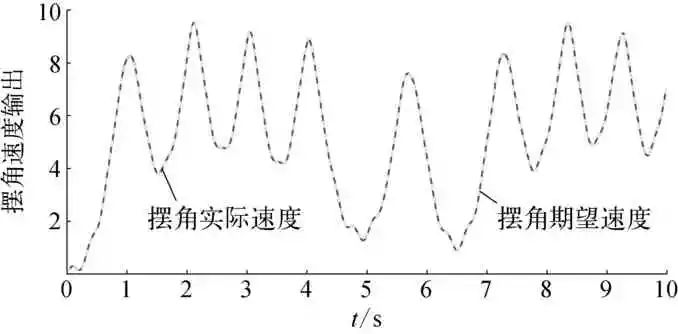
图5 摆角速度实际输出与期望输出示意
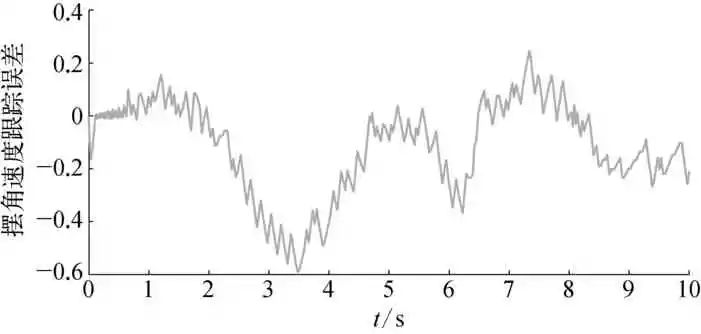
图6 摆角速度跟踪误差示意
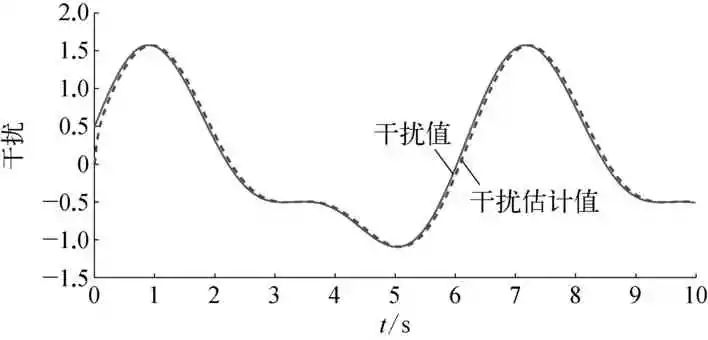
图7 最优权值下的干扰估计示意
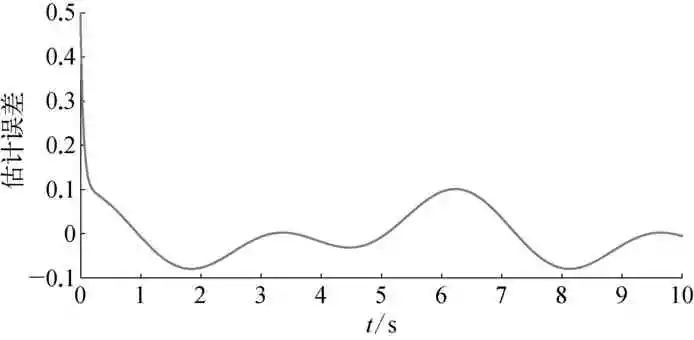
图8 最优权值下的估计误差示意
由图1~图2可知,迭代达到23次左右时,目标函数已达最小,种群寻得全局最优,神经网络各权值获得理想参数值。从图3~图6可看出,被控对象状态动态观测系统能精确逼近摆角及摆角速度变化,各逼近误差较小。图7与图8为最优权值下神经网络干扰观测器对复合干扰的估计情况,与文献[2]和文献[5]采用自适应率动态调整网络权值相比,引入DE算法的神经网络对综合干扰估计误差得到有效减小。
4 结束语
本文针对不确定非线性系统,基于神经网络设计非线性干扰观测器,以被控对象状态动态观测系统对状态逼近最小化为目标函数,采用DE算法通过初始化种群及变异、交叉、选择操作运算后在线动态调整神经网络输出权值,将最优参数用于观测器估计干扰。仿真结果表明:差分进化神经网络干扰观测器能以较高精度逼近外界干扰,有效地避免了参数设置和整定的盲目性,对被控对象参数摄动具有较高的抗扰能力,对于实际工程系统设计具有重大指导意义。
关注方式:
1.扫描二维码
以上是关于差分进化神经网络干扰观测器的设计的主要内容,如果未能解决你的问题,请参考以下文章
差分进化算法
差分进化算法求解函数最优解matlab实现
差分进化算法求解函数最优解matlab实现
差分进化算法求解函数最优解matlab实现
优化预测基于matlab差分进化算法优化BP神经网络预测含Matlab源码 1315期
车载测试系列:CAN协议分层网络
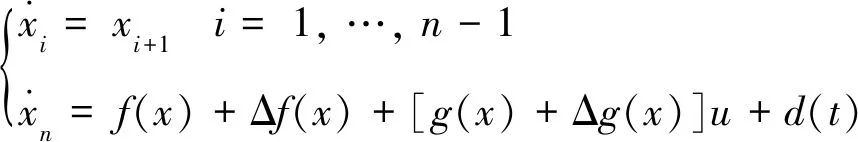
![]()
![]()
![]()
![]()
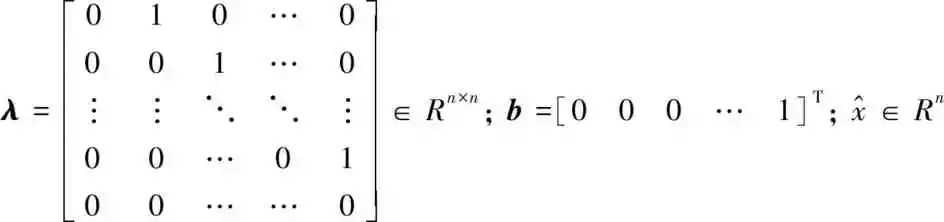 为动态方程状态。
为动态方程状态。
![]()
![]()
![]()
![]()
![]()
![]() -
-![]() )+
)+![]()
![]()
![]()
![]()