团队在使用深度神经网络求随机微分方程的统计解方面取得重要进展！

Posted 2021-04-26 非线性随机动力学

使用深度神经网络求具有α稳定的Lévy噪声的随机微分方程的统计解

引用格式：Zhang H, Xu Y, Li Y, et al. Statistical solution to SDEs with α-stable Lévy noise via deep neural network[J]. International Journal of Dynamics and Control, 2020: 1-12.

      偏微分方程，可以用来描述一个给定系统的基本物理定律，因此在许多学科中扮演着重要的角色。传统上，偏微分方程是基于数学或物理原理推导而成的，例如从量子力学中的薛定谔方程到分子动力学模型，从玻尔兹曼方程到Navier-Stokes方程等。 α稳定的非高斯Lévy噪声的随机微分方程（SDE）是一个有价值的模型，它描述了复杂波动下系统的状况，这种波动已成为物理，化学，生物学领域各种自然系统的关键统计描述符。然而，其分数阶导数的出现导致FFP方程难以求解，并且理论解只能在目前只有少数特殊势函数的情况下获得。因此，用深度学习求FFP方程数值解已变得很流行。

      

      深度学习的模型设计缺少系统指导，大多数深度学习模型都缺少可解释性，这也限制了它的应用。如果加上了微分方程，那么网络架构就是数值微分方程，网络训练就是最优控制，神经网络的设计也就能有理论指导。因此微分方程和深度学习是“天生一对”。为什么深度学习能表示任意函数？万有引力逼近定理发挥了决定性作用。使用深度学习方法求解PDE，在计算数学中是一个新兴的领域。这一新兴领域主要关心的问题在于如何解决高维的问题和更好的处理间断，团队结合了自身研究基础，近期在这一领域有重要进展。以下是文章介绍：

  内容

      针对传统离散格式的网格依赖现象和蒙特卡罗方法的非光滑性，提出了一种利用深层神经网络进行数值求解的新算法。要使用神经网络来求解方程，要依靠准确估计试验解的导数。在整数阶情况下，根据神经网络的逆链规则来近似导数，并可以使用自动微分技术来实现。但是，由于分数阶方程在处理上的空间相关性，自动微分技术无效。因此，有必要设计一种精确估计分数导数的方法。这种“分数中心导数”处理技术非常适合于空间分数阶，并且可以满足计算精度和速度的要求。

      本文在原有DL-FP算法框架下，引入二阶精度的“分数中心导数”方案来逼近Riesz分数阶导数，即求解FFP方程的DL-RFFP算法，该方程主要在空间尺度上考虑，并且该方程的边界条件假定为Dirichlet边界条件，以克服离散方案中的网格依赖现象、蒙特卡罗方法中的非光滑性以及通过梯形估计分数导数时区间的依赖性。此外，文中将方程本身，边界条件和归一化条件作为损失函数，应用L-BFGS-B技术使损失函数最小化。解决了通过深度神经网络进行空间相关性监测和处理的问题，这也是本文的主要创新之处。

      最后本文使用三个示例的数值结果表明了该方法的准确性。数值结果验证了该方法的准确性。与传统的离散格式和蒙特卡罗方法相比，该算法具有网格少、光滑等优点。此外，通过与解析解的比较，本文提出的方法在处理重尾情况方面表现良好。

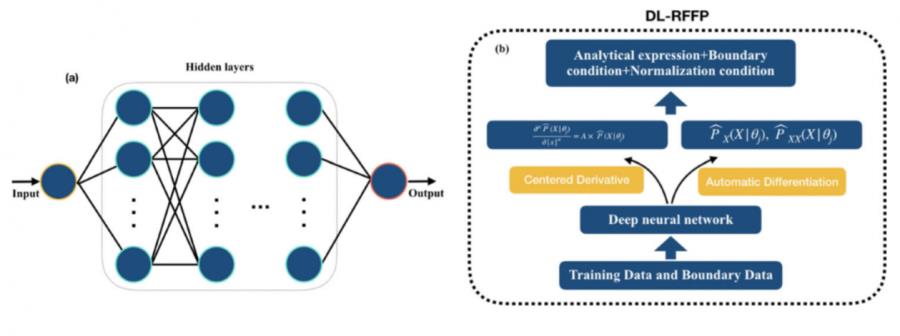
 图1(a) 深度神经网络结构    图1(b) DL-RFFP算法流程

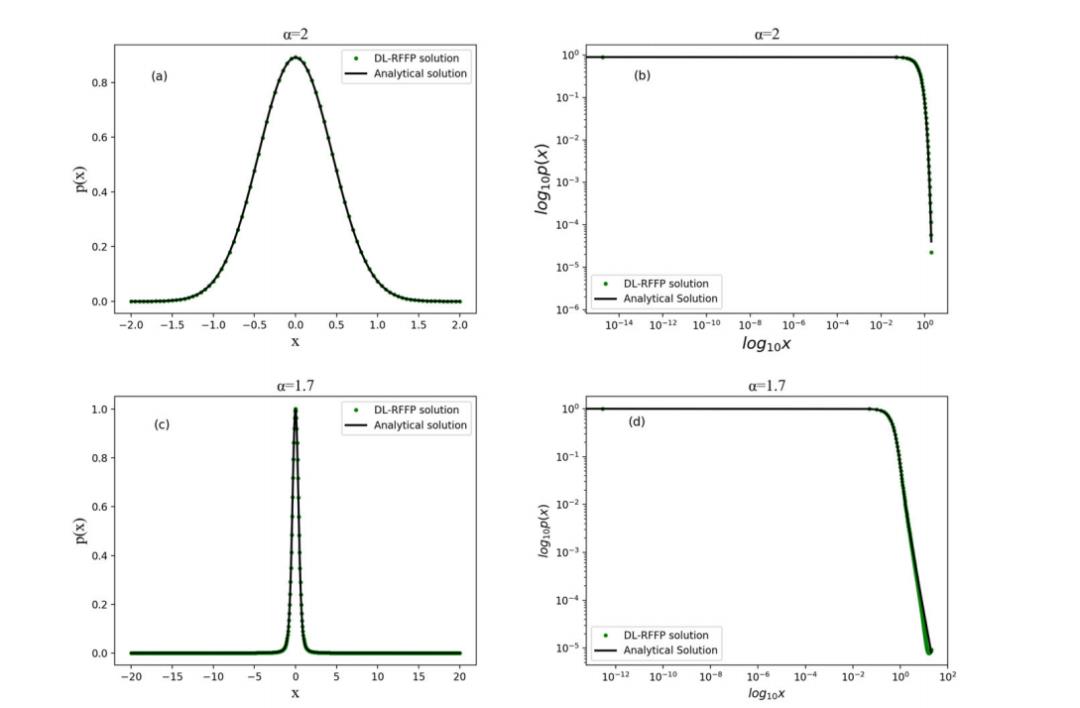图2 DL-RFFP解与精确解的比较结果

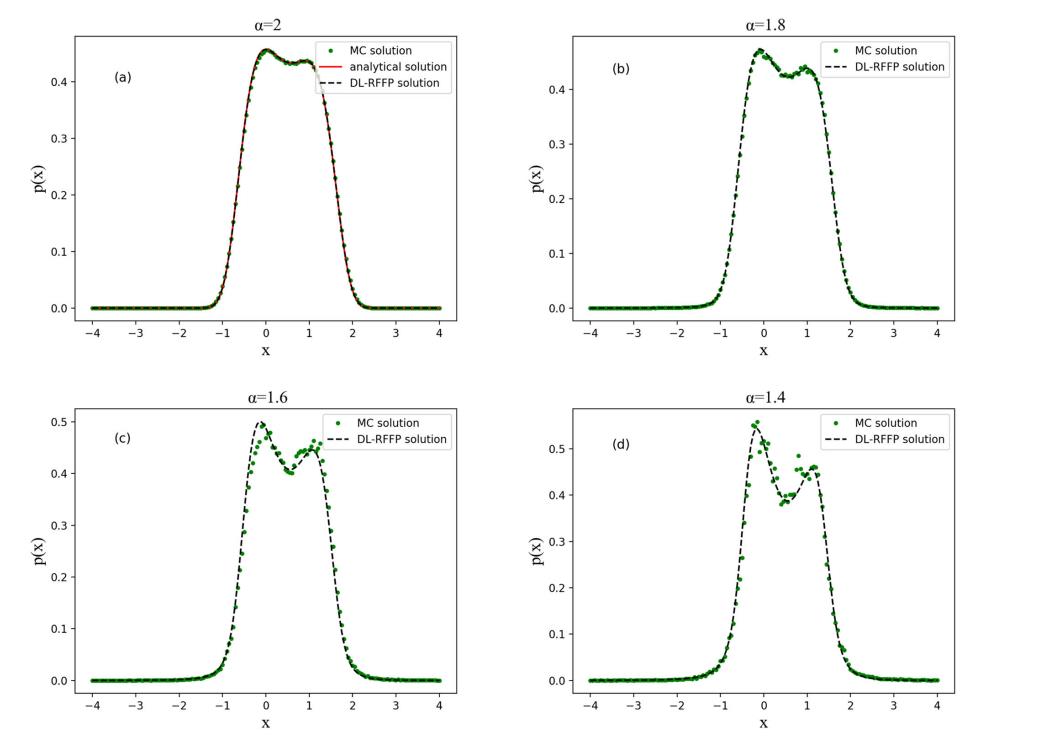
图3 固定噪声强度σ=0.4,系统参数不同时,DL-RFFP算法解与Montecarlo方法解的比较结果

 图4达芬系统中DL-RFFP与Montecarlo解的绝对误差

本文提出的算法在许多不同的领域开辟了新的可能性，在未来，团队研究人员希望将这一模型思想用于解决真实世界中更大规模的问题，包括气候预测、动力学等更高维度的复杂的问题。

文字|张芷昭

排版|孙婷