机器学习实战：GNN（图神经网络）加速器的FPGA解决方案

Posted 2021-04-26 Achronix

应用Achronix Speedster7t FPGA设计高能效、可扩展的GNN加速器

01

概述

得益于大数据的兴起以及算力的快速提升，机器学习技术在近年取得了革命性的发展。在图像分类、语音识别、自然语言处理等机器学习任务中，数据为大小维度确定且排列有序的欧氏（Euclidean）数据。然而，越来越多的现实场景中，数据是以图（Graph）这种复杂的非欧氏数据来表示的。Graph不但包含数据，也包含数据之间的依赖关系，比如社交网络、蛋白质分子结构、电商平台客户数据等等。数据复杂度的提升，对传统的机器学习算法设计以及其实现技术带来了严峻的挑战。在此背景之下，诸多基于Graph的新型机器学习算法—GNN（图神经网络），在学术界和产业界不断的涌现出来。

GNN对算力和存储器的要求非常高，其算法的软件实现方式非常低效，所以业界对GNN的硬件加速有着非常迫切的需求。我们知道传统的CNN（卷积神经网络网络）硬件加速方案已经有非常多的解决方案；但是，GNN的硬件加速尚未得到充分的讨论和研究，在本文撰写之时，Google和百度皆无法搜索到关于GNN硬件加速的中文研究。本文的撰写动机，旨在将国外最新的GNN算法、加速技术研究、以及笔者对GNN的FPGA加速技术的探讨相结合起来，以全景图的形式展现给读者。

2

GNN简介

GNN的架构在宏观层面有着很多与传统CNN类似的地方，比如卷积层、Polling、激活函数、机器学习处理器（MLP）和FC层等等模块，都会在GNN中得以应用。下图展示了一个比较简单的GNN架构。

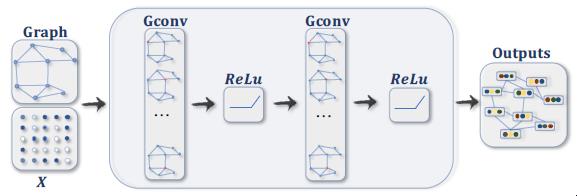
图 1：典型的GNN架构（来源：https://arxiv.org/abs/1901.00596）

但是， GNN中的Graph数据卷积计算与传统CNN中的2D卷积计算是不同的。以图2为例，针对红色目标节点的卷积计算，其过程如下：

• Graph卷积：以邻居函数采样周边节点特征并计算均值，其邻居节点数量不确定且无序（非欧氏数据）。

• 2D卷积：以卷积核采样周边节点特征并计算加权平均值，其邻居节点数量确定且有序（欧氏数据）。
  

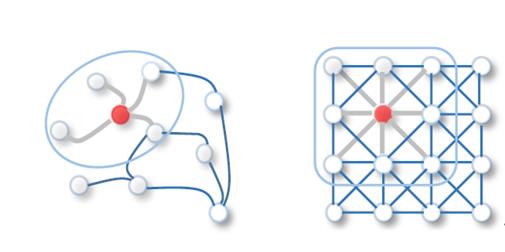
图 2： Graph卷积和2D卷积（来源：https://arxiv.org/abs/1901.00596）

3

GraphSAGE算法简介

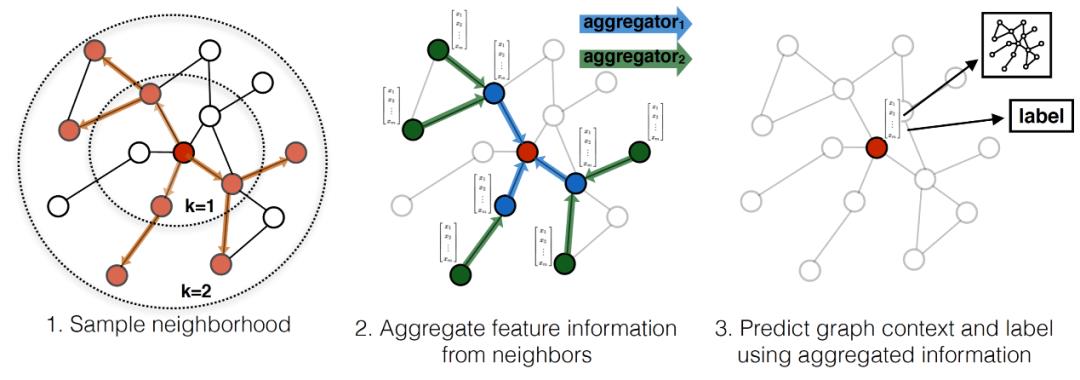
学术界已对GNN算法进行了非常多的研究讨论，并提出了数目可观的创新实现方式。其中，斯坦福大学在2017年提出的GraphSAGE是一种用于预测大型图中动态新增未知节点类型的归纳式表征学习算法，特别针对节点数量巨大、且节点特征丰富的图做了优化。如下图所示，GraphSAGE计算过程可分为三个主要步骤：

图 3：GraphSAGE算法的视觉表述（来源：http://snap.stanford.edu/graphsage）

• 邻节点采样：用于降低复杂度，一般采样2层，每一层采样若干节点
• 聚合：用于生成目标节点的embedding，即graph的低维向量表征
• 预测：将embedding作为全连接层的输入，预测目标节点d的标签

为了在FPGA中实现GraphSAGE算法加速，我们需要知悉其数学模型，以便将算法映射到不同的逻辑模块中。下图所示的代码阐述了本算法的数学过程。

图 4：GraphSAGE算法的数学模型（来源：http://snap.stanford.edu/graphsage）

对于每一个待处理的目标节点x_v，GraphSAGE 执行下列操作：

1）通过邻居采样函数N（v），采样子图(subgraph)中的节点

2）聚合被采样的邻节点特征，聚合函数可以为mean()、lstm()或者 polling()等

3）将聚合结果与上一次迭代的输出表征合并，并以W^k做卷积

4）卷积结果做非线性处理

5）迭代若干次以结束当前第k层所有邻节点的处理

6）将第k层迭代结果做归一化处理

7）迭代若干次以结束所有K层采样深度的处理

8）最终迭代结果z_v即为输入节点x_v的嵌入（embedding）

4

GNN加速器设计挑战

GNN的算法中涉及到大量的矩阵计算和内存访问操作，在传统的x86架构的服务器上运行此算法是非常低效的，表现在速度慢，能耗高等方面。

新型GPU的应用，可以为GNN的运算速度和能效比带来显著收益。然而GPU内存扩展性的短板，使其无法胜任海量节点Graph的处理；GPU的指令执行方式，也造成了计算延迟过大并且不可确定，无法胜任需要实时计算Graph的场景。

如上所述种种设计挑战的存在，使得业界急需一种可以支持高度并发实时计算、巨大内存容量和带宽、以及在数据中心范围可扩展的GNN加速解决方案。

5

GNN加速器的FPGA设计方案

Achronix 公司推出的 Speedster7t系列高性能FPGA，专门针对数据中心和机器学习工作负载进行了优化，消除了CPU、GPU以及传统 FPGA 存在的若干性能瓶颈。Speedster7t FPGA 基于台积电的 7nm FinFET 工艺，其架构采用革命性的新型 2D 片上网络（NoC），独创的机器学习处理器矩阵（MLP），并利用高带宽 GDDR6 控制器、400G 以太网和 PCI Express Gen5 接口，在保障ASIC 级别性能的同时，为用户提供了灵活的硬件可编程能力。下图展示了Speedster7t1500高性能FPGA的架构。

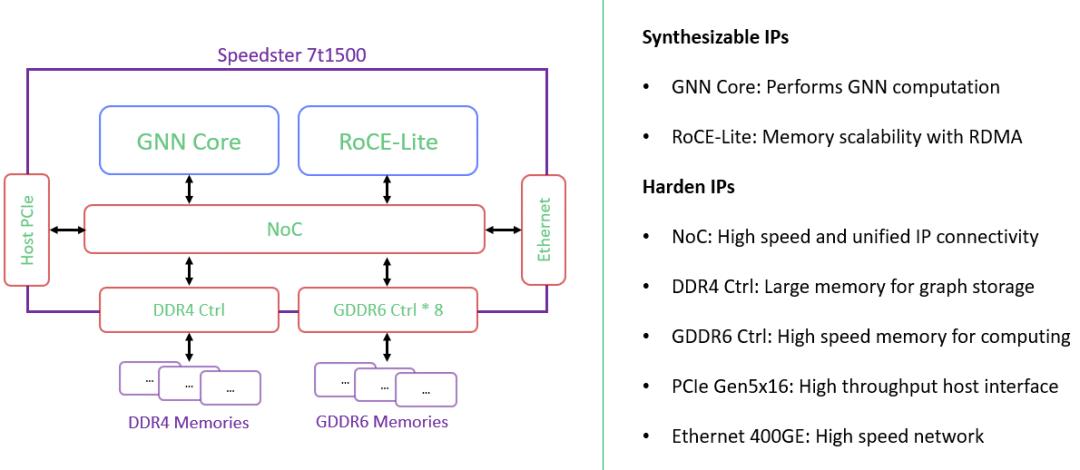
图5: Achronix Speedster7t1500高性能FPGA 架构（来源：http://www.achronix.com）

如上所述种种特性，使得Achronix Speedster7t1500FPGA器件为GNN加速器设计中所面临的各种挑战，提供了完美的解决方案。

表1：GNN设计挑战与Achronix的Speedster7t1500 FPGA解决方案

GNN设计挑战	Speedster7t1500解决方案
高速矩阵运算	MLP机器学习处理器矩阵
高带宽低延迟存储	LRAM+BRAM+GDDR6+DDR4
高并发低延迟计算	FPGA使用可编程逻辑电路，在硬件层面确保低高并发延迟计算
内存扩展	基于4*400Gbps的RDMA，确保在数据中心范围以极低延迟扩展内存访问
算法不断演进	FPGA使用可编程逻辑电路，在硬件层面确保算法可升级重配
设计复杂	丰富的硬IP减少开发时间和复杂度，NoC简化模块间互连并提高时序

5.1 GNN加速器顶层架构

本GNN加速器针对GraphSAGE进行设计，但其架构具有一定的通用性，可以适用于其他类似的GNN算法加速，其顶层架构如下图所示。

图6: GNN加速器顶层架构（来源：Achronix原创）

5.2 GNN Core 微架构

在开始讨论GNN Core 微架构之前，我们先回顾一下本文第3节中的GraphSAGE算法，其内层循环的聚合以及合并（包含卷积）等两个操作占据了算法的绝大部分计算和存储器访问。通过研究，我们得到这两个步骤的特征如下：

表2：GNN算法中聚合与合并操作对比（来源： https://arxiv.org/abs/1908.10834 ）

	聚合操作 （Aggregation）	合并操作 （Combination）
存储器访问模式	间接访问，不规则	直接访问，规则
数据复用	低	高
计算模式	动态，不规则	静态，规则
计算量	低	高
性能瓶颈	存储	计算

可以看出，聚合操作与合并操作，其对计算和存储器访问的需求完全不同。聚合操作中涉及到对邻节点的采样，然而Graph属于非欧氏数据类型，其大小维度不确定且无序，矩阵稀疏，节点位置随机，所以存储器访问不规则并难以复用数据；在合并操作中，其输入数据为聚合结果（节点的低维表征）以及权重矩阵，其大小维度固定，存储位置规则线性，对存储器访问不存在挑战，但是矩阵的计算量非常大。

基于以上分析，我们决定在GNN Core加速器设计中用两种不同的硬件结构来处理聚合操作与合并操作，功能框图如下图所示：

图7: GNN Core功能框图（来源：Achronix原创）

聚合器（Aggregator）：通过SIMD（单指令多数据处理器）阵列来对Graph进行邻居节点采样并进行聚合操作。其中的“单指令”可以预定义为mean()均值计算，或者其他适用的聚合函数；“多数据”则表示单次mean()均值计算中需要多个邻居节点的特征数据作为输入，而这些数据来自于子图采样器（Subgraph Sampler）；SIMD阵列通过调度器Agg Scheduler做负载均衡；子图采样器通过NoC从GDDR6或DDR4读回的邻接矩阵和节点特征数据h⁰_v，分别缓存在Adjacent List Buffer和Node Feature Buffer之中；聚合的结果h^k_N(v)存储在Agg Buffer之中。

合并器（Combinator）：通过脉动矩阵PE来执行聚合结果的卷积操作；卷积核为W^k权重矩阵；卷积结果通过ReLU激活函数做非线性处理，同时也存储在Partial Sum Buffer中以方便下一轮迭代。

合并的结果通过L2BN归一化处理之后，即为最终的节点表征h^k_v。

在比较典型的节点分类预测应用中，该节点表征h^k_v可以通过一个全连接层（FC），以得到该节点的分类标签。此过程属于传统的机器学习处理方法之一，没有在GraphSAGE论文中体现，此设计中也没有包含这个功能。

6

结论

本文深入讨论了GraphSAGE GNN 算法的数学原理，并从多个维度分析了GNN加速器设计中的技术挑战。作者通过分解问题并在架构层面逐一解决的方法，综合运用Achronix Speedster7t1500FPGA所提供的竞争优势，创造了一个性能极佳且高度可扩展的GNN加速解决方案。

如需了解关于Achronix Speedster7t1500FPGA 产品以及该GNN加速器方案的更多信息，请访问Achronix 官方网站：https://www.achronix.com。

作者：袁光 （Kevin Yuan） ， Achronix 资深现场应用工程师

欢迎您扫码关注Achronix微信公众号，了解更多FPGA和eFPGA产品及应用信息：

如需了解更多产品细节，请发送邮件到[e-mail]，或点击“阅读原文”访问Achronix网站以订阅新闻和产品资料，谢谢阅读。