图卷积神经网络：Graph CNN

Posted 2021-04-26 CV学习站

数据可分为两类：Euclidean Data & Non-Euclidean Data。

             

目前在DeepLearning的范畴里，CNN和RNN的世界里，广泛应用的images，sentences，waves，等等，都属于Euclidean data。欧式数据，直观理解为具有工整（栅格化的：grid-like）对称性的数据。然而，网络的概念在现实生活中也是普遍存在的。社交网络，航路网，蛋白质分子联系网等。这些网络常常是不对称的，即每个节点的degree（neighbor数量）是不确定的，数据是不工整的。网络的数学描述是通过图论的理论，即用网络的边和顶点来描述顶点之间的连接关系。

对于euclidean data例如image input，filtering操作是很直观的，是一种按顺序不断重复的convolution计算。而这个顺序，也因由其grid属性，而异常简单。

可是对于graph，无法简单地重复地操作convolution，因为数据的不对称性，滑窗位置的不可重复性。所以，对graph做CNN操作，首先要将不是euclidean的spatial域（顶点域），转换到spectral域（频域）。期待在频域中，非euclidean的事物就变得euclidean了简单说，频域方法的本质动机就是把顶点域的卷积转化为频域里的乘积再求逆傅里叶变换。

一个简单处理图结构的方法：

•       求邻接矩阵A和特征矩阵X

•       串联Xin=[A,X]

•       输入全连接神经网络

             

缺点：

•参数数量过大

•图形变化需重新训练

为什么研究GCN？

1.CNN无法处理Non Euclidean Structure的数据，学术上的表达是传统的离散卷积在Non Euclidean  Structure的数据上无法保持平移不变性。也就是说在拓扑图中每个顶点的相邻顶点数目都可能不同，那么也就无法用一个同样的尺寸的卷积核来进行卷积运算。

2.CNN无法处理Non Euclidean Structure的数据，又希望在拓扑图上有效的提取空间特征来进行学习，所以GCN成为研究重点。

3.数据不是拓扑结构的网络时，也会用到GCN。广义上来讲任何数据在赋范空间内都可以建立拓扑关系，谱聚类就是这样的思想。

 

图卷积网络从卷积方式上可以分为两种：1.谱（spectral）卷积，2.空间域卷积。

谱卷积，即将卷积网络的滤波器与图信号同时搬移到傅里叶域以后进行处理

空间域的卷积，即让图中的节点在空间域中相连、达成层级结构，进而进行卷积。

1. 基于空间域 ：Learning Convolutional Neural Networks for Graphs

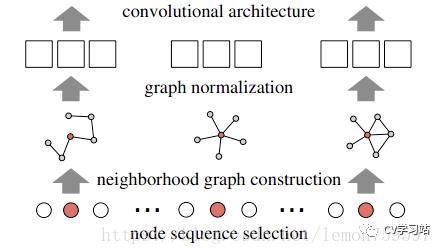
为了能够对任意结构的图进行卷积操作，这篇文章提出了PATCHY-SAN  (Select-Assemble-Normalize)的方法，通过三个步骤构建卷积分片：1.从排序好的图节点中以固定步长选择一个固定长度的节点序列；2.对序列中的每个节点，收集固定大小的邻域集合；3.对由当前节点及其对应的邻域构成的子图进行规范化，作为卷积结构的输入。通过上述三个步骤构建出所有的卷积片之后，利用卷积结构分别对每个分片进行操作。具体示意图如下图所示。

总体上讲，就是用w个固定size=k的子图来表示输入的graph，再将这w个子图正则化后,生成一个w*k维的向量，作为传统的CNN的输入，进行学习。其实就是做了一个从graph到向量的映射的一个预处理过程。

             

具体构建卷积分片的步骤：

1.节点序列选择：为对图中所有的节点进行标号排序，将图中的节点集合根据向心性（节点的度、中心度等）映射为有序的节点序列。从该序列中根据一定的间隔s隔段选取w个节点构成最终的节点序列。

2.邻域节点收集：对于上一步获得的节点序列中的每一个节点，利用广度优化搜索扩展邻域节点，和源节点一起构成一个k大小的邻域集合，搜索到的节点数目大于k,则选取top k,小于k则使用0填充。

3.子图规范化：对邻域集合中的各节点标号排序，得到接受域。那么，对于节点的属性，k个节点属性值构成了一个输入通道，对于边的属性，k^2个属性值也构成了一个输入通道。我们可以分别用一维的卷积层来处理这两种输入通道（对于节点属性卷积层长度为k，对于边属性卷积层长度为k^2）。

For each input graph G, it applies normalized re- ceptive fields for vertices and edges which results in one (w,k,av) and one (w,k,k,ae) tensor. These can be re- shaped to a (wk,av) and a (wk2,ae) tensors. Note that av and ae are the number of input channels

2.基于频域：SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS

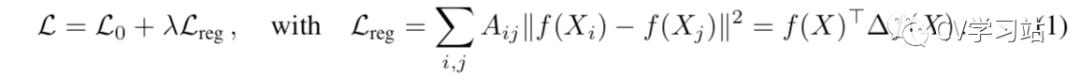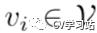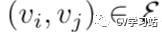基于频域的图卷机依赖在图中相邻的节点更可能包含相同的label这一假设，通过对所有带标签的节点进行监督训练来建模神经网络f(X,A)。其中x是输入数据，包含各节点的特征向量，A为图的邻接矩阵。在损失函数中加入了图的拉普拉斯正则项来约束损失函数，通过图结构数据中部分有标签的节点数据对卷积神经网络结构模型训练，使网络模型对其余无标签的数据进行进一步分类。              描述一个图的数据结构包括点集              ，边集              ，邻接矩阵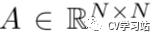              

和节点自由度矩阵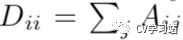              

这篇论文定义来GCN的传播规则

             

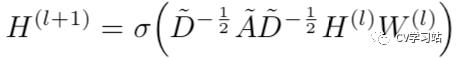
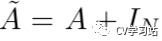             为邻接矩阵加上自连接（即单位矩阵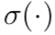），              为定义的relu等激活函数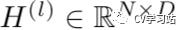，              是第l层的激活值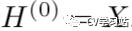，              ，W即为这一层的可训练参数。

 

图谱卷积：

图谱卷积被定义为在傅里叶域中的输入信号与参数化滤波器之间的乘积，公式如下：

             

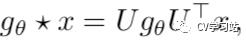
U是归一化图的拉普拉斯矩阵的特征向量

           

      

    

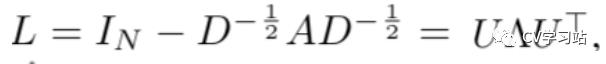
             是由拉普拉斯矩阵的特征值组成的对角矩阵，

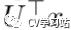             是对x的图傅里叶转换，公式里的              可以认为是L的特征值函数

以上转换方式的缺点就是计算量太大，计算特征向量矩阵U的时间复杂度为 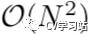             ，而且在对大型图的拉普拉斯矩阵做特征分解的时候消耗更大。

基于此提出了利用切比雪夫多项式K阶截断近似来估计 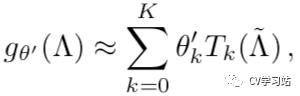             由此定义卷积核。

使用 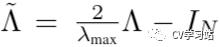             对特征值组成的对角矩阵进行缩放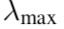，              是L中最大的特征值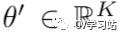，              是切比雪夫系数。

切比雪夫多项式定义为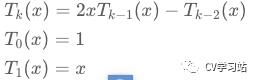              

基于切比雪夫多项式得到的卷积公式为

             

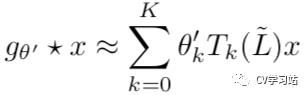
此公式为拉普拉斯算子中的K-阶多项式，即它仅取决于离中央节点最大K步的节点，即K阶图

可以看到该思路与第二代GCN用到的卷积公式非常相似，最终都将参数简化到了K个，并不再需要做特征分解，直接用拉普拉斯矩阵L进行变换，计算复杂性大大降低。

 

             

作者定义了两层GCN的前向传播公式              

使用了交叉熵损失

            

小结

个人认为基于频域的方法更类似于词向量的训练过程，从作者给出的公式也可以看出来将输入特征经过一定的映射关系变为可以决策分类的新的特征向量，每一层GCN可以看做是训练一个大的矩阵来进行这种映射关系，至于论文里作者说的用邻接矩阵加自环当做新的邻接矩阵可用于解决梯度消失/爆炸问题，我也没有搞明白~

基于空间域的方法则比较类似于传统的CNN，传统的CNN卷积也可以看做是固定邻域的GCN，通过将图分解构造为含同样数目节点的子图，利用图的边和点的特征进行卷积。但是两次近似总感觉会丢弃很多信息~